12.11. Третье начало термодинамики

Третье начало термодинамики (или теорема Нернста) было открыто в 1906 г. В. Нернст в процессе термодинамического исследования изменения энтропии химических реакций. Оно тесно связано с поведением теплоемкости при абсолютном нуле температур. Теорема Нернста утверждает, что при приближении к абсолютному нулю энтропия системы также стремится к нулю независимо от того, какие значения принимают все остальные параметры состояния системы:

− (12.11.1)

− третье начало термодинамики.

Поскольку энтропия равна

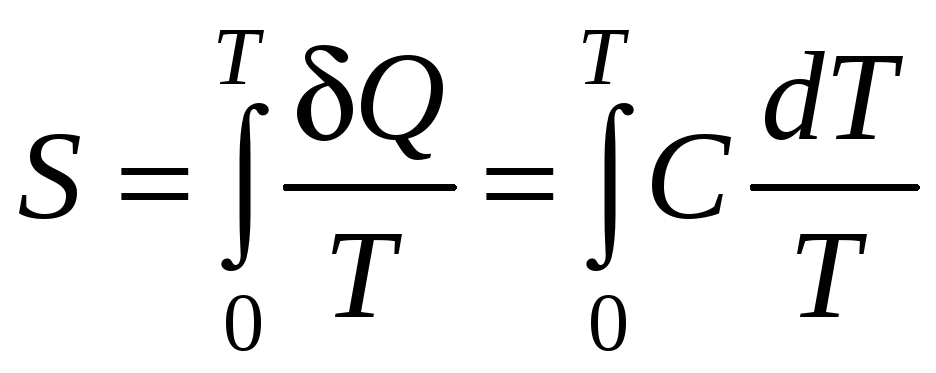, (12.11.2)

а температура Т стремится к нулю, теплоемкость вещества также должна стремиться к нулю, причем быстрее, чем Т. Отсюда следует недостижимость абсолютного нуля температуры при конечной последовательности термодинамических процессов, т. е. конечного числа операций − циклов работы холодильной машины.

Реальные газы и жидкости Лекция № 21

13.1. Уравнение Ван-дер-Ваальса. Изотермы газа Ван-дер-Ваальса.

13.2. Экспериментальные изотермы реального газа.

13.3. Критические параметры и их связь с поправками Ван-дер-Ваальса.

13.1. Уравнение Ван-дер-Ваальса. Изотермы газа Ван-дер-Ваальса.

Экспериментальные и теоретические исследования показывают, что между атомами и молекулами вещества на малых расстояниях действуют силы отталкивания F_o , а на больших − силы притяжения F_п (рис. 13.1.1, а). Эти силы являются результатом квантовомеханического взаимодействия элементарных частиц (электронов, протонов), из которых состоят эти атомы или молекулы. В случае простых неполярных веществ притяжение в основном обусловлено взаимодействием наведенных дипольных моментов молекул. Эти сравнительно слабые ван-дер-ваальсовы силы зависят от расстояния r между молекулами по степенному закону (F  r⁻ⁿ) и, следовательно, носят короткодействующий характер. Область их действия порядка 10⁻⁹ м, т. е. на расстояниях, больших нм, эти силы практически равны нулю. Переход от отталкивания на малых расстояниях к притяжению на больших расстояниях способствует появлению минимума на кривой зависимости потенциальной энергии W взаимодействия двух частиц от расстояния r между ними (рис. 13.1.1, б). На расстоянии r₀ , которое соответствует минимуму потенциальной энергии, сила взаимодействия F обращается в нуль. Положение минимума определяет равновесное расстояние для системы из двух частиц. Для двух молекул простых веществ явный вид потенциальной энергии Ф(r) взаимодействия, которое описывается потенциалом Леннарда − Джонса, имеет вид

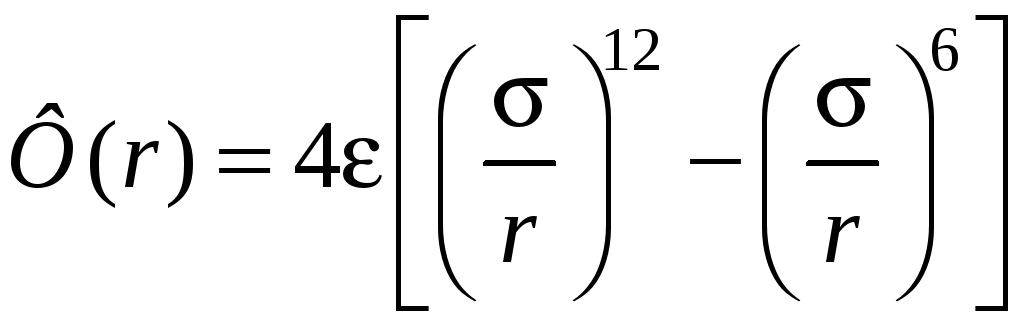. (13.11)

Значения величин  и , которые являются параметрами этого потенциала, можно определить в результате обработки экспериментальных данных о термодинамических свойствах каждого отдельного вещества. Они содержатся в различных справочниках.

Наличие сил притяжения и отталкивания приводит к тому, что при больших давлениях (когда расстояние между молекулами уменьшается) поведение реального газа будет отличаться от модели идеального газа. Одно из наиболее известных приближенных уравнений описывающих состояние реального газа было предложено голландским физиком Ван-дер-Ваальсом. Это уравнение базируется на законе Менделеева − Клапейрона и содержит два параметра (а и b), с помощью которых учитывается вклад сил притяжения на больших расстояниях и сил отталкивания на малых расстояниях между молекулами реального газа.

Силы отталкивания противодействуют проникновению данной частицы в ту область объема сосуда, которая занята другими молекулами. Собственный объем V₀ , занятый частицей, представляется как объем шара с некоторым эффективным диаметром d. Поэтому «свободный объем» V ^*, в котором могут свободно (как в идеальном газе) двигаться молекулы реального газа, будет на некоторую величину меньше, чем объем V, занимаемый газом. «Свободный объем» будет равен

V ^* = V − b, (13.1.2)

где b − поправочный коэффициент для одного моля газа.

Приближенные расчеты показывают, что объем, занятый молекулой, равен учетверенному собственному объему этой молекулы V₀ . Тогда поправка b равна

b = 4N_a V₀ . (13.1.3)

Наличие сил притяжения между молекулами приводит к дополнительному «внутреннему» давлению рⁱ, которое оказывается обратно пропорциональным квадрату V

, (13.1.4)

где a − второй поправочный коэффициент.

В результате внешнее давление р, которое необходимо приложить к реальному газу для удержания его в заданном объеме V, уменьшается по сравнению с давлением р^* в случае идеального газа. Это значит, что

. (13.1.5)

Свободный объем V ^* и давление р^* связаны уравнением Клапейрона − Менделеева

р^* V ^* = RT. (13.1.6)

Подставляя в (13.1.6) выражения (13.1.2) и (13.1.5), получаем приближенное уравнение состояния для реального газа

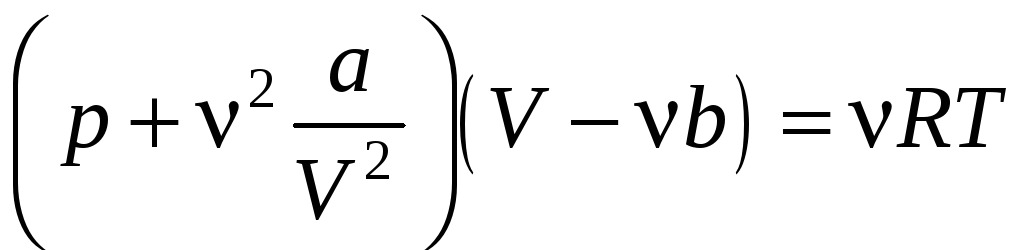. (13.1.7)

Следует отметить, что уравнение Ван-дер-Ваальса лучше согласуется с опытными данными, чем уравнение Клапейрона −Менделеева, особенно при больших давлениях.

Проведем анализ уравнения Ван-дер-Ваальса. С этой целью построим зависимости давления от объема газа при постоянной температуре для нескольких значений температуры (Т₁  Т₂  Т_к  Т₃  Т₄). Результаты представлены на рис. 13.1.2. Полученные кривые − изотермы Ван-дер-Ваальса, оказываются довольно своеобразными: при низких температурах они имеют волнообразные участки (максимумы и минимумы), при некоторой температуре Т_к на изотерме имеется только точка перегиба К, при высоких температурах изотермы Ван-дер-Ваальса похожи на изотермы идеального газа.

С математической точки зрения такой характер изотерм объясняется очень просто. Если привести уравнение Ван-дер-Ваальса к нормальному виду, то оно окажется кубическим уравнением относительно объема V. Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный корень и два мнимых. Очевидно, что первому случаю соответствуют изотермы при низких температурах (три значения объема газа , , отвечают одному значению давления p₁), а второму случаю − изотермы при высоких температурах (одно значение объема V₄ отвечает одному значению давления р₄) (рис. 13.1.2).