
- •7. Элементы релятивистской механики Лекция № 12
- •7.6. Импульс в релятивистской механике
- •7.7. Релятивистские законы Ньютона
- •7.8. Энергия релятивистской частицы. Закон взаимосвязи массы и энергии
- •7.9. Связь между энергией и импульсом частицы
- •8. Элементы квантовой механики Лекция № 13
- •8.1. Корпускулярно-волновой дуализм материи.
- •8.2. Волновые свойства микрочастиц. Опыт Дэвиссона и Джермера
- •8.3. Волновая функция и ее статистический смысл
- •8.4. Уравнение Шредингера
- •Лекция № 14
- •8.6. Волновая функция свободной частицы
- •8.7. Соотношение неопределенностей
- •8.8. Уровни энергии и волновая функция частицы, находящейся в прямоугольной потенциальной яме
- •9.1. Основное уравнение молекулярно-кинетической теории идеального газа
- •9.2. Внутренние степени свободы молекул
- •9.3. Закон распределения энергии молекулы по степеням свободы
- •9.4. Внутренняя энергия идеального газа
- •10. Статистические распределения в молекулярной физике Лекция №16
- •10.1. Понятие статистического распределения, функция распределения. Распределение Максвелла молекул газа по скоростям
- •10.2. Барометрическая формула
- •10.3. Распределение молекул идеального газа во внешнем силовом поле
- •11. Явления переноса Лекция № 17
- •11.1. Явления переноса: диффузия, теплопроводность, внутреннее трение
- •11.2. Длина свободного пробега и среднее число столкновений молекул идеального газа
- •11.3. Коэффициенты переноса для идеального газа
- •12. Основы термодинамики Лекция № 18
- •12.1. Теплота и работа. Первое начало термодинамики
- •12.2. Теплоемкость тела и вещества
- •12.3. Первое начало термодинамики при изохорическом, изобарическом и изотермическом процессах.
- •12.4. Адиабатический процесс. Уравнение Пуассона
- •12.5. Политропические процессы
- •Лекция № 19
- •12.6. Второе начало термодинамики
- •12.7. Обратимые и необратимые термодинамические процессы. Круговой процесс
- •12.8. Тепловые и холодильные машины
- •12.9. Идеальная тепловая машина Карно и ее кпд
- •Лекция № 20
- •12.10. Понятие об энтропии. Статистическое истолкование второго начала термодинамики. Энтропия идеального газа
- •12.11. Третье начало термодинамики
- •Реальные газы и жидкости Лекция № 21
- •13.1. Уравнение Ван-дер-Ваальса. Изотермы газа Ван-дер-Ваальса.
- •13.2. Экспериментальные изотермы реального газа
- •13.3. Критические параметры и их связь с поправками Ван-дер-Ваальса
- •Лекция № 22
- •13.4. Внутренняя энергия реального газа
- •13.5. Эффект Джоуля − Томпсона
7. Элементы релятивистской механики Лекция № 12
7.6. Импульс в релятивистской механике.
7.7. Релятивистские законы Ньютона.
7.8. Энергия релятивистской частицы. Закон взаимосвязи массы и энергии.
7.9. Связь между энергией и импульсом частицы.
7.6. Импульс в релятивистской механике
Принцип относительности СТО предполагает, что все уравнения релятивистской динамики должны быть инвариантными относительно преобразований Лоренца. Поэтому инвариантность формулируемых законов движения в релятивистской механике является определяющим критерием того, что они правильно отражают физическую реальность.
В классической
механике Ньютона импульс определяется
соотношением
![]() .
Требование, что в релятивистской механике
(как и в механике Ньютона) для изолированной
системы тел в любой инерциальной системе
отсчета выполнялся закон сохранения
импульса, и учет законов преобразования
скоростей при переходе из одной системы
отсчета в другую, приводит к тому, что
импульс релятивистской частицы будет
определяться выражением
.
Требование, что в релятивистской механике
(как и в механике Ньютона) для изолированной
системы тел в любой инерциальной системе
отсчета выполнялся закон сохранения
импульса, и учет законов преобразования
скоростей при переходе из одной системы
отсчета в другую, приводит к тому, что
импульс релятивистской частицы будет
определяться выражением
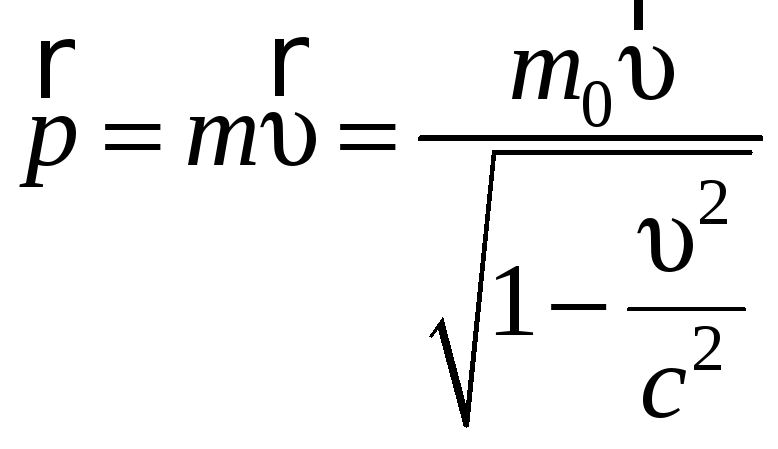 ,
(7.6.1)
,
(7.6.1)
где
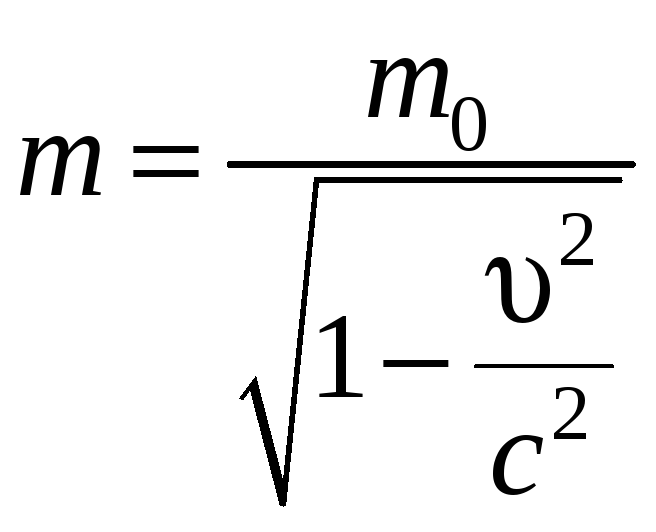 − релятивистская
масса
движущейся частицы; m0
− массой
покоя частицы,
т. е.
масса частицы в собственной системе
отсчета.
− релятивистская
масса
движущейся частицы; m0
− массой
покоя частицы,
т. е.
масса частицы в собственной системе
отсчета.
Выражение (7.6.1) позволяет сделать важнейший вывод: в релятивистской динамике масса частицы зависит от скорости ее движения. При << c (это соотношение всегда выполняется в классической механике), получаем m = m0 = const.
7.7. Релятивистские законы Ньютона
Первый закон Ньютона, являющийся выражением принципа относительности, сохраняет свою классическую формулировку в релятивистской динамике.
Выражение для второго закона Ньютона в релятивистской механике также сохраняет свою классическую формулировку при условии, что импульс определяется по формуле (7.6.1)
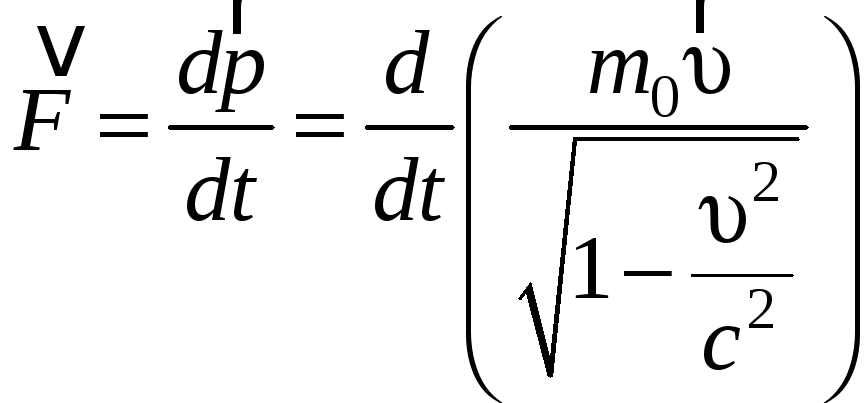 .
(7.7.1)
.
(7.7.1)
Релятивистское уравнение (7.7.1) инвариантно относительно преобразований Лоренца.
Третий закон Ньютона в релятивистской динамике справедлив только для контактных сил. В классической механике для сил, действующих на расстоянии, предполагается мгновенная передача взаимодействия без материального посредника. Это несовместимо с релятивистским положением о том, что максимальная скорость передачи взаимодействия не может быть больше скорости света в вакууме. Поэтому для взаимодействий с конечной скоростью распространения третий закон Ньютона в своей классической формулировке неприменим.
7.8. Энергия релятивистской частицы. Закон взаимосвязи массы и энергии
Понятие энергии в релятивистской механике сохраняет тот же смысл, что и в классической механике. Однако требование инвариантности уравнений релятивистской механики относительно преобразований Лоренца приводит к установлению взаимосвязи между энергией E и массой т частицы, а также к изменению выражения для ее кинетической энергии К.
Найдем
выражение для кинетической энергии
материальной точки в релятивистской
механике. Изменение кинетической энергии
материальной точки при элементарном
перемещении
![]() равно
работе, совершаемой силой
равно
работе, совершаемой силой
![]() ,
действующей на точку, при этом перемещении
,
действующей на точку, при этом перемещении
![]() .
(7.8.1)
.
(7.8.1)
Воспользуемся
релятивистским выражением второго
закона Ньютона (7.7.1),
и с учетом
![]() получаем
получаем
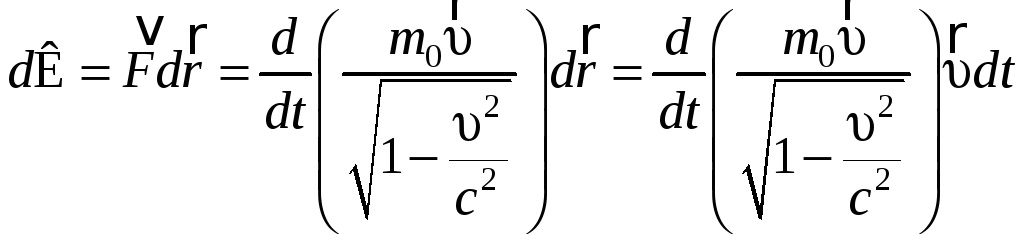
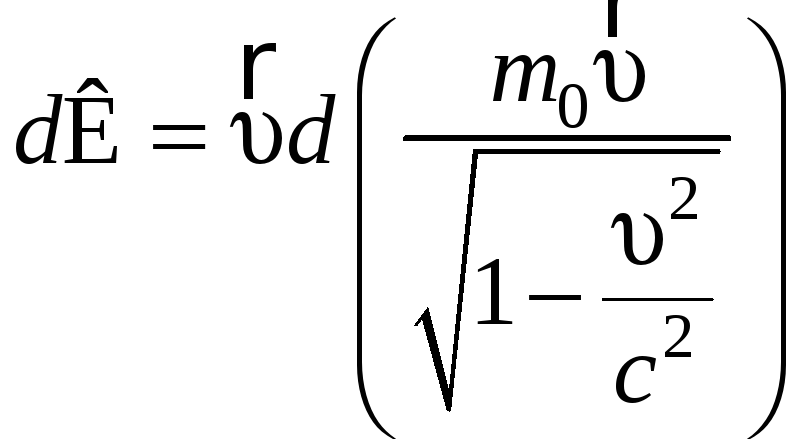 .
(7.8.2)
.
(7.8.2)
С учетом
 из выражения (7.8.2) получаем
из выражения (7.8.2) получаем
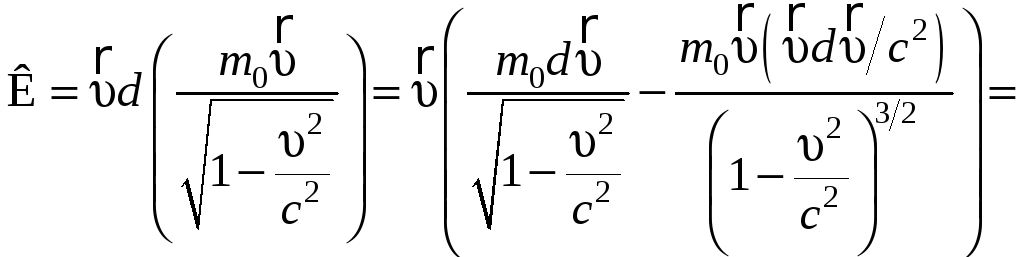

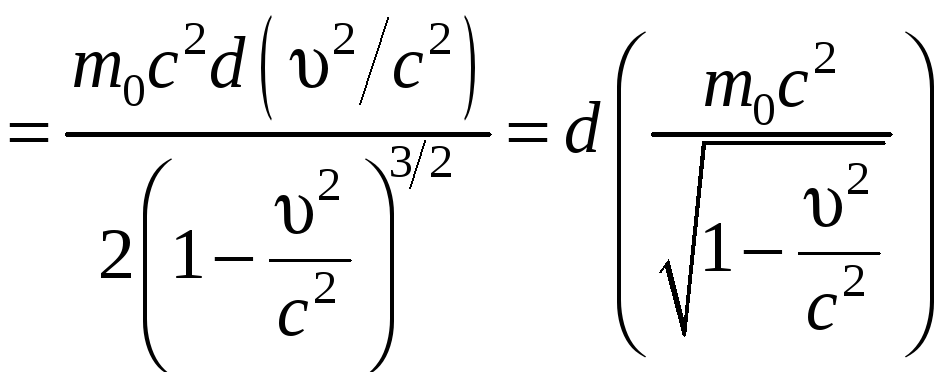
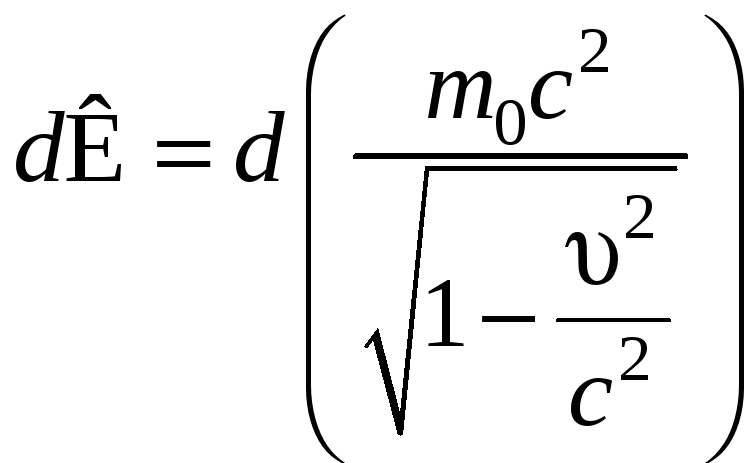 .
(7.8.3)
.
(7.8.3)
Интегрирование уравнения (7.8.3) приводит к выражению
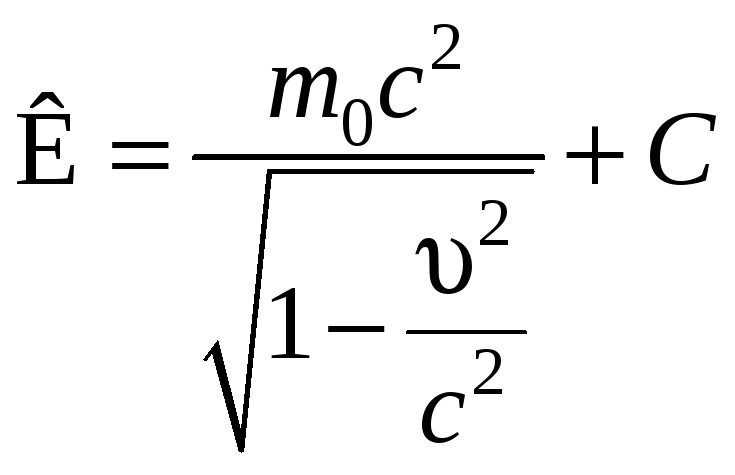 ,
(7.8.4)
,
(7.8.4)
где С – постоянная интегрирования.
Найдем постоянную интегрирования С. Для этого воспользуемся условием, что при = 0 кинетическая энергия К должна быть тоже равна нулю. С учетом этого из выражения (7.8.4) получаем C = −m0 c2. Таким образом, релятивистское выражение для кинетической энергии имеет вид
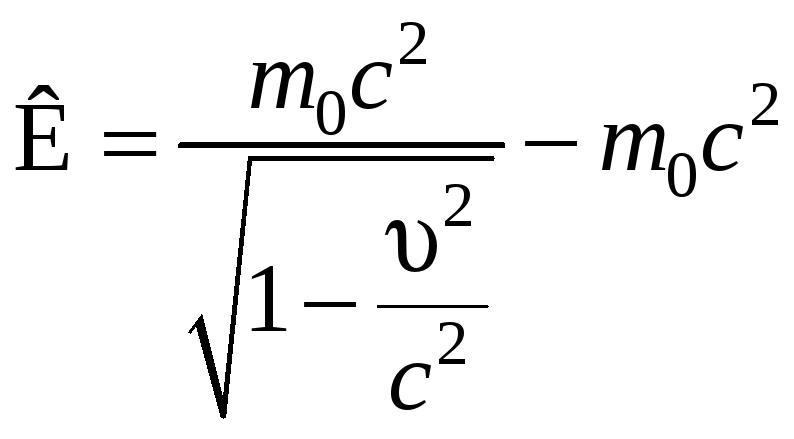 .
(7.8.5)
.
(7.8.5)
Величина
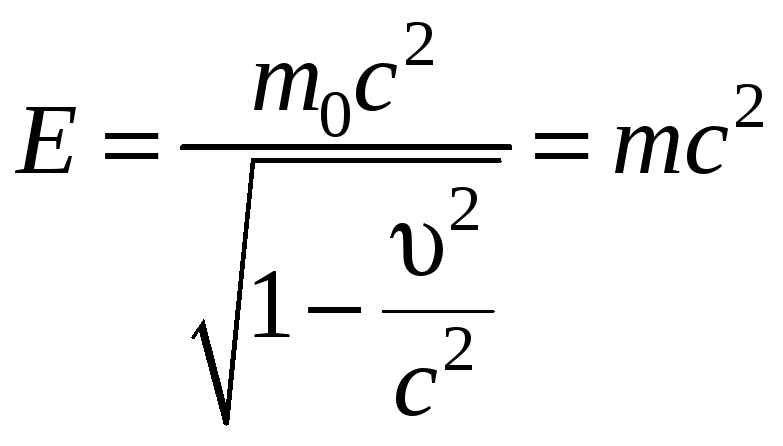 (7.8.6)
(7.8.6)
называется полной энергией свободной частицы (при отсутствии внешних полей).
Величина
E0 = m0 c2 (7.8.7)
называется энергией покоя (при = 0).
С учетом формул (7.8.6, 7.8.7) выражение для кинетической энергии (7.8.5) можно записать в виде
К = E − E0 = mc2 − m0 c2. (7.8.8)
При
<< c,
с учетом
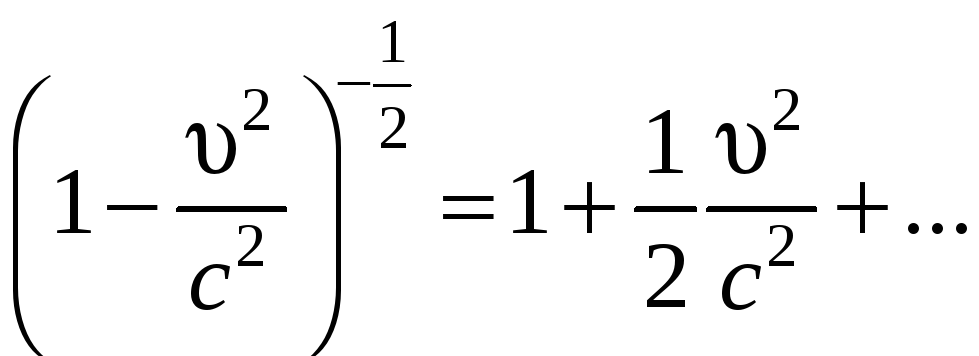 ,
получаем выражение для кинетической
энергии в классической механике
,
получаем выражение для кинетической
энергии в классической механике
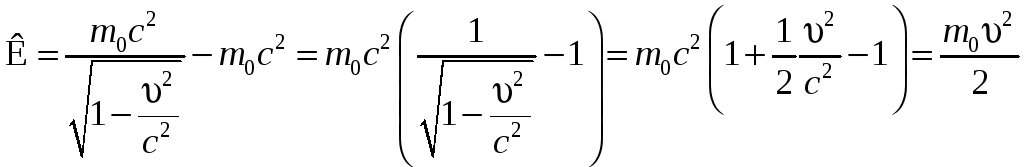 .
(7.8.9)
.
(7.8.9)
Таким образом, при малых скоростях движения материальной точки ее кинетическая энергия, вычисленная по релятивистской формуле (7.8.5), совпадает с выражением (7.8.9) для энергии в классической механике.
Из соотношения (7.8.6) следует также важный вывод: энергия тела пропорциональна его релятивистской массе. Всякое изменение энергии тела сопровождается изменением его релятивистской массы и, наоборот, всякое изменение релятивистской массы сопровождается изменением энергии тела
E = mc2. (7.8.10)
Это утверждение носит название закона взаимосвязи релятивистской массы и энергии.
