Московский Энергетический Институт

(технический университет)

Кафедра ОФ и ЯС

Лаборатория электричества и магнетизма.

Лабораторная работа №45

Наблюдение явления интерференции: измерение радиуса кривизны линзы с помощью колец ньютона

Группа:
Студент:
Преподаватель:
К работе допущен:
Дата выполнения:
Работу сделал:
Работу сдал:

МОСКВА 2005

Цель работы - наблюдение интерференции в экспериментальной уста­новке «кольца Ньютона», определение радиуса кривизны линзы, приобретение навыков работы с серийно выпускаемым микроскопом «Биолам-Р».

1. Теоретические основы работы

Волновые свойства света наиболее отчетливо проявляются в явлении ин­терференции света. Для наблюдения интерференции необходимо свет от одно­го источника разделить на два пучка и затем свести их воедино. Если разность хода этих пучков не превышает длины одного цуга, то все изменения фаз в пучках происходят согласованно. Такие пучки называются когерентными.

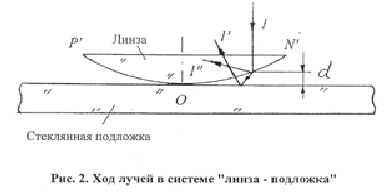
Один из методов получения когерентных пучков реализуется в экспери­ментальной установке «кольца Ньютона». В этой установке разделение пучка монохроматического света на два когерентных происходит при их отражении от сферической поверхности плоско-выпуклой линзы и от верхней грани плос­копараллельной стеклянной пластины (рис.1). Ход лучей показан на рис.2. Здесь на линзу падает почти параллельный пучок света (луч 1) нормально к плоскости линзы и стеклянной пластины (подложке); луч 1’ формируется в ре­зультате отражения от сферической поверхности линзы P’ON; луч 1” - от верх­ней поверхности стеклянной пластины PON (подложки). При этом геометриче­скую разность хода δ между лучами 1’ и 1” с достаточной степенью точности можно принять равной 2d (так как их встреча произойдет вблизи поверхности Р’ON’ - рис.2), где d - величина зазора между сферической поверхностью линзы и верхней поверхностью подложки в точке М'. Точка М' - точка падения данно­го луча (рис.1). Из треугольника СО'М' (точка С - геометрический центр сфе­рической поверхности линзы) находим

,(1)

Здесь R - радиус сферической поверхности линзы, r = О'М'. С учетом условия, что d « R можно записать r² = 2Rd или 2d = r²/R.

Оптическая разность хода Δ равна разности оптических длин пути лучей 1’ и 1”:

, где n₂ = п- показатель преломления среды, находящейся в зазоре между линзой и подложкой (воздуха), n₁ - показатель преломления ма­териала линзы (стекла); l₂ - геометрическая длина пути луча l"; l₁ - геометриче­ская длина пути луча l’. Так как , а (лучи встречаются вблизи поверхности ON' см. рис.1 и 2), то

, (2)

где λ – длина волны света.

Слагаемое λ/2 в последнем уравнении является эквивалентом прохожде­нию волной добавочного пути. Добавочный путь возникает из-за изменения фазы светового вектора Е волны на π при ее отражении от оптически более плотной среды — подложки в точке М. Так как в настоящей установке средой между линзой и подложкой является воздух, то .

Из осевой симметрии колец Ньютона следует, что линии постоянной раз­ности хода будут представлять собой систему концентрических колец. Каждо­му кольцу соответствует постоянная толщина зазора d между линзой и под­ложкой, поэтому кольца Ньютона называют полосами равной толщины. Радиусы темных колец определяются условиями интерференционных минимумов Δ = (2т + 1)λ/2 , радиусы светлых - условиями интерференционных максимумов Δ = 2т λ /2 . Отсюда с учетом (2) при п = 1 для радиусов темных колец получим

, (3)

а для радиусов светлых колец

. (4)

Здесь m = 1, 2, 3 ... - номер кольца. Определив радиусы темных колец для известной длины волны λ, монохроматического света, рассчитаем радиус кривизны линзы

, (5)

Кроме описанной выше схемы наблюдения интерференционной картины в отраженном свете, возможно наблюдение колец Ньютона в проходящем све­те. В отраженном свете интерферируют пучки примерно одинаковой интенсив­ности, в прошедшем - существенно отличающиеся по интенсивности. Поэтому в последнем случае интерференционная картина будет значительно менее от­четливой.