2.2. Расчет распределения интенсивности света на экране

при дифракции на одной щели

В приведённом ниже расчёте по-прежнему пользуемся принципом Гюйгенса-Френеля. Рассмотрим плоскую монохроматическую волну, падающую на узкую прямоугольную щель. Пусть уравнение волны даётся соотношением:

, (3)

где – амплитуда волны,– волновое число,– расстояние, которое волна прошла от фронтаAB. Вклад элементарного участка волновой поверхности шириной , отстоящего на расстояниих от точки А (см. рис. 1) даётся соотношением:

. (4)

Разность фаз между волнами от различных участков щели создаётся в процессе образования нового фронта AC (напоминаем, что линза не создаёт дополнительной разности хода). Волна, создаваемая элементарным участком, расположенным на расстоянии от края щели, может быть представлена в виде:

.(5)

Проинтегрировав это выражение по всей ширине щели b, найдем амплитуду результирующей волны в соответствующей точке экрана М_φ. Запишем выражение для амплитуды волны E_0 в точке М_φ:

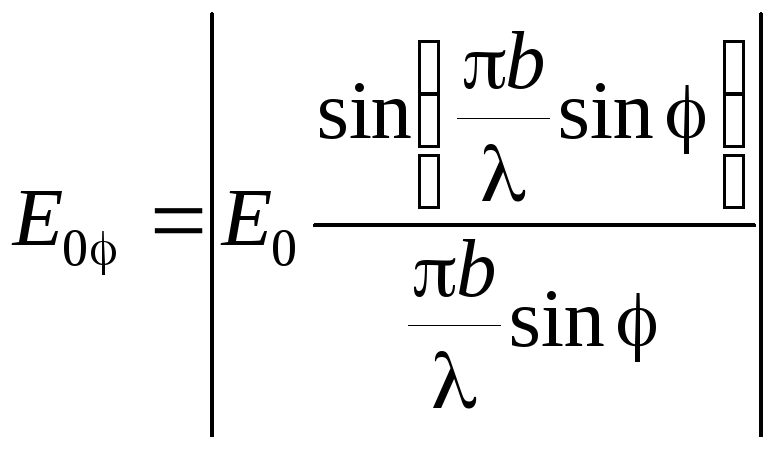. (6)

Вводя обозначение

,(7)

получим

.(8)

При u  0 sin u  u, lim(sin u/u) = 1, поэтому при  = 0 дробь в выражении (6) превращается в единицу. Отсюда следует, что E₀ есть амплитуда в точке М₀ (против центра линзы).

Интенсивность света пропорциональна квадрату амплитуды. Следовательно,

. (9)

Из формул (6,9) следует, что если

bsin =  k (k = 1,2,3, …),

то интенсивность обращается в нуль (наблюдаются минимумы порядков

k =1, k = 2, и т.д.) Это согласуется с формулой (1).

График функции представлен на рис. 3.

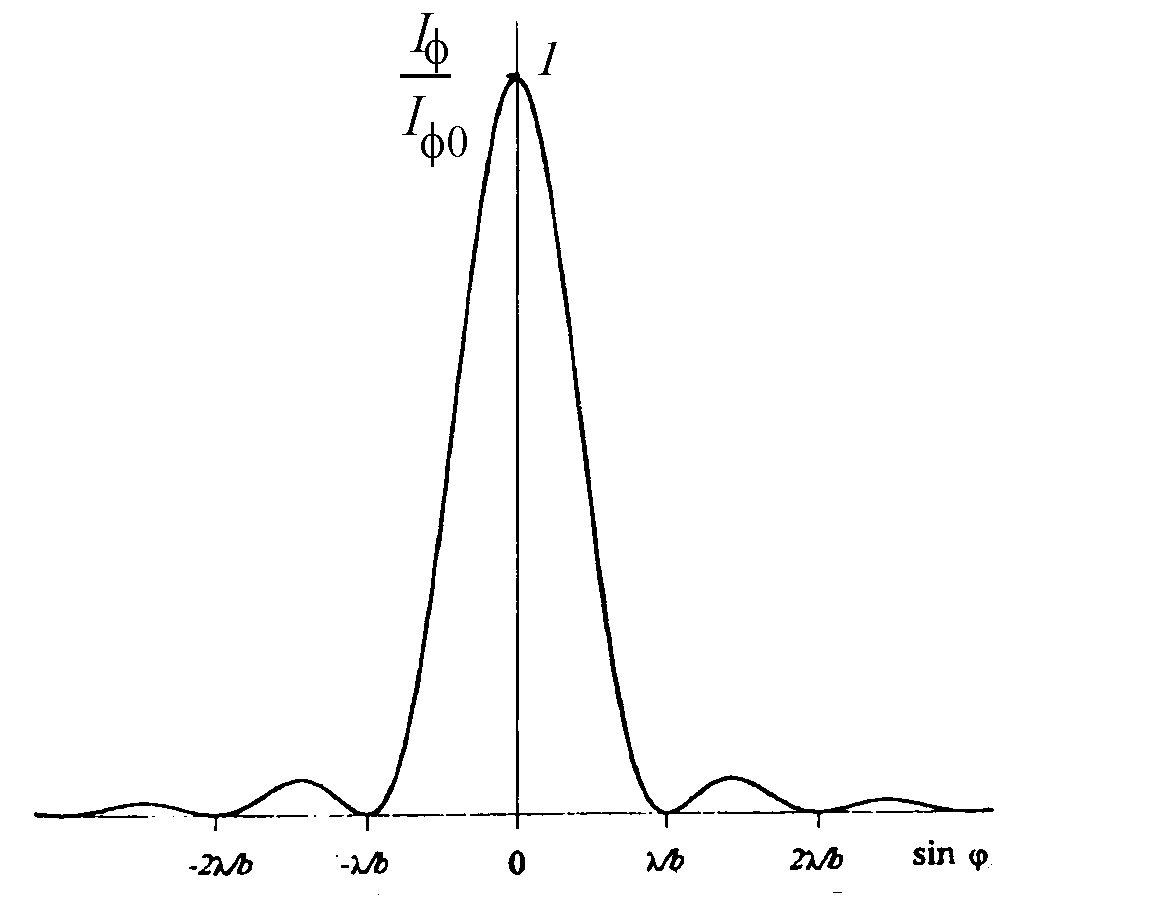
Рис. 3. График функции для одной щели (зависимость интенсивности света от угла дифракции  дана в относительных единицах)

2.3. Дифракция на двух щелях

Для простейшего анализа дифракционной картины при дифракции на двух параллельных щелях воспользуемся методом зон Френеля. Пусть плоская волна падает на экран Э₁ с двумя одинаковыми щелями шириной b (см. рис 4а). Здесь также показаны собирающая линза Л и экран Э₂. При падении плоской волны нормально к экрану Э₁ каждая щель создаёт дифракционную картину, описанную в п. 2.1. Но, кроме этого, будет происходить интерференция пучков света от разных щелей. В результате произойдёт существенное перераспределение света на экране Э₂.

Рис. 4 (а). Оптическая схема опыта по наблюдению дифракции света от двух щелей

Ограничимся простейшими рассуждениями. Разность хода между лучами, идущими от точек из середины щелей, расстояние между которыми равно d, а также от любых двух "соответствующих" точек соседних щелей (разделенных расстоянием d) равна . Поэтому при условии

; (11)

свет от обеих щелей приходит в точку М_φ в одной фазе. Условия (11) называют условиями "главных максимумов" по аналогии с дифракционной картиной на дифракционной решетке, так как случай двух щелей – частный случай дифракции на дифракционной решётке с N щелями. Условие

; (12)

означает, что волны от соседних щелей будут взаимно ослаблять друг друга. Мы получаем условия дополнительных (побочных) минимумов дифракционной картины (напомним о существовании минимумов дифракционной картины (1) при дифракции от одной щели).

При значении обе щели будут создавать волны в одной фазе; результирующая амплитуда

; .(13)

Интенсивность центрального максимума увеличилась в четыре раза (по сравнению с центральным максимумом, полученным от одной щели).

Результирующее колебание в точке М_φ на экране Э₂ представляет собой сумму N колебаний (в случае двух щелей N = 2) с одинаковой амплитудой E_φ, сдвинутых друг относительно друга по фазе на одну и ту же величину d (рис. 4а). Интенсивность при этих условиях равна:

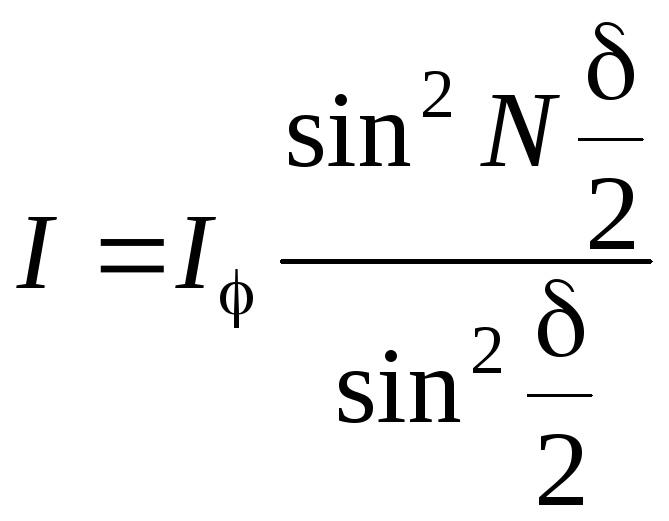, (14)

где разность фаз d определяется соотношением:

(15)

Подставив в формулу (14) соотношение (10), с учетом (15) имеем:

(16)

График функции I_φ, определяемый выражением (16), представлен на рис.4б. Здесь кривая 1 соответствует условиям: ,N = 2 (две щели); кривая 2 – условиям ;(четыре щели); пунктирная линия показывает интенсивность, создаваемую одной щелью. Кривые 1 и 2 нормированы на интенсивностьI₀.

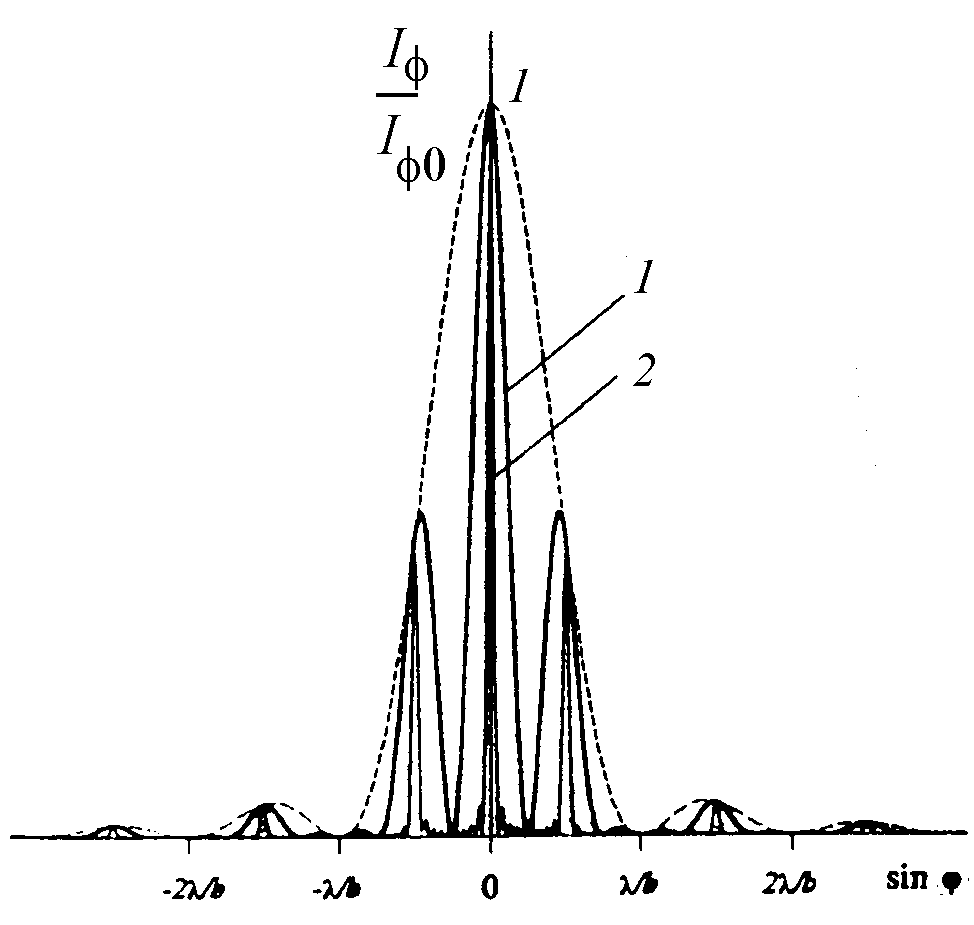
Рис. 4 (б). График функции I_φ, определяемый выражением (16), (в относительных единицах)