
- •Предел функции
- •Предел функции в точке
- •Бесконечные пределы функций
- •Пределы функций на бесконечности
- •Свойства функций, имеющих пределы
- •Замечательные пределы
- •Односторонние пределы
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •Бесконечно малые величины
- •Основные эквивалентности при
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
Замечательные пределы
Рассмотрим несколько пределов, которые носят такое название, поскольку они широко используются при решении как теоретических, так и практических задач.
а) Первый замечательный предел:
![]() .
.
б) Второй замечательный предел:
 ,
,
здесь
символом «![]() »
обозначено иррациональное число
»
обозначено иррациональное число
![]()
Равенство
![]() также называют вторым замечательным
пределом.
также называют вторым замечательным
пределом.
Рассмотрим пример
Я. И. Перельмана,
дающий интерпретацию числа
![]() в задаче о сложных процентах. Число
в задаче о сложных процентах. Число
![]() есть предел
есть предел
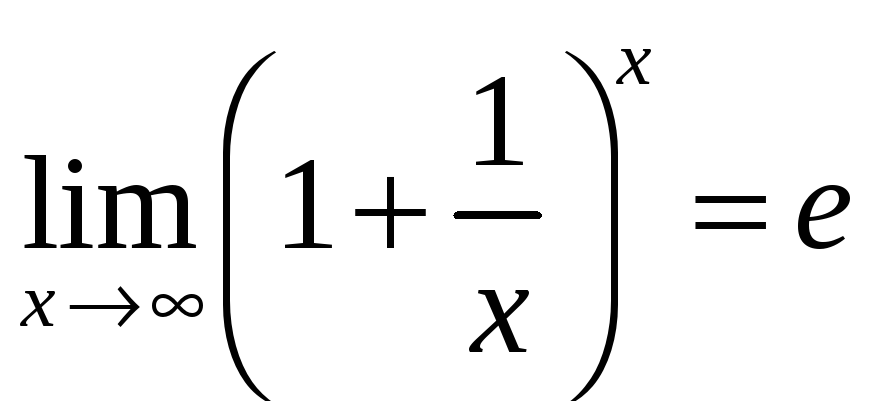 .
В сбербанках процентные деньги
присоединяются к основному капиталу
ежегодно. Если присоединение совершается
чаще, то капитал растет быстрее, так как
в образовании процентов участвует
большая сумма. Возьмем чисто теоретический,
весьма упрощенный пример. Пусть в банк
положено 100 ден. ед. из расчета 100 % годовых.
Если процентные деньги будут присоединены
к основному капиталу лишь по истечении
года, то к этому сроку 100 ден. ед. превратятся
в 200 ден.ед. Посмотрим теперь, во что
превратятся 100 ден. ед., если процентные
деньги присоединять к основному капиталу
каждые полгода. По истечении полугодия
100 ден. ед. вырастут в
.
В сбербанках процентные деньги
присоединяются к основному капиталу
ежегодно. Если присоединение совершается
чаще, то капитал растет быстрее, так как
в образовании процентов участвует
большая сумма. Возьмем чисто теоретический,
весьма упрощенный пример. Пусть в банк
положено 100 ден. ед. из расчета 100 % годовых.
Если процентные деньги будут присоединены
к основному капиталу лишь по истечении
года, то к этому сроку 100 ден. ед. превратятся
в 200 ден.ед. Посмотрим теперь, во что
превратятся 100 ден. ед., если процентные
деньги присоединять к основному капиталу
каждые полгода. По истечении полугодия
100 ден. ед. вырастут в
![]() ,
а еще через полгода – в
,
а еще через полгода – в
![]() (ден. ед.). Если присоединение делать
каждые
(ден. ед.). Если присоединение делать
каждые
![]() года, то по истечении года 100 ден. ед.
превратятся в
года, то по истечении года 100 ден. ед.
превратятся в
![]() (ден. ед.). Будем учащать сроки присоединения
процентных денег до 0,1 года, до 0,01 года,
до 0,001 года и т.д. Тогда из 100 ден. ед.
спустя год получится:
(ден. ед.). Будем учащать сроки присоединения
процентных денег до 0,1 года, до 0,01 года,
до 0,001 года и т.д. Тогда из 100 ден. ед.
спустя год получится:
![]() (ден. ед.),
(ден. ед.),
![]() (ден. ед.),
(ден. ед.),
![]() (ден. ед.).
(ден. ед.).
При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что
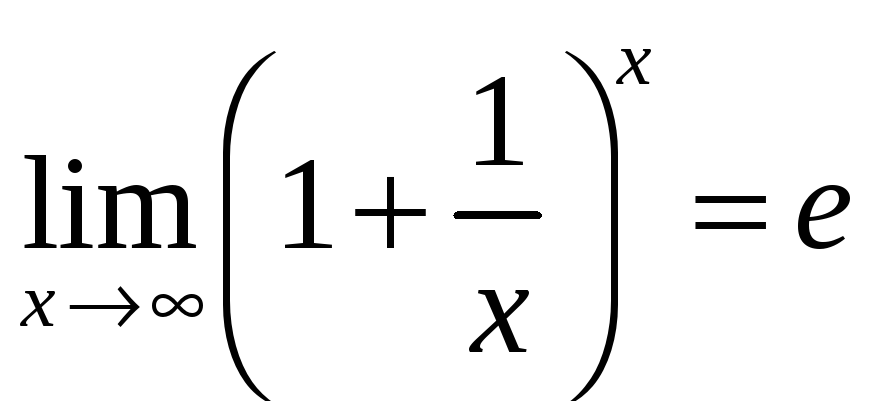 .
.
К замечательным пределам относят равенства
![]() ,
в частности,
,
в частности,
![]() ,
,
![]() ,
в частности,
,
в частности,
![]() ,
,
![]() .
.
-
Односторонние пределы
Понятие предела
функции в точке можно разложить на две
составляющие части: предел функции
![]() ,
когда
,
когда
![]() ,
оставаясь меньше
,
оставаясь меньше
![]() ,
т.е.
,
т.е.
![]() слева, и предел функции
слева, и предел функции
![]() ,
когда
,
когда
![]() ,
оставаясь больше
,
оставаясь больше
![]() ,
т.е.
,
т.е.
![]() справа. В этом случае говорят об
односторонних пределах, обозначая их
справа. В этом случае говорят об
односторонних пределах, обозначая их
![]() или
или
![]() (для левостороннего предела) и
(для левостороннего предела) и
![]() или
или
![]() (для правостороннего предела).
(для правостороннего предела).
Определение.
Пусть точка
![]() является предельной точкой для множества
является предельной точкой для множества
![]() .
Тогда число
.
Тогда число
![]() называется пределом слева функции
называется пределом слева функции
![]() при
при
![]() ,
если
,
если
![]() .
.
Определение.
Пусть точка
![]() является предельной точкой для множества
является предельной точкой для множества
![]() .
Тогда число
.
Тогда число
![]() называется пределом справа функции
называется пределом справа функции
![]() при
при
![]() ,
если
,
если
![]() .
.
Сравнение этих
определений и определения предела
функции в точке
![]() показывает, что если функция имеет
предел в точке
показывает, что если функция имеет
предел в точке
![]() ,
то этот предел одновременно является
ее левосторонним и правосторонним
пределами в этой точке.
,
то этот предел одновременно является
ее левосторонним и правосторонним
пределами в этой точке.
Связь между пределом и односторонними пределами функции устанавливает следующая теорема.
Теорема. Для
того чтобы существовал
![]() необходимо и достаточно, чтобы существовали
односторонние пределы
необходимо и достаточно, чтобы существовали
односторонние пределы
![]() и
и
![]() ,
и
,
и
![]() =
=![]() .
В этом случае общее значение односторонних
пределов равно значению предела функции:
.
В этом случае общее значение односторонних
пределов равно значению предела функции:
![]() .
.
Замечание. Предел
элементарной функции
![]() при
при
![]() ,
где
,
где
![]() принадлежит области её определения,
равен значению функции при
принадлежит области её определения,
равен значению функции при
![]() .
В этом случае говорят, что функция
.
В этом случае говорят, что функция
![]() непрерывна в точке
непрерывна в точке
![]() .
.
