4.3. Теорема котельникова.

Теорема Котельникова называется также теоремой отсчетов или теоремой о выборках. Выборкой называется отсчет амплитуды сигнала в определенный момент времени. Термин "выборка" взят от английского слова samples.

Теорема Котельникова определяет минимальную частоту взятия отсчетов при равномерной дискретизации сигнала с ограниченным спектром, т.е. величину, обратную максимальному временному шагу дискретизации (интервалу Найквиста): 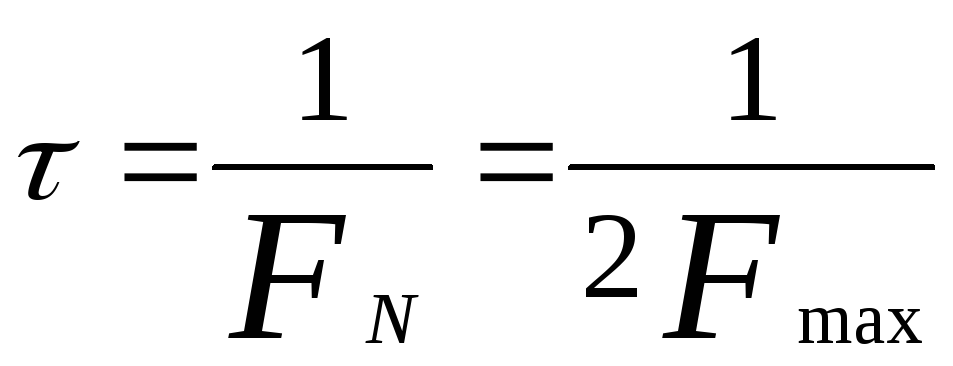. Минимальная частота отсчетов значений в секунду должна быть вдвое больше самой высокой частоты спектра, т.е.

Сигнал, не содержащий в своем спектре частот выше F_m, полностью определяется 2F_m независимыми значениями в секунду.

Эта теорема позволяет на интервале длительности передачи сообщения t_s заменить непрерывный сигнал с ограниченным спектром равномерной последовательностью его дискретных значений, причем их нужно не бесконечное число, а вполне определенное, равное 2F_m.t_s

Другая формулировка теоремы Котельникова:

Любая непрерывная функция , спектр которой ограничен максимальной частотой , полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал Найквиста:

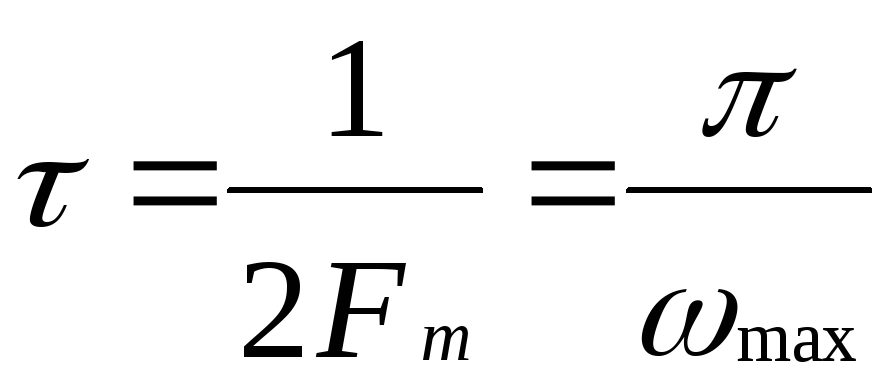
4.4.Информационная емкость дискретного сигнала (сообщения). Формула шеннона.

Уровень шумов (помех) не позволяет точно определить амплитуду сигнала и в этом смысле вносит некоторую неопределенность в значение отсчетов сигнала. Если бы шума не существовало, то число дискретных уровней сигнала было бы бесконечным. Величина шума определяет степени различимости отдельных уровней амплитуды сигнала. Максимально возможное число уровней (состояний) N сигнала в одной выборке из-за наличия шума равно

N=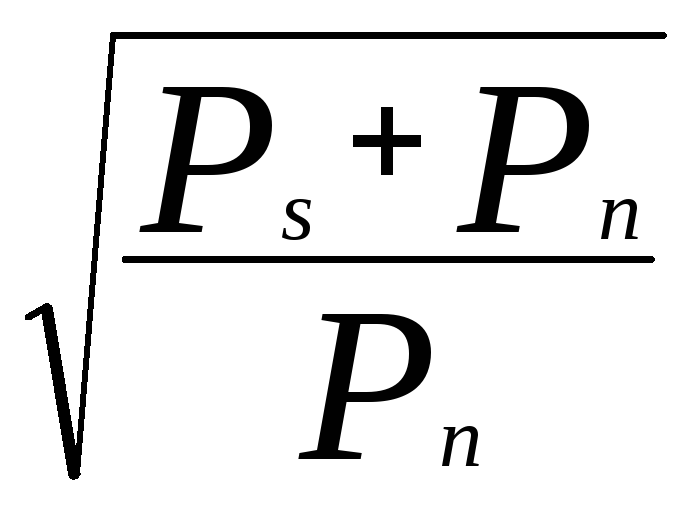, где

- средняя мощность сигнала;

- средняя мощность шума;

Если число уровней (состояний) системы в одной выборке (на один отсчет) равно N, то это равносильно информации, даваемой i битами (Формула Хартли).

N=2ⁱ; log₂N=ilog₂2; log₂N=i; i=log₂N; i=log₂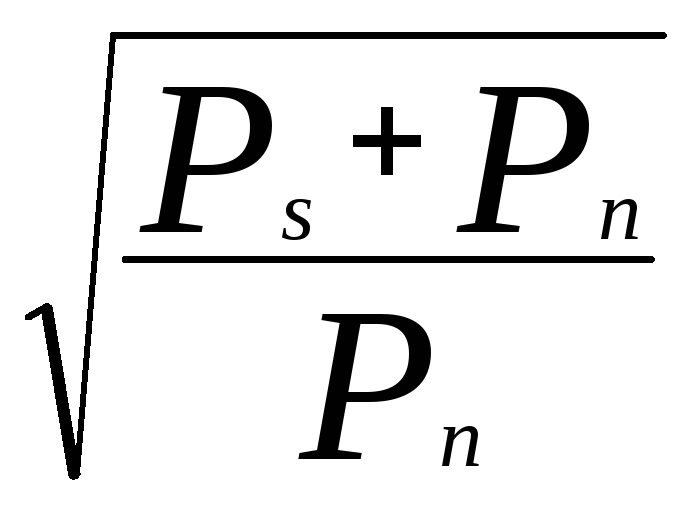

Из теоремы Котельникова следует, что на интервале длительности передачи сообщения t_s непрерывный сигнал с ограниченным спектром можно заменить последовательностью из 2F_m.t_s его дискретных значений. Поэтому информационная емкость дискретного сигнала (сообщения) за время передачи состав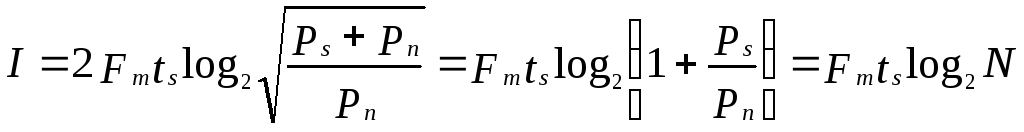ит

(бит)

- длительность передачи сообщения;

- максимальная частота из передаваемого спектра частот;

- частота выборок по Котельникову;

- количество выборок по Котельникову за время передачи сообщения;

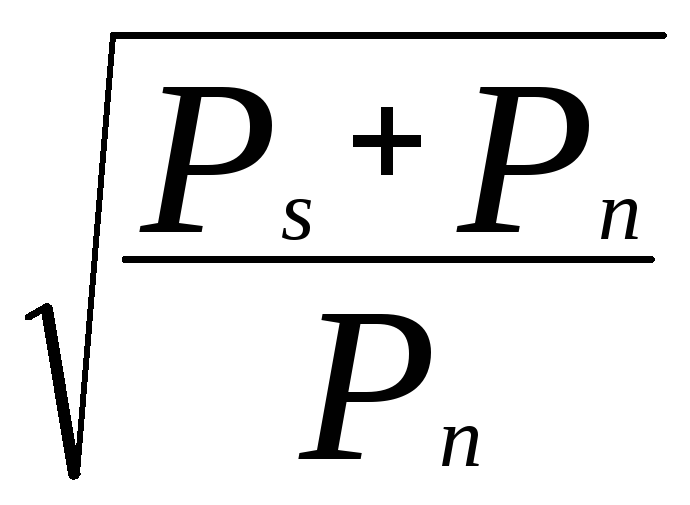- максимально возможное число уровней N сигнала в одной выборке из-за наличия шума;

- средняя мощность сигнала равна квадрату амплитуды сигнала;

- средняя мощность шума равна квадрату амплитуды шума.

Информационные возможности сигнала возрастают с расширением спектра его частот и превышением уровня сигнала над уровнем помех.

4.5. Предельная скорость передачи информации по шеннону. Формула хартли - шеннона.

Предельная скорость передачи информации относится к фундаментальным понятиям теории связи. Она служит одной из главных характеристик канала передачи информации.

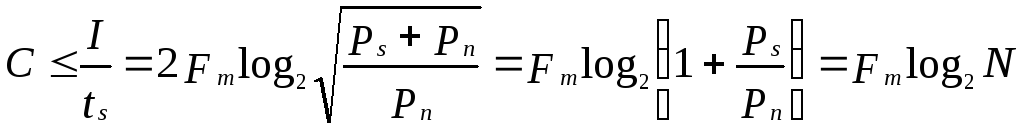(бит/с)

Основными факторами, ограничивающими скорость передачи информации, являются полоса частот F_m и уровень помех P_n. Полоса частот F_m и мощность сигнала P_s входят в формулу таким образом, что для C=Const при сужении полосы F_m необходимо увеличивать мощность сигнала P_s и наоборот.

Оценка скорости передачи информации и предельных возможностей канала связи представляет большой практический и теоретический интерес. Выявление принципиальных ограничений в передаче информации является интересной физической и математической задачей.