6.2. Измерение отношения сигнал – шум.

Отношение наибольшей мгновенной мощности сигнала P_max к наименьшей P_min (динамический диапазон сигнала D_s) обычно измеряется в децибелах.

Бел – это такая разность уровней мощности, отношение которых равно 10 и соответственно десятичный логарифм этого отношения равен 1.

Децибел – это десятичная часть Бела.

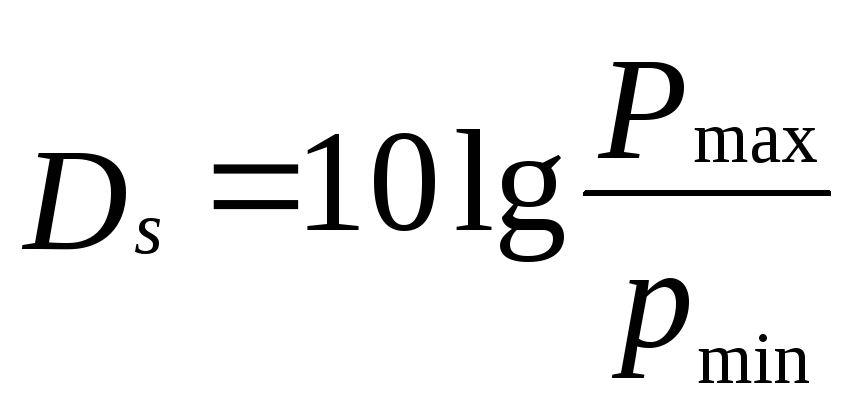(дБ) разница уровней в децибелах есть десять десятичных логарифмов отношения мощностей.

Т.к. =- средняя мощность сигнала равна квадрату амплитуды сигнала и т.к. = - средняя мощность шума равна квадрату амплитуды шума, то

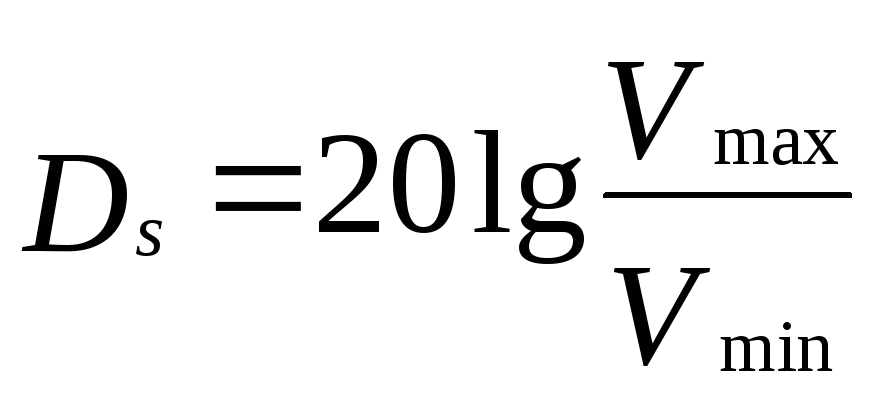(дБ) разница уровней в децибелах есть двадцать десятичных логарифмов отношения напряжений.

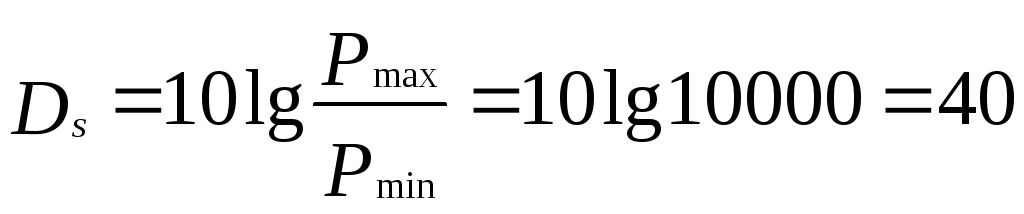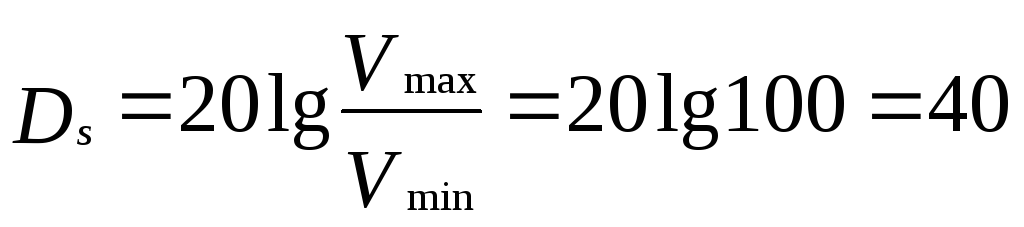Для хорошего качества речи, передаваемой по телефону, необходимо обеспечить отношение сигнал-шум по мощности примерно 10000, или 40 децибел (дБ): (дБ). Другими словами, необходимо обеспечить отношение сигнал-шум по напряжению примерно 100: (дБ)

Опытные радисты могут разобрать речь при отношении сигнал - шум по напряжению около десяти, но при условии, что передаваемый текст знаком и привычен.

6.3. Дискретизация и кодирование аналогового сигнала.

Непрерывное сообщение может быть представлено непрерывной функцией, заданной на некотором отрезке [а, Ь]. Непрерывное сообщение можно преобразовать в дискретное (такая процедура называется дискретизацией).

Для этого из бесконечного множества значений этой функции (параметра сигнала) выбирается их определенное число, которое приближенно может характеризовать остальные значения. Один из способов такого выбора состоит в следующем. Область определения функции разбивается точками на отрезки равной длины x₁, x₂…, x_n и на каждом из этих отрезков значение функции принимается постоянным и равным, например, среднему значению на этом отрезке; полученная на этом этапе функция называется в математике ступенчатой.

Следующий шаг - проецирование значений «ступенек» на ось значений функции y₁, y₂…, y_n является дискретным представлением непрерывной функции, точность которого можно неограниченно улучшать путем уменьшения длин отрезков при разбиении области значений аргумента.

ПРОЦЕДУРА ДИСКРЕТИЗАЦИИ НЕПРЕРЫВНОГО СООБЩЕНИЯ.

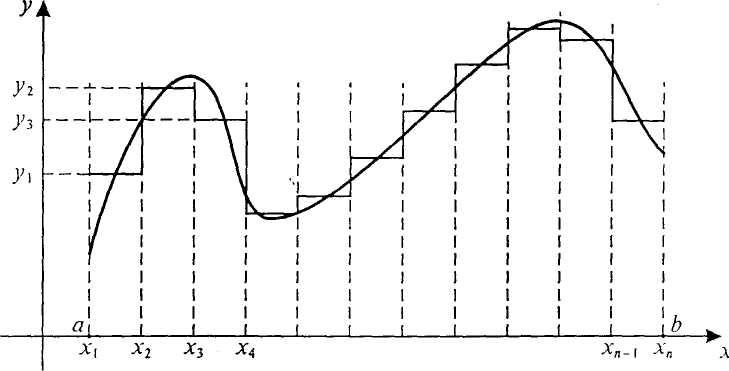
Ось значений функции можно разбить на отрезки с заданным шагом и отобразить каждый из выделенных отрезков из области определения функции в соответствующий отрезок из множества значений. В итоге получим конечное множество чисел, определяемых, например, по середине или одной из границ таких отрезков.

Таким образом, любое сообщение может быть представлено как дискретное, т.е. последовательностью знаков некоторого алфавита.

Ввиду преимущества двоичных сигналов перед аналоговыми сигналами в настоящее время широко используются двоичные каналы для передачи аналоговых речевых сигналов. Внедрение подобных систем на междугородных линиях связи значительно улучшило качество связи.

Для дискретизации аналогового речевого сигнала необходимо:

• преобразовать аналоговый речевой сигнал в цифровой код;

• передать цифровой сигнал по линии связи, регенерируя его на каждом из промежуточных усилительных пунктов (при этом устраняются помехи).

• перед подачей в телефонную трубку цифровой сигнал снова превратить в аналоговый.

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер - цифровая машина, т.е. внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки.

Существуют и другие вычислительные машины - аналоговые ЭВМ. Они используются обычно для решения задач специального характера и широкой публике практически не известны. Эти ЭВМ в принципе не нуждаются в дискретизации входной информации, так как ее внутреннее представление у них непрерывно. В этом случае все наоборот - если внешняя информация дискретна, то ее «перед употреблением» необходимо преобразовать в непрерывную.

Превратить в дискретный двоичный можно не только речевой, но и любой другой аналоговый сигнал. В качестве примера попробуем сконструировать простейший датчик углового положения фюзеляжа.

Возьмем отвес - жесткий стержень с грузом на конце, закрепленный на горизонтальной оси 0. Верхний конец стержня соединим с подвижным контактом потенциометра, а к крайним выводам потенциометра подключим источники напряжения -10 В и + 10 В. Если фюзеляж самолета находится в горизонтальном положении, подвижный контакт будет в середине резистивной подковки потенциометра, а потенциал на нем U обратится в нуль. Стоит самолету наклониться вперед, допустим, войти в пике, движок потенциометра переместится влево по подковке и потенциал U станет отрицательным. Если же носовая часть самолета будет направлена вверх, потенциал V станет положительным. Пусть при наклоне фюзеляжа на угол ± 20° потенциал U изменяется от + 10 до - 10 В. Крутизна характеристики преобразования угол - напряжение для такого датчика составит 0,5 В на градус. Таким образом, мы получим аналоговый сигнал углового положения самолета.

ДИСКРЕТИЗАЦИЯ ПО УРОВНЮ АНАЛОГОВОГО СИГНАЛА.

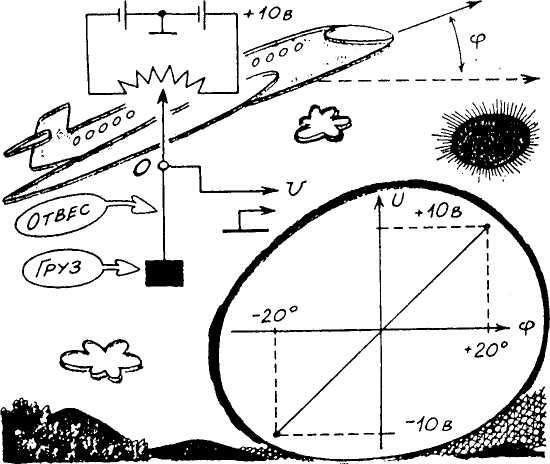
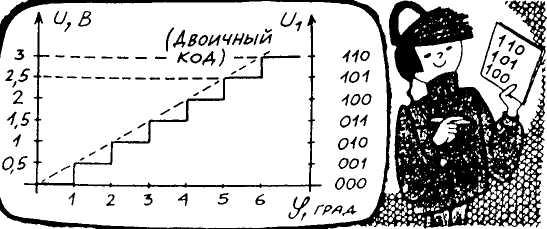
Для преобразования этого сигнала в цифровую форму необходимо задаться шагом дискретизации - минимальным изменением напряжения, соответствующим изменению цифрового кода на единицу. Если в нашем простейшем случае достаточна точность 1°, то шаг дискретизации будет равен 0,5 В. Число шагов дискретизации, на которое изменилось напряжение U, и будет являться углом наклона фюзеляжа, выраженным в градусах. Его значение можно представить и двоичным кодом, как это показано на рисунке.

Для преобразования аналоговых величин в цифровой код служат специальные электронные устройства – аналого-цифровые преобразователи (АЦП). Полученный цифровой код углового положения фюзеляжа поступает в цифровой процессор, выполняющий функции и сравнивающего устройства, и системы регулирования. Сюда же поступают сведения и о положении самолета в других плоскостях пространства, и о положении рулей. Процессор вырабатывает сигнал, управляющий рулями. При цифровой обработке информации можно получить большую точность регулирования и управления. Этим и объясняется широкое применение цифровой техники в системах управления.

С какой точностью, например, можно измерить напряжение с помощью обычного стрелочного прибора? Лучшие лабораторные магнитоэлектрические приборы с зеркальной шкалой обеспечивают точность отсчета не более 0,2%, что составляет 2^-3 В то же время цифровые вольтметры могут иметь пять-шесть разрядов, что обеспечивает точность измерений на два-три порядка (в 100... I000 раз) выше.