
- •Динамика машинного агрегата
- •Структурный анализ рычажного механизма
- •Определение размеров и параметров рычажного механизма
- •3.3. Определение кинематических характеристик механизма.
- •3.3.1. Графическая кинематика механизма.
- •3.3.1.1. Построение планов положений.
- •3.3.2. Аналитическая кинематика механизма.
- •3.4. Определение внешних сил на поршне.
- •3.5. Динамический анализ машинного агрегата.
- •3.5.1. Динамическая модель.
- •3.5.2. Определение приведенного момента инерции.
- •3.5.3. Определение приведенных моментов сил.
3.4. Определение внешних сил на поршне.
Движущие
силы на поршне определяются по заданной
механической характеристике в виде
индикаторной диаграммы p(SB),
т.е. графической зависимости давления
p
на поршне от перемещения SB.
Переносим индикаторную диаграмму на 1
лист поз.1, направив ось SB//OB,
а ось p//OB.
Масштабный коэффициент давления
![]() ,
где pmax
– заданное максимальное давление,
pmax=4,0
МПа, выбрана максимальная ордината
ymax=80мм.
,
где pmax
– заданное максимальное давление,
pmax=4,0
МПа, выбрана максимальная ордината
ymax=80мм.
Переносим из планов положений точки В поршня на ветви индикаторной диаграммы и расставляем номера точек диаграммы (поз.3 листа 1). При движении поршня вниз на рабочем ходу расширения в положениях 1,2,3,4,5,6,7 давление уменьшается от pmax до pк, а при движении поршня вверх на холостом ходу выхлопа и сжатия давление сначала равно нулю p=0, а потом возрастает до pc в положениях 8,9,10,11,12,13.
Величины
давлений
![]() ,
где yi
– замеренные ординаты диаграммы от оси
S
в мм. Величины движущих сил на поршне
,
где yi
– замеренные ординаты диаграммы от оси
S
в мм. Величины движущих сил на поршне
![]() ,
где П – площадь поршня,
,
где П – площадь поршня,
![]()
В расчетном положение №2.
![]() ;
;
![]() .
.
Результаты измерений yi и расчета давлений pi и сил F3 сводим в табл.3 Таблица 3
|
№ положения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Yi,мм |
36 |
80 |
64 |
41,5 |
24 |
15 |
8 |
0 |
1,5 |
11 |
23 |
32 |
78 |
|
Pi, МПА |
1,8 |
4,0 |
3,2 |
2,075 |
1,2 |
0,75 |
0,4 |
0 |
0,75 |
0,55 |
1,15 |
1,6 |
3,9 |
|
F3, Н |
11446,2 |
25436 |
20348,8 |
13194,9 |
7630,8 |
4769,25 |
2543,6 |
0 |
476,925 |
3497,45 |
7312,85 |
10174,7 |
24800,1 |
3.5. Динамический анализ машинного агрегата.
Необходимо
определить постоянную часть приведенного
момента инерции
![]() и момент инерции маховика Iм,
обеспечивающее плавное равномерное
вращение коленвала с заданным коэффициентом
неравномерности
и момент инерции маховика Iм,
обеспечивающее плавное равномерное
вращение коленвала с заданным коэффициентом
неравномерности
![]() .
Для упрощения расчетов используем
динамическую модель машины.
.
Для упрощения расчетов используем
динамическую модель машины.
3.5.1. Динамическая модель.
Наиболее простой динамической моделью машинного агрегата может быть одномассовая модель, представленная на рис.3.5.
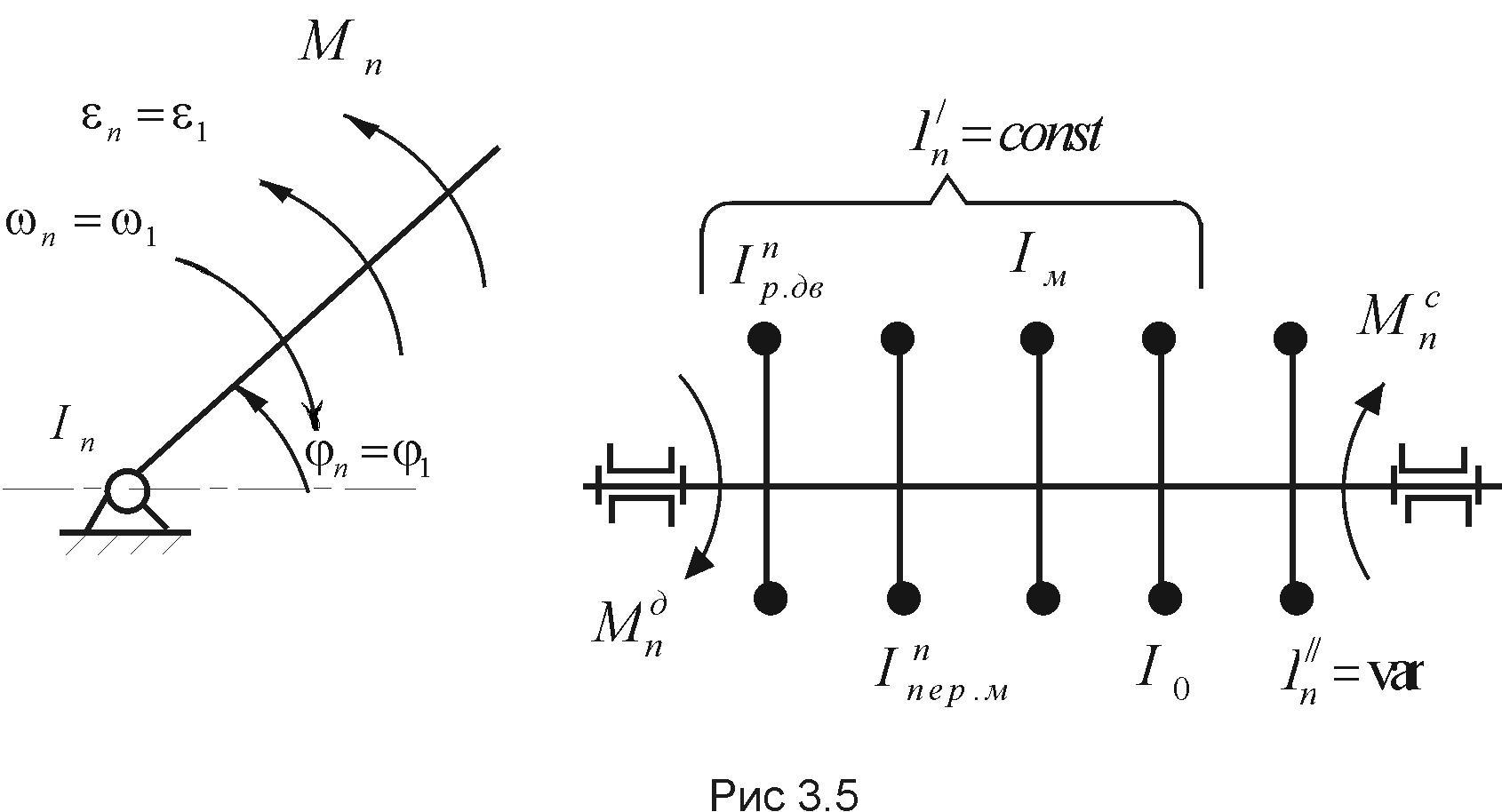
В
качестве такой модели рассматривается
условное вращающееся звено – звено
приведения, которое имеет момент инерции
Iп
относительно оси вращения (приведенный
момент инерции) и находится под действием
момента сил Mп
(приведенного момента сил). В свою
очередь,
![]() ,
где
,
где
![]() - приведенный момент движущих сил;
- приведенный момент движущих сил;
![]() - приведенный момент сил сопротивления.
Кроме того,
- приведенный момент сил сопротивления.
Кроме того,
![]() ,
где
,
где
![]() - постоянная составляющая приведенного
момента инерции. В величину
- постоянная составляющая приведенного
момента инерции. В величину
![]() входят собственный момент инерции
кривошипа (Io),
приведенные моменты инерции ротора
электродвигателя и передаточного
механизма (
входят собственный момент инерции
кривошипа (Io),
приведенные моменты инерции ротора
электродвигателя и передаточного
механизма (![]() ,
,![]() ),
а также момент инерции IМ
добавочной массы (маховика), причем
необходимость установки маховика
определяется на основании заданной
степени неравномерности движения звена
приведения.
),
а также момент инерции IМ
добавочной массы (маховика), причем
необходимость установки маховика
определяется на основании заданной
степени неравномерности движения звена
приведения.
Динамические
характеристики Мп
и Iп
должны быть такими, чтобы закон вращения
звена приведения был таким же, как у
главного вала машины (кривошипа 1
основного исполнительного рычажного
механизма), т.е.
![]() ,
,
![]() ,
,
![]() .
.
В курсовом проекте в качестве звена приведения принимаем кривошип 1.
