Глава 3. Кинематика точки

Положение точки в системе отсчета задается вектором положения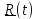 как функцией

времени, проведенным в точку из некоторого неподвижного в системе отсчета центра A:

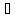
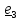
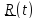
А

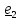
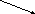
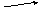
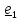
Траекторией называется кривая, по которой движется точка, скоростью 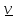– производная по

времени вектора положения R , ускорением 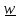- производная от вектора скорости

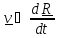
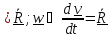. (3.1)

Из определения производной вектора следует, что вектор скорости направлен по

касательной к траектории. Собственно говоря, формулами (3.1) вся кинематика точки и

исчерпывается; все технические трудности связаны лишь с выбором системы координат.

Упражнение 1. Исходя из определения производной вектор-функции от скалярного

аргумента 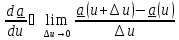показать, что

1) 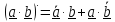(производная скалярного произведения)

2) 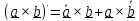(производная векторного произведения

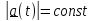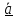
3) Если , то 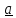 (продифференцировать квадрат модуля, равный ).

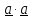2.1 Скорость и ускорение в декартовой системе координат.

В декартовой системе вектор положения задается в ви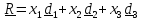де , где -

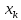координаты вектора, а 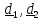, 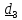– ортонормированный базис, т.е. базисные векторы

единичные и взаимно-перпендикулярные. В этом случае координаты равны проекциям

вектора на оси, задаваемые базисными векторами: .

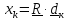Векторы скорости и ускорения равны

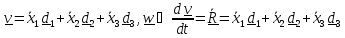
2.2 Скорость и ускорение в цилиндрической системе координат

Вектор положения точки задается как функция цилиндрических координат r,,z :

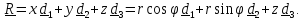(3.2)

В цилиндрической системе координат, как и в любой другой системе, вводятся базисные

векторы

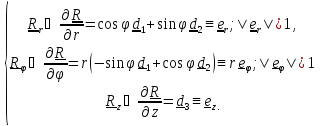(3.3)

Z

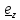
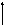
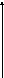
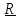
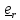
z

r Y

X

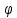
Базисные векторы направлены по касательным к так называемым координатным линиям –

линиям, получающимся при изменении только одной координаты.

Использование единичных базисных векторов 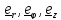удобно тем, что координаты

вектора в единичном базисе имеют ту же размерность, что и сам вектор.

Дифференцируя (3.2), получим с учетом (3.3)

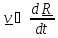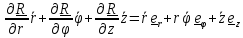= (3.4)

Дифференцируя (3.4) и учитывая, что 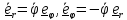, будем иметь

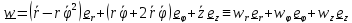(3.5)

Упражнение 2. Найти скорость и ускорение точки, движущейся по цилиндру .

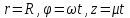(винтовая линия)

