Алгоритм 6. Сортировка последовательности чисел слиянием

Вход. Последовательность чисел x₁, x₂, …, x_n, где n=2^k, k  целое.

Выход. Последовательность y₁, y₂, …, y_n, являющаяся перестановкой входа и удовлетворяющая неравенствам y₁  y₂ …  y_n.

Метод. Задача сортировки элементов массива разбивается на две аналогичные задачи для массивов, каждый из которых представляет собой соответствующую половину исходного массива. Эту операцию осуществляет рекурсивная функция Sorting (Сортировка). Для слияния отсортированных массивов половинной длины используется функция Merge (Слияние), входом которой являются две упорядоченные последовательности S и T, а выходом  неубывающая последовательность элементов из S и T.

Программа 6.

// Программа сортирует элементы массива array в неубывающем порядке с помощью

// рекурсивной процедуры разбиения массива на две равные части и последующим

// слиянием отсортированных подмассивов

// NUM – размер исходного массива

#include <stdlib.h>

#include <stdio.h>

#include <io.h>

#include <alloc.h>

#include <time.h>

#define Mem_error {printf("Недостаточно памяти. \n"); exit(2);}

#define NUM 1024

int array[NUM], sorted[NUM];

void Sorting(int array[], int *in_min, int *in_max, int *sorted, unsigned size);

void Merge(int *out1, int *out2, unsigned size, int *sorted);

void main()

{

int *in_max, *in_min, *ptr_sorted;

unsigned index;

randomize();

// В этом месте должна стоять функция ввода массива array

// Задание границ массива

in_max=&array[NUM-1]; in_min=&array[0];

// Процедура сортировки

ptr_sorted=sorted;

Sorting(array, in_min, in_max, ptr_sorted, NUM);

} // Конец main

void Sorting(int array[], int *in_min, int *in_max, int *sorted, unsigned size)

// Функция сортировки массива с помощью техники рекурсии и слияния

{

unsigned size1;

int *max1, *min1, *max2, *min2, *out1, *out2;

if (size==1) *sorted=*in_min;

else

{

size1=size>>1; // Задание размера новых подмассивов

// Динамическое отведение памяти для новых подмассивов out1 и out2, которые

// в дальнейшем будут слиты в один выходной массив sorted

out1=(int far *)farcalloc(size1,sizeof(int));

if(out1==NULL) Mem_error // Проверка на наличие оперативной памяти

out2=(int far *)farcalloc(size1,sizeof(int));

if(out2==NULL) Mem_error // Проверка на наличие оперативной памяти

// Задание границ новых подмассивов

min1=in_min; min2=min1+size1;

max1=min2-1; max2=in_max;

// Сортировка новых подмассивов

Sorting(array, min1, max1, out1, size1);

Sorting(array, min2, max2, out2, size1);

// Слияние подмассивов

Merge(out1, out2, size1, sorted);

farfree(out1); farfree(out2); // Освобождение динамической памяти

}

} // Конец Sorting

Void Merge(int *out1, int *out2, unsigned size, int *sorted)

// Слияние двух отсортированных в неубывающем порядке подмассивов в один

{

unsigned ind1=0, ind2=0;

while ((ind1<size)&&(ind2<size))

{

if (out1[ind1] < out2[ind2]) *sorted++=out1[ind1++];

else *sorted++=out2[ind2++];

if (ind1==size)

while (ind2<size) *sorted++=out2[ind2++];

if (ind2==size)

while (ind1<size) *sorted++=out1[ind1++];

}

} // Конец Merge

Работа функции Merge состоит в выборе наименьшего из наименьших элементов сливаемых массивов и занесении его в выходной массив. После этого выбранный элемент удаляется из рассматриваемых массивов, и происходит сравнение следующих двух наименьших чисел. Поскольку сливаемые множества S и T сами уже упорядочены, то подобная процедура не требует числа сравнений, большего, чем сумма длин S и T без единицы.

Подсчёт числа сравнений в алгоритме 6 приводит к рекуррентным уравнениям

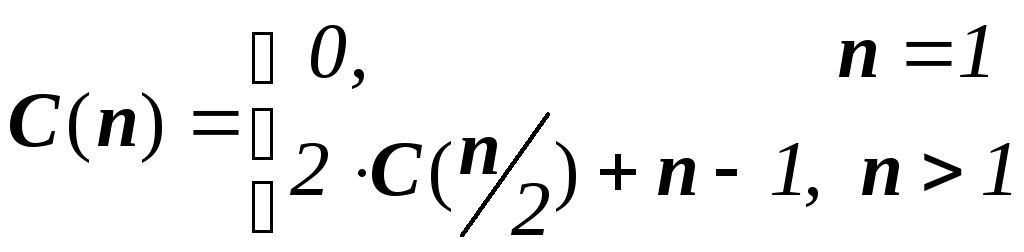, (1.10)

решением которых по теореме 1 является C(n)=O(nlogn). Для больших n сбалансированность размеров подзадач дала значительную выгоду.

Ещё один важный момент данной программы заключается в том, что функция Sorting использует динамическую память для сливаемых подмассивов, которая выделяется и освобождается по мере надобности. Данный приём используется очень часто для представления структур, связанных со списками и деревьями.

1.9 Динамическое программирование

Рекурсивная техника полезна, если задачу можно разбить на подзадачи за разумное время, а суммарный размер подзадач будет небольшим. Из теоремы 1 следует, что если сумма размеров подзадач равна an для некоторой постоянной a>1, то рекурсивный алгоритм, вероятно, имеет полиномиальную временную сложность. Однако если очевидное разбиение задачи размера n сводит её к n подзадачам размера n-1, то рекурсивный алгоритм, вероятно, имеет экспоненциальную сложность. В этом случае часто можно получить более эффективные алгоритмы с помощью техники, называемой динамическим программированием (dynamic programming).

Динамическое программирование вычисляет решения для всех подзадач. Вычисление идёт от малых подзадач к бóльшим, и ответы запоминаются в таблице. Преимущество этого метода состоит в том, что раз уж подзадача решена, её ответ где-то хранится и никогда не вычисляется заново. Попробуем рассмотреть данную технику на простом примере.

Пусть требуется вычислить произведение n матриц

M = M₁M₂…M_n,

где M_i  матрица с числом строк r_i-1 и числом столбцов r_i (размера r_i-1r_i). Порядок, в котором перемножаются данные матрицы, может существенно сказаться на общем числе операций, требуемых для вычисления M, независимо от алгоритма, используемого для умножения матриц.

Пример 1.7. Предположим, что для умножения матрицы размера (pq) на матрицу (qr) требуется pqr операций, как это бывает в «обычном» алгоритме, и рассмотрим произведение:

M = M₁  M₂  M₃,

(1020) (201) (150)

где внизу указаны размеры матриц. Если теперь вычислить M в порядке M₁(M₂M₃), то потребуется 11000 операций. Когда же произведение M будет вычислено в порядке (M₁M₂) M₃, то потребуется всего 700 операций.

Доказано, что процесс перебора всех возможных порядков, в которых можно вычислить рассматриваемое произведение n матриц, с целью минимизировать число операций имеет экспоненциальную сложность O(2ⁿ), что для больших n практически неприемлемо. Однако динамическое программирование приводит к алгоритму сложности O(n³). Пусть m_ij  минимальная сложность вычисления M_iM_i+1…M_j (1 i j n). Очевидно, что

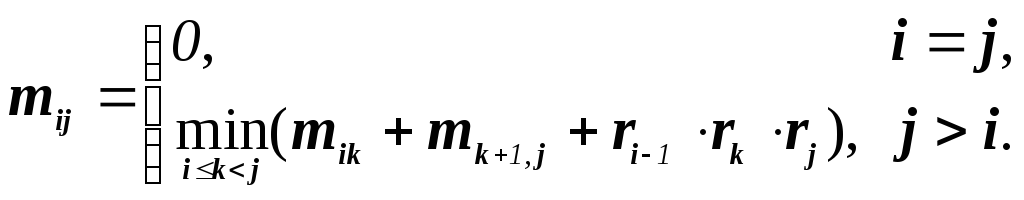(1.11)

Здесь m_ik  минимальная сложность вычисления M′=M_i+1M_i+2…M_k, а m_k+1,j  минимальная сложность вычисления M″=M_k+1M_k+2…M_j. Третье слагаемое равно сложности умножения M′ на M″. Поскольку матрица M′ имеет размер r_i-1 r_k, а матрица M″  размер r_k r_j. В (1.11) утверждается, что m_ij (j > i)  наименьшая из сумм этих трёх членов по всем возможным значениям k, лежащим между i и j-1.

При динамическом программировании m_ij вычисляются в порядке возрастания разнос­тей нижних индексов. Начинают с вычисления m_ii для всех i, затем m_i,i+1 для всех i, потом m_i,i+2 и т.д. При этом m_ik и m_k+1,j в (1.11) будут уже вычислены, до того, как приступают к вычислению m_ij. Это следует из того, что при i  k < j разность j-i должна быть больше k-i, а также и j(k+1).