Void Insert_Element(char New_Unit, unsigned Free, unsigned Position, char *Name, unsigned Next)

{

/* Функция вставляет новый элемент в список типа char на позицию вслед за

элементом с номером Position */

Name[Free]=New_Unit;

Next[Free]=Next[Position];

Next[Position]=Free;

} // Конец Insert_Element

Легко видеть, что время исполнения программы 2 не будет зависеть от размера списка.

Пример 1.2. Допустим, что нужно вставить в список (1.3) New_Unit после Unit2 и получить список

Unit1; Unit2; New_Unit, Unit3; Unit4

Если пятая ячейка в каждом массиве на рисунке 2 пуста, можно вставить New_Unit после Unit2, вызвав Insert_Element(New_Unit, 5, 3, Name, Next). В результате выполнения трёх операторов функции: Name[5]=New_Unit, Next[5]=4 и Next[3]=5. Получатся массивы, показанные на рисунке 3.

Номер индекса элемента	Name	Next
Рис. 3. Список со вставленным элементом New_Unit. 0		1
1	Unit1	3
2	Unit4	0
3	Unit2	5
4	Unit3	2
5	New_Unit	4

Для того чтобы удалить компоненту, следующую за компонентой в ячейке с номером Position можно выполнить следующий оператор Next[Position]= Next[Next[Position]]. При желании индекс удаленной компоненты можно поместить в список незанятых ячеек памяти.

Часто в один и тот же массив вкладываются несколько списков. Обычно один из этих списков состоит из незанятых ячеек; его называют свободным списком (Free List). Для добавления элемента к списку A можно так изменить функцию Insert_Element, что незанятая ячейка получалась путем удаления первой ячейки в свободном списке. При удалении элемента из списка A соответствующая ячейка возвращается в свободный список для будущего употребления.

Ещё две основные операции над списками  конкатенация (сцепление, concatenation) двух списков, в результате которой образуется единственный список, и обратная к ней операция расцепления (расщепления, split) списка, стоящего после некоторого элемента, результатом которой будут два списка. Конкатенацию можно выполнить за ограниченное (постоянной величиной) число шагов, включив в представление списка ещё один указатель. Этот указатель даёт индекс последней компоненты списка и тем самым позволяет обойтись без просмотра всего списка для определения его последнего элемента. Расцепление можно сделать за ограниченное (постоянной величиной) время, если известен индекс компоненты, непосредственно предшествующей месту расцепления.

Списки можно сделать проходимыми в обоих направлениях, если добавить ещё один массив, называемый Previous (Предыдущая). Значение Previous[Index] равно ячейке, в которой помещается тот элемент списка, который стоит непосредственно перед элементом из ячейки Index. Список такого рода называется дважды связанным (Doubly Linked List). Из дважды связанного списка можно удалить элемент или вставить в него элемент, не зная ячейку, где находится предыдущий элемент.

Со списком часто работают очень ограниченными приёмами. Например, элементы добавляются или удаляются только на конце списка. Иными словами, элементы вставляются и удаляются по принципу: «последний вошёл  первый вышел» (last-in first-out, LIFO). В этом случае список называют стеком (Stack) или магазином.

Часто стек реализуется в виде одного массива. Например, список

Unit1; Unit2; Unit3

можно хранить в массиве Name, как показано на рисунке 4

	Номер индекса эл-та	Name
Рис. 4. Реализация стека.	0	Unit1
	1	Unit2
Top 	2	Unit3

Переменная Top (Вершина) является указателем последнего элемента (Top of stack pointer), добавленного к стеку. Чтобы добавить (Затолкнуть – Push) новый элемент в стек значение Top увеличивают на 1, а затем помещают новый элемент в Name[Top]. (Поскольку массив Name имеет конечную длину l, перед попыткой вставить новый элемент следует проверить, что Top<l–1). Чтобы удалить (Вытолкнуть  Pop) элемент из вершины стека, надо просто уменьшить значение Top на 1. Здесь совсем необязательно физически стирать элемент, удаляемый из стека. Чтобы узнать, пуст ли стек, достаточно проверить, не имеет ли Top значение, меньшее нуля. Понятно, что время выполнения операций Push и Pop и проверка пустоты не зависят от числа элементов в стеке.

Другой специальный вид списка  очередь (Queue), т.е. список, в который элементы всегда добавляются с одного (переднего) конца, а удаляются с другого. Как и стек, очередь можно реализовать одним массивом. На рисунке 5 приведена очередь, содержащая список из элементов P, Q, R, S, T. Два указателя обозначают ячейки текущего переднего (Front) и заднего (Back) концов очереди. Чтобы добавить (Append) новый элемент к очереди, как и в случае стека, полагают Front++ и помещают новый элемент в Name[Front]. Чтобы удалить (Strip off) новый элемент из очереди, заменяют Back--. С точки зрения доступа к элементам эта техника основана на принципе «первый вошёл  первый вышел» (first in –first out; FIFO).

	Name
Back 	P
Рис. 5. Реализация очереди в виде одного массива.	Q
	R
	S
Front 	T

Поскольку массив Name имеет конечную длину, скажем l, указатели Front и Back рано или поздно доберутся до его концов. Если длина списка, представленного этой очередью, никогда не превосходит, то можно трактовать Name[0] как элемент, следующий за элементом Name[l–1].

Элементы, расположенные в виде списка, сами могут быть сложными структурами. Работая, например, со списком массивов, мы на самом деле не добавляем и не удаляем массивы, ибо каждое добавление или удаление потребовало бы времени, пропорционального размеру массива. Вместо этого мы добавляем или удаляем указатели массивов. Таким образом, сложную структуру можно добавить или удалить за фиксированное время, не зависящее от ее размера.

1.3. Представления множеств

«Множество есть многое, мыслимое нами как единое»

Г. Кантор

Обычно списки применяются для представления множеств. При этом объём памяти, необходимый для представления множества, пропорционален числу элементов. Время, требуемое для выполнения операций над множествами, зависит от природы операции. Например, пусть A и B  два множества. Операция AB требует времени, по крайней мере, пропорционального сумме размеров этих множеств, поскольку как список, представляющий A, так и список, представляющий B, надо просмотреть хотя бы один раз.

Подобным же образом операция AB требует времени, пропорционального сумме размеров множеств, поскольку надо выделить элементы, входящие в оба множества, и вычеркнуть один экземпляр каждого такого элемента. Если же A и B не пересекаются, можно найти AB за время, не зависящее от размера A и B. Для этого достаточно сделать конкатенацию списков, представляющих A и B. Задача объединения двух непересекающихся множеств усложняется, если необходимо быстро определять, входит ли данный элемент в данное множество.

Другой способ представления множества, отличный от представления его в виде списка,  представление в виде двоичного (битового) вектора. Пусть U  универсальное множество (т.е. все рассматриваемые множества являются подмножествами), состоящее из n элементов. Линейно упорядочим его. Подмножество SU представляется в виде вектора v_S из n битов, такого, что i-й разряд в v_S равен 1 тогда и только тогда, когда i-й элемент множества U принадлежит S. Будем называть v_S характеристическим вектором для S.

Представление в виде двоичного вектора удобнее тем, что можно определять принадлежность i-го элемента множества U данному множеству за время, не зависящее от размера данного множества. Более того, операции над множествами, такие как объединение и пересечение, можно осуществить как операции двоичной арифметики над двоичными векторами.

1.4. Графы

Определение. Граф G=(V,E) (graph) состоит из конечного непустого множества узлов V (node, vertex) и множества рёбер E. Если рёбра (arc) представлены в виде упорядоченных пар (v,w) узлов, то граф называется ориентированным (directed graph, oriented); v называется началом, а w  концом ребра (v,w). Если ребра  неупорядоченные пары (множества) (edge) различных вершин, также обозначаемые (v,w), то граф называется неориентированным (undirected graph). (В частности в ориентированном графе может быть ребро (a,a), а в неориентированном  нет).

Если в ориентированном графе G=(V,E) пара (v,w) принадлежит множеству ребер E, то узел w называется смежным с узлом v (incident, adjacent). Говорят, что ребро (v,w) идет из узла v в w. Число узлов, смежных с узлом v, называется полустепенью его исхода (out-degree).

Если (v,w)  ребро неориентированного графа G=(V,E), то считается, что (v,w)=(w,v), так что (w,v)  то же самое ребро. Узел w называется смежным с узлом v, если (v,w) (а значит, и (w,v)) принадлежит E. Степень узла  это число узлов, смежных с ним.

Путём в ориентированном или неориентированном графе называют последовательность ребер вида (v₁, v₂), (v₂, v₃), …, (v_n-1, v_n). Говорят, что путь идет из v₁ в v_n и имеет длину (n1).Часто такой путь представляют последовательностью v₁, v₂, …, v_n узлов, лежащих на нём. В вырожденном случае один узел обозначает путь длины 0, идущий из этого узла в него же. Путь называется простым, если все ребра и все узлы на нём, кроме, может быть, первого и последнего узла, различны. Цикл  это простой путь длины не менее 1, который начинается и кончается в одном и том же узле.

Известно несколько представлений графа G=(V,E). Один из них  матрица смежностей, т.е. матрица A размера ║V║║V║ (║X║ обозначает здесь число элементов множества X), состоящая из 0 и 1, в которой A[i,j]=1 тогда и только тогда, когда есть ребро из узла i в узел j. Представление в виде матрицы смежностей удобно для тех алгоритмов на графах, которым часто нужно знать, есть ли на графе данное ребро, ибо время, необходимое для определения наличия ребра, фиксировано и не зависит от ║V║ и ║E║. Основной недостаток применения матрицы смежностей заключается в том, что она занимает память объёма ║V║² даже тогда, когда граф содержит только O(║V║) ребер. Уже начальное заполнение матрицы смежностей посредством «естественной» процедуры требует времени O(║V║²), что сводит на нет алгоритмы сложности O(║V║) при работе с графами, содержащими лишь O(║V║) рёбер.

Интересной альтернативой является представление строк и (или) столбцов матрицы смежностей в виде двоичных векторов. Такое представление может способствовать значительной эффективности алгоритмов на графах.

Ещё одно возможное представление графа  с помощью списков. Списком смежностей (list of incident nodes) для узла v называется список всех узлов w, смежных с v. Граф можно представить с помощью ║V║ списков смежностей, по одному для каждого узла.

Пример 1.3. На рисунке 6,а изображен ориентированный граф, содержащий четыре узла, на рисунке 6,б  его матрица смежностей. На рисунке 6,в показаны четыре списка смежностей, по одному для каждого узла. Например, из узла 1 в узлы 2 и 4 идут ребра, так что список смежностей для 1 содержит компоненты 2 и 4, связанные в смысле рисунка 1.

Табличное представление списков смежностей приведено на рисунке 6,г. Каждая из первых четырёх ячеек в массиве Next содержит указатель на первый узел списка смежностей, а именно Next[i] указывает на первый узел списка смежностей для узла i. Next[3]=0, поскольку в списке смежностей для узла 3 нет узлов. Остальные составляющие массива Next представляют собой рёбра графа. Массив End содержит узлы из списков смежностей.

1

21

	1	2	3	4
1	0	1	0	1
2	0	0	1	0
3	0	0	0	0
4 3 4	0	1	1	0

а б

4 0 Node 1			End	Next
2 3 Node 2 0 Nnodes		1		5
		2		7
		3		0
		4		8
Node 3 3 0 Node 4 Empty list 2 aarcs		5	2	6
		6	4	0
		7	3	0
		8	2	9
		9	3	0

в г

Рис. 6.

Таким образом, список смежностей узла 1 начинается в ячейке 5, ибо Next[1]=5, End[5]=2; это показывает, что есть ребро (1,2). Равенства Next[5]=6 и End[6]=4 означают, что есть ребро (1,4), а Next[6]=0  что больше нет рёбер, начинающихся в 1.

Представление графа в виде списков смежностей требует памяти порядка ║V║+║E║. Им часто пользуются, когда ║E║«║V║².

Если граф неориентированный, то каждое ребро (v,w) представляется дважды: один раз в списке смежностей для v и один раз в списке смежностей для w. В этом случае можно добавить новый массив, называемый Link (Связь), чтобы коррелировать оба экземпляра неориентированного графа. Таким образом, если i  ячейка, соответствующая узлу w в списке смежностей для v, то Link[i]  ячейка, соответствующая узлу v в списке смежностей для w.

Если необходимо с удобством удалять ребра из неориентированного графа, то списки смежностей можно связать дважды (как описано в разделе 1.2). Это обычно бывает нужно потому, что даже если удалять всегда ребро (v,w), стоящее первым в списке смежностей узла v, всё равно может оказаться, что ребро, идущее в обратном направлении, стоит в середине списка смежностей узла w. Чтобы быстро удалить ребро (v,w) из списка смежностей для w, надо уметь быстро находить ячейку, содержащую предыдущее ребро в списке смежностей, что делает подобное представление очень удобным для использования его в машинных программах для различных приложений.

1.5. Деревья

Теперь введем в рассмотрение важный вид ориентированных графов  деревья (tree) и рассмотрим структуры данных, пригодные для их представления.

Определение. Ориентированный граф без циклов называется ориентированным ациклическим (acyclic) графом. (Ориентированное) дерево (иногда его называют корневым деревом (sink tree))  это ориентированный ациклический граф, удовлетворяющий следующим условиям:

• имеется в точности один узел, называемый корнем (root), в который не входит ни одно ребро;

• в каждый узел, кроме корня, входит ровно одно ребро;

• из корня к каждому узлу идет путь (который, как легко показать, единственен).

Ориентированный граф, состоящий из нескольких деревьев, называется лесом (forest). Леса и деревья  столь часто встречающиеся случаи ориентированных ациклических графов, что для описания их свойств стόит ввести специальную терминологию.

Определение. Пусть F=(V,E)  граф, являющийся лесом. Если (v,w) принадлежит E, то v называется отцом узла w (father node, parent node), а w  сыном или потомком (child node, descendant) узла v. Более того, если vw, то v называется подлинным предком (proper ancestor) узла w, а w  подлинным потомком (proper descendant) узла v. Узел без подлинных потомков называется листом (leaf). Узел v и его потомки вместе образуют поддерево (subtree) леса F, и узел v называется корнем этого поддерева.

Глубина узла (depth of a vertex) v в дереве  это длина пути из корня в v. Высота узла (height of a vertex) в дереве  это длина самого длинного пути из v в какой-нибудь лист. Высотой дерева называется высота его корня. Уровень узла (level of a vertex) v в дереве равен разности высоты дерева и глубины узла v. Например, на рисунке 7,а узел 3 имеет глубину 2, высоту 0 и уровень 1.

Упорядоченным деревом (ordered tree) называют дерево, в котором множество сыновей каждого узла упорядочено. Далее будем считать, что множество сыновей каждого узла упорядоченно слева направо. Двоичным (бинарным) деревом (binary tree) называется такое упорядоченное дерево, что

1. каждый сын произвольного узла идентифицируется либо как левый сын (left son), либо как правый сын (right son);

2. каждый узел имеет не более одного левого сына и не более одного правого сына.

Поддерево T_l, корнем которого является левый сын узла v (если такое существует), называется левым поддеревом узла v. Аналогично поддерево T_r, корнем которого является правый сын узла v (если такое существует), называется правым поддеревом узла v. Все узлы в T_l расположены левее всех узлов в T_r.

Двоичное дерево представляется обычно в виде двух массивов Leftson и Rightson. Пусть все узлы двоичного дерева занумерованы целыми числами от 1 до n. В этом случае Leftson[i]=j тогда и только тогда, когда узел с номером j является левым сыном узла с номером i. Rightson[i] определяется аналогично.

Пример 1.4. Двоичное дерево и его представление показано на рисунке 7. 

Определение. Двоичное дерево называется полным (complete tree), если для некоторого целого числа k каждый узел глубины меньшей k имеет как левого, так и правого сына, и каждый узел глубины k является листом. Полное двоичное дерево имеет ровно 2^k+1-1 узлов.

Полное двоичное дерево высоты k часто представляется одним массивом. В позиции 1 этого массива находится корень. Левый сын узла в позиции i расположен в позиции 2i, а его правый сын  в позиции 2i +1. Отец узла, находящегося в позиции i1, расположен в позиции i/2, (где xобозначают наибольшее целое, не превосходящее x).

Многие алгоритмы, использующие деревья, часто проходят дерево (посещают каждый узел) в некотором порядке. Известно несколько систематических способов сделать это. Рассмотрим три широко распространенных из них: прохождение дерева в прямом порядке, обратном и внутреннем. Прохождение дерева (traversal of a tree).

1	Leftson	Rightson
1	2	6
2 6 3 4 5 7 8 9 2	3	4
3	0	0
4	0	5
5	0	0
6	7	8
7	0	0
8	0	9
9	0	0

а б

Рис. 7.

Определение. Пусть T – дерево с корнем r и сыновьями v₁,…, v_k, (k0) При k=0 это дерево состоит из единственного узла r.

Прохождение дерева T в прямом порядке (preorder) определяется следующим правилом:

1. посетить корень r;

2. посетить в прямом порядке поддеревья с корнями v₁,…, v_k в указанной последовательности.

Прохождение дерева T в обратном порядке (postorder) определяется следующим правилом:

1. посетить в обратном порядке поддеревья с корнями v₁,…, v_k в указанной последовательности,

2. посетить корень r.

Прохождение дерева T во внутреннем порядке (inorder) определяется следующим правилом:

1. посетить во внутреннем порядке левое поддерево корня (если оно существует);

2. посетить корень;

3. посетить во внутреннем порядке правое поддерево корня (если оно существует).

1

1

1

2

6

2

2

6

6

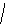
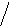
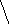
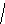
3

3

3

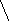
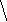
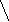
а б в

4

5

7

8

8

8

4

4

5

5

7

7

Рис. 8

Пример 1.5. На рисунке 8 изображено двоичное дерево, узлы которого пронумерованы в соответствии с прохождением его в прямом порядке (а), обратном (б) и внутреннем (в). 

Если все узлы занумерованы в порядке посещения, то рассмотренные нумерации обладают рядом интересных свойств.

При нумерации в прямом порядке все узлы поддерева с корнем r имеют номера, не меньшие r. Если D_r  множество потомков узла r, то v будет номером некоторого узла из D_r тогда и только тогда, когда r v r+║D_r║. Поставив в соответствие каждому узлу v номер в прямом порядке и количество его потомков, легко определить, является ли некоторый узел w потомком для v. После того, как номера присвоены (в соответствии с прямым порядком) и вычислено количество потомков каждого узла, на вопрос, является ли w потомком для v, можно ответить за фиксированное время, не зависящее от размера дерева. Номера, соответствующие обратному порядку, обладают аналогичным свойством.

Номера узлов двоичного дерева, соответствующие внутреннему порядку, обладают тем свойством, что номера узлов в левом поддереве для v меньше v, а в правом поддереве больше v. Таким образом, чтобы найти узел с номером w, надо сравнить w с корнем r. Если w=r, то искомый узел найден. Если w<r, то надо повторить процесс для левого поддерева; если w>r, то повторить процесс для правого поддерева.

Определение. Неориентированным деревом называется неориентированный ациклический связанный (два любые узла соединены путём) граф. Корневое неориентированное дерево – это неориентированное дерево, в котором один узел выделен в качестве корня.

1.6. Рекурсия

Процедуру, которая прямо или косвенно обращается к себе, называют рекурсивной. Применение рекурсии (recursion) часто позволяет дать более прозрачные и сжатые описания алгоритмов, чем это было бы возможно без рекурсии.

Рассмотрим определение прохождения двоичного дерева во внутреннем порядке, данное в разделе 1.5.

Идея прохождения дерева во внутреннем порядке заключается в следующем. Находясь в каком-то узле v, необходимо сначала проверить, есть ли у данного узла левый сын. Если таковой нашёлся, то нужно запомнить данный узел v и двинутся к левому сыну. С левым сыном описанная выше процедура повторяется, и т.д. Если же левого сына у узла v нет, то нужно присвоить этому узлу текущий номер и двинуться к правому сыну узла v, с которым опять требуется повторить сначала всю описанную процедуру. Если же сыновей у узла v нет, то необходимо вернуться к его предку на один уровень вверх. Далее процедура повторяется. Двигаться вниз по дереву нетрудно, но чтобы обеспечить возможность вернуться к предку, надо запомнить всех предков в стеке.

Один из возможных алгоритмов, реализованный на языке C, представлен ниже.

Алгоритм 3.1 нумерации узлов двоичного дерева в соответствии с внутренним

порядком.

Вход. Двоичное дерево, представленное массивами Leftson и Rightson.

Выход. Массив, названный Number (Номер), такой, что Number[i] – номер узла i во внутреннем порядке.

Метод. Кроме массивов Leftson, Rightson и Number, алгоритм использует глобальную переменную counter (Счет), значение которой  номер очередного узла в соответствии с внутренним порядком. Начальным значением counter является 1. Параметр node (Узел) вначале равен корню. При прохождении дерева в стеке Vertex запоминаются все узлы, которые ещё не были занумерованы и которые лежат на пути из корня в узел, рассматриваемый в данный момент. При переходе из узла v к его левому сыну узел v запоминается в стеке. После нахождения левого поддерева для v узел v нумеруется и выталкивается из стека. Затем нумеруется правое поддерево для v.

При переходе из v к его правому сыну узел v не помещается в стек, поскольку после нумерации правого поддерева не нужно возвращаться в v. Более того, нужно вернуться к тому предку узла v, который еще не занумерован (т.е. к ближайшему предку w узла v, такому, что v лежит в левом поддереве для w). После чего процедура повторяется для выбранного правого сына текущего узла.

Программа 3.1 нумерации узлов двоичного дерева в соответствии с внутренним

порядком.

// Программа прохождения бинарного дерева во внутреннем порядке без рекурсии

// STACK_SIZE – число узлов в дереве, ROOT – номер корня.

#include <stdio.h>

#include <io.h>

#include <stdlib.h>

#define STACK_SIZE 10

#define ROOT 1

// Определение структур стека и бинарного дерева

typedef struct {

unsigned name[STACK_SIZE];

unsigned top;

} stack;

stack vertex;

typedef struct {

unsigned leftson[STACK_SIZE];

unsigned rightson[STACK_SIZE];

} binary_tree;

binary_tree graph;

unsigned number[STACK_SIZE], counter=1, node=ROOT, index;