4.1. Итерационные методы Якоби и Зейделя.

Рассмотрим простейшие итерационные методы решения СЛАУ, - методы Якоби (простой итерации) и Зейделя. Будем рассматривать систему

Ах = f,

(4.1)

где

(4.2)

- матрица, имеющая обратную матрицу, х = (х₁, х₂, …, х_n)^T, f = (f₁, f₂, …, f_n)^T – соответственно векторы-столбцы неизвестных и правых частей.

Начнем рассмотрение с метода Якоби. Будем считать, что все а_ii  0, i = 1, 2, …, n, где а_ii – элементы матрицы А, лежащие на главной диагонали. Преобразуем систему (4.1) к виду

(4.3)

В равенстве (4.3) значение суммы считается, как это принято, равным нулю, если значение верхнего предела суммирования меньше значения нижнего предела суммирования.

Далее верхний индекс будет указывать номер итерации (приближения), например,

Зададим произвольным образом начальное приближение номера к = 0, например так

Исходя из равенства (4.3), итерационное равенство (формулу) метода Якоби запишем так

, к = 0, 1, 2, …

(4.4)

Окончание итераций определяется:

1) по числу итераций, заданному заранее (максимальному числу итераций);

2) по величине так называемой стабилизации

 > 0 заданное число, близкое к 0;

3) по убыванию нормы вектора невязки на k-ой итерации, где

rk = f – Axk,

(4.5)

в заданное число раз по сравнению с нормой вектора начальной невязки , т.е. при выполнении неравенства

Напомним, что в качестве нормы вектора r^k можно взять величины: или k = = 0,1,…

С вычислительной точки зрения способ 3) хотя и более громоздкий, по сравнению со способами 1) и 2), однако, он дает наиболее объективную информацию о погрешности полученного решения.

Идея метода Зейделя состоит в том, чтобы найденные значения использовать для вычисления , усовершенствовав формулу (4.4) так:

(4.6)

4.2. Каноническая форма итерационных методов.

Для исследования сходимости итерационных методов, т.е. установления справедливости равенства где х – точное решение системы (2.1), удобнее записывать эти методы в матричной, а не в координатной форме.

Представим матрицу А в виде суммы трех матриц

А = А^- + D + A⁺, где

- диагональная часть матрицы А.

Очевидно, метод Якоби с использованием введенных обозначений в векторной форме принимает вид

х^k+1 = -D^-1(А⁺ + А^-)х^k + D^-1  f,

где D^-1 – матрица, обратная к матрице D

Метод Якоби еще можно записать так

D(хk+1 – xk) +Axk = f.

(4.7)

Аналогичным образом из соотношений (4.6) можно получить представление метода Зейделя в векторной форме

(D + А-)(хk+1 – xk) + Axk = f.

(4.8)

Далее мы увидим, что векторные равенства (4.7) и (4.8) являются частными случаями так называемой канонической формы одношаговых (двухслойных) итерационных схем вида

(4.9)

где В – квадратная невырожденная матрица nn, называемая стабилизатором, _k+1 – число, называемое итерационным параметром.

Матрица А называется положительно определенной, если скалярное произведение (Ах, х) > 0 для всех ненулевых векторов, или что то же самое (х^Т, Ах) > 0.

Сформулируем теорему, принадлежащую А.А. Самарскому.

Теорема. Пусть А – симметричная положительно определенная матрица, _k+1   > 0, и пусть выполнено неравенство для любого ненулевого вектора х из n-мерного пространства.

((В – 0,5А)х, х) > 0.

Тогда итерационный метод (4.9) сходится, т.е.

Покажем, как использовать данную теорему для доказательства сходимости, например, метода Зейделя.

Сравнивая (4.8) и (4.9) приходим к равенствам

В = D + А^-,  = 1.

Таким образом, если А = А^Т и А – положительно определенная матрица, то при условии выполнения неравенства В – 0,5 А > 0, что является краткой формой записи неравенства относительно скалярных произведений

((В – 0,5 А)х, х) > 0, x  Rⁿ,

метод Зейделя сходится.

Заметим, что

В – 0,5 А = В – 0,5 А = D + А- - 0,5(А+ + D + А-) = = 0,5  D + 0,5(А- - А+).

(4.10)

Нетрудно проверить, что для любого n-мерного вектора х (х  Rⁿ)

((A- - A+)x, x) = 0.

(4.11)

C другой стороны, из неравенства (Ах, х) > 0 x  Rⁿ вытекает неравенство

(Dх, х) > 0

(4.12)

В самом деле, выберем х = (0, … 0, _i, 0 … 0) где _i  0. Тогда

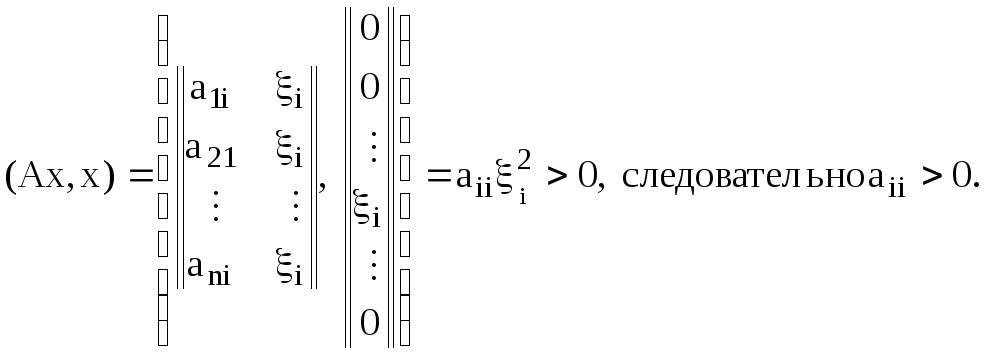
Поскольку i – любое, то все а_ii > 0, i = 1, 2, …, n. Значит справедливо неравенство (4.12). В силу (4.11) и (4.12) из (4.10) имеем

В – 0,5 А > 0.