6 Методы приближения функций

Интерполяция в общем понимании - это нахождение промежуточных значений величины по некоторым известным ее значениям.

Интерполяция применяется во многих задачах, связанных с вычислениями, например:

1) восстановить функцию y(x) для всех значений x на отрезке [a,b], если известны ее значения в некотором конечном числе точек этого отрезка;

2) заменить функцию близким выражением, удобным для проведения вычислений, если исходная функция представлена выражением, трудным для вычислений;

3) выполнить субтабулирование, т.е. сгущение таблицы значений;

4) решить задачу обратного интерполирования, т.е. по заданной таблице y_i=y(x_i) значений функции найти x как функцию от y.

В результате возникает следующая математическая задача: пусть на отрезке [a,b] задана сетка , в ее узлах заданы значения функций y(x), равные y(x₀) = y₀, y(x₁) = y₁, …, y(x_i) = y_i, …, y(x_n) = y_n. Требуется построить интерполянту, т.е. функцию (x), совпадающую с функцией y(x) в узлах сетки

(xi) = yi, i = 0, 1, …, n .

(6.1)

Интерполянта строится, как правило, в виде линейной комбинации некоторых линейно независимых на отрезке [a,b] элементарных функций

{_k(x)}, k = 0, 1, …, n;

(6.2)

где c_k -неизвестные коэффициенты. Из условия (6.1) для определения этих коэффициентов получим систему (n+1) уравнений

(6.3)

Система функций {_k(x)}, k = 0, 1, …, n такова, что при любом выборе сетки узлов отличен от нуля определитель системы (6.3)

Поэтому из системы (6.3) однозначно определяются коэффициенты с_к.

В качестве функции (x) в дальнейшем будем брать алгебраический многочлен степени n, т.е. (x) = P_n(x). В этом случае интерполяция называется алгебраической. Алгебраическая интерполяция является наиболее распространенной, т.к. многочлены легко вычисляются, их легко дифференцировать и интегрировать. В этом случае в качестве системы линейно независимых функций {_k(x)} обычно выбирают следующую систему: _k(x) = x^k, k = 0, 1, …, n.

Двух различных интерполяционных полиномов одной и той же степени n существовать не может. Действительно, предположив обратное, приходим к выводу, что разность двух таких многочленов, являющаяся многочленом степени не выше n , имеет (n+1) корней, следовательно, равна тождественно нулю.

6.1. Интерполяционный полином Лагранжа и Ньютона.

Интерполяционный полином Лагранжа.

Поставим следующую задачу: построить многочлен P_n(x) степени n, который в (n+1) данной точке x₀, x₁, ... x_n , называемых узлами интерполяции, принимает данные значения y₀, y₁, ... y_n .

В данном случае речь идет о построении многочлена P_n(x) степени n, который в определенном смысле "близок" к исходной функции y(x). Известно, что любая непрерывная [a,b] функция y(x) может быть хорошо приближена полиномом P_n(x). Имеет место следующий результат.

Теорема. Для любого  > 0 существует полином P_n(x) степени n = n(), такой, что

.

Если в качестве базиса {_k(x)} взять базис, состоящий из функций I, x, x², ... , xⁿ , то интерполяционный полином имеет вид

.

(6.4)

Используя условия интерполяции (6.1), имеем для определения коэффициентов c_k систему уравнений

c₀ + c₁x₀ + … + c_n = y₀

c₀ + c₁x₁ + … + c_n = y₁;

………….

c₀ + c₁x_n + … + c_n = y_n.

Определителем этой системы является отличный от нуля определитель Вандермонда

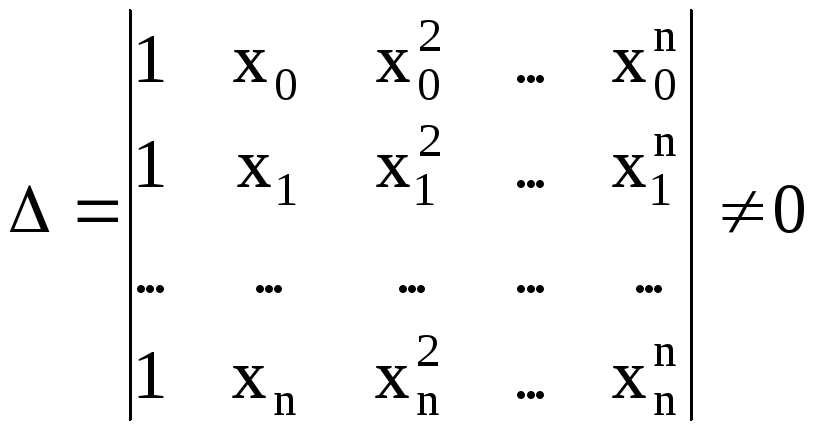
Отсюда следует единственность представления (6.4).

Более удобным для вычислений является базис полиномов Лагранжа {_k(x)} степени n относительно x, удовлетворяющий следующим условиям:

.

Искомый многочлен запишется согласно представлению (6.2) в виде

.

(6.5)

Поскольку x₀, x₁, ... , x_k-1, x_k+1, ... , x_n - нули многочлена _k(x), а также, учитывая, что _k(x_k) = 1, имеем

.

(6.6)

Формула (6.5) с учетом (6.6) имеет вид

.

(6.7)

или

.

(6.8)

Многочлен, определенный формулой (6.7), называется интерполяционным полиномом Лагранжа, а элементы базиса {_k(x)} из формулы (6.6) - коэффициентами Лагранжа.

Формулу (6.7) можно записать в более компактной форме, если ввести обозначение

(x) = (x – x₀) (x – x₁) … (x – x_n).

Так как

'(x_k) = (x_k – x₀) (x_k – x₁) … (x_k – x_k-1) (x_k – x_k+1) … (x_k – x_n),

то

_k(x) = (x) / ((x – x_k)  (x_k)) .

Тогда

.

(6.9)

Итак, в результате интерполирования функции мы заменили эту функцию полиномом (6.9), совпадающим с ней в узлах интерполяции x₀, x₁,...,x_n. В остальных точках отрезка [a, b] разность R(x) = y(x) –

– P_n(x) называется остаточным членом интерполяции, представляющим погрешность метода, определяемую следующей теоремой.

Теорема. Если функция y(x) имеет на отрезке [a,b] непрерывные производные до (n+1)-го порядка включительно, то остаточный член интерполяции R(x) определяется формулой

R(x) = y⁽ⁿ⁺¹⁾()(x)/(n+1)!, a <  < b.

Число арифметических операций для вычисления значений функции y(x) по формуле (6.7) равно Q = 4n (n + 1)  4n².

Рассмотрим случай равноотстоящих узлов интерполяции, т.е. когда x_i – x_i-1 = h, i = = . Сделав замену x=x₀+ht, имеем при t₀=0,t₁=1,...,t_n=n, x-x_k=h(t-k),

(x) = hⁿ⁺¹t(t – 1) … (t – n), (x_k) = (-1)^n-kk!(n – k)!h^k.

Тогда выражение (6.9) для интерполяционного многочлена Лагранжа принимает вид

.

Интерполяционный полином Ньютона.

Пусть y₀ = y(x₀), y₁ = y(x₁), …, y_n = y(x_n) - значения функции y(x) в узлах интерполяции. Тогда разности

y₀ = y₁ – y₀, y₁ = y₂ – y₁, …, y_n-1 = y_n – y_n-1

называются конечными разностями первого порядка или просто первыми разностями.

Разностями второго порядка или вторыми разностями называются разности первых разностей, т.е.

²y₀ = y₁ - y₀, ²y₁ = y₂ - y₁, …, ²y_n-2 = y_n-1 - y_n-2.

Аналогично определяются последующие разности. Например, разность (к+1)-го порядка получается из разности k-го порядка по формулам

^k+1y₀ = ^ky₁ - ^ky₀, ^k+1y₁ = ^ky₂ - ^ky₁ .

Разности высших порядков выражаются через y_i следующими формулами:

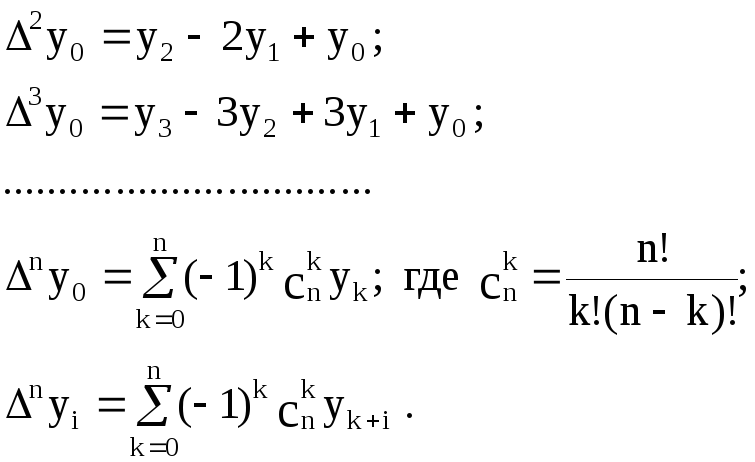
Введем так называемые разделенные разности .

Разделенные разности первого порядка определяются формулой

y(x_i, x_j) = (y_i – y_j) / (x_i – x_j).

Например,

y(x₁, x₀) = (y₁ – y₀)/(x₁ – x₀) = y₀/h₁, где h₁ = x₁ – x₀,

y(x₂, x₁) = (y₂ – y₁)/(x₂ – x₁) = y₁/h₂, где h₂ = x₂ – x₁, и т.д.

Разделенные разности второго порядка определяются формулой

y(x_i, x_j, x_k) = [y(x_i, x_j) – y(x_j, x_k)] / (x_i – x_k).

Разделенные разности k-го порядка определяются формулой

y(x_k, x_k-1, …, x₁, x₀) = [y(x_k, x_k-1, …, x₁) – y(x_k-1, …, x₀)] / (x_k – x₀).

В случае равностоящих узлов с шагом h для разделенных разностей имеем формулы:

y(x₁, x₀) = y₀ / h, y(x₂, x₁) = y₁ / h, …, y(x_n, x_n-1) = y_n-1 / h;

y(x₂, x₁, x₀) = ²y₀ / 2!h², y(x₃, x₂, x₁) = ²y₁ / 2!h, …;

y(x_k, x_k-1, x₀) = ^ky₀ / k!h.

Если у(x)=P_n(x) - полином степени n , то для него первая разделенная разность P(x, x₀) = (P(x) – P(x₀)) / (x – x₀) - есть полином степени (n-1), вторая разделенная разность P(x,x₀,x₁) - полином степени (n-2), так что разделенная разность (n+1)-го порядка равна нулю.

Разделенные разности располагаются по схеме:

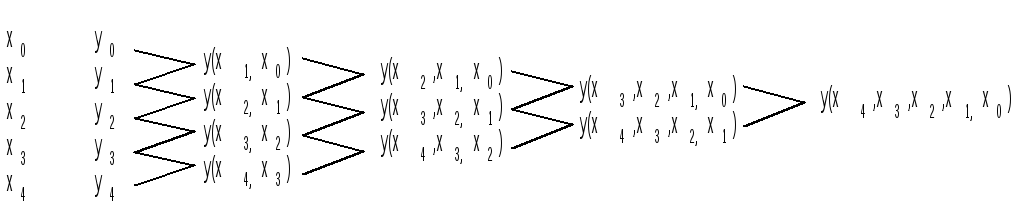
Рассмотрим первую разделенную разность для функции y(x)

y(x, x₀) = (y(x) – y₀) / (x – x₀), откуда y(x) = y₀ + (x – x₀) y(x, x₀).

Далее имеем

y(x, x₀) = y(x₀, x₁) + (x – x₁) y(x, x₀, x₁),

y(x, x₀, x₁) = y(x₀, x₁, x₂) + (x – x₂) y(x, x₂, x₁, x₀)

и т.д. Отсюда получаем формулу

y(x) = y₀ + (x – x₀) y(x₀, x₁) + (x – x₀) (x – x₁) y(x₀, x₁, x₂) + … +

+ (x – x₀) (x – x₁) … (x – x_n-1) y(x₀, x₁, …, x_n) +

+ (x – x₀) … (x – x_n) y(x, x₀, …, x_n)

или

y(x) = P_n(x) + (x – x₀) (x – x₁) … (x – x_n) y(x, x₀, x₁, …, x_n),

где

.

(6.10)

Если положить в формуле (6.10) x = x_k, k = 0, 1, …, n, получим P_n(x_k) = y_k.

Следовательно, полином (6.10) является интерполяционным полиномом, построенным по (n+1) узлам x₀, x₁, ... , x_n . Он называется интерполяционным многочленом Ньютона.

В силу того, что любой k-й член полинома Ньютона (6.10) зависит только от к первых узлов интерполяции и от значений функции в этих узлах, добавление новых узлов вызывает лишь добавление в формуле (6.10) новых членов без изменения первоначальных, в этом состоит существенное, с точки зрения организации вычислений, преимущество полинома Ньютона по сравнению с полиномом Лагранжа.

Формулу для полинома Ньютона (6.10) можно переписать в следующем виде:

В данном случае базис состоит из функций вида

,

В этом случае c_k = y(x₀, x₁, ..., x_k), После вычисления коэффициентов c_k , значения полинома Ньютона в точке x удобно вычислять по схеме Горнера

P_n(x) = y₀ + (x – x₀)[y(x₀, x₁) + (x - x₁)[y(x₀, x₁, x₂) + …]].

Вычисление значений x полинома P_n(x) (после вычисления c_k) требует n умножений и 2n сложений (или вычитаний), т.е. Q = 3n.

На практике избегают пользоваться интерполяционными многочленами высоких степеней. Объясняется это тем, что с ростом числа узлов сетки погрешность интерполирования f(x) – L_n(x) может не только не уменьшаться, но и в некоторых случаях постепенно расти с увеличением n. В этом случае говорят, что интерполяционный процесс расходится. Например, последовательность многочленов Ньютона, построенных для непрерывной функции f(x) = x на отрезке [-1, 1] не сходится к функции f(x) = x ни в одной точке отрезка [-1, 1] кроме точек –1, 0, 1. Поэтому более предпочтительной является интерполяция сплайнами, к рассмотрению которой мы переходим.
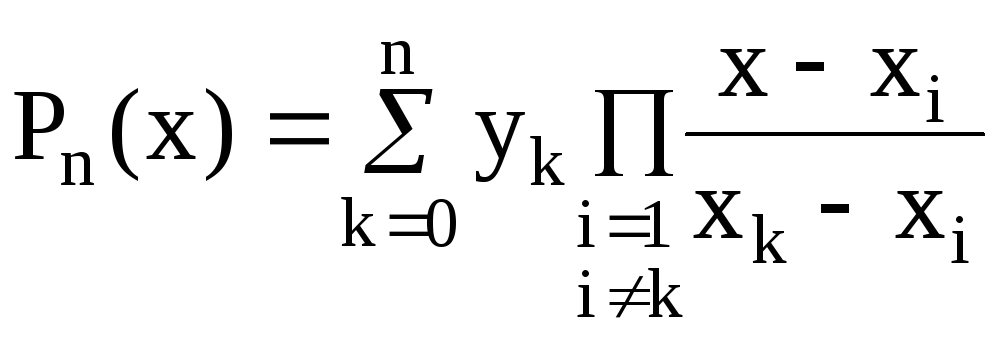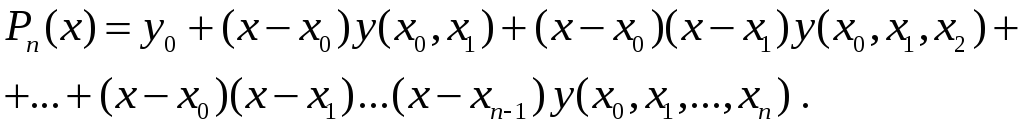