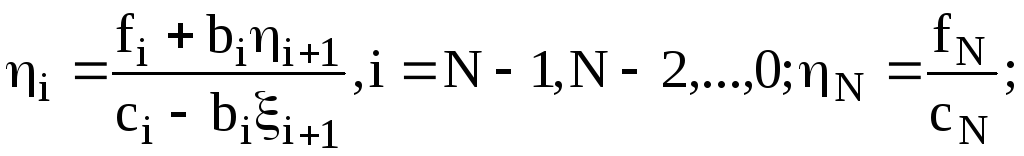- •Таганрогский государственный радиотехнический университет
- •Введение
- •1 Численное интегрирование
- •1.1 Основные методы численного интегрирования
- •1.2 Пример выполнения лабораторной работы №1
- •1.3 Варианты заданий к лабораторной работе №1
- •2 Методы решения нелинейных уравнений
- •2.1 Метод половинного деления
- •2.2 Метод хорд (метод линейной интерполяции)
- •2.3 Метод секущих
- •2.4 Метод Ньютона
- •2.5 Пример выполнения лабораторной работы №2
- •2.6 Варианты заданий к лабораторной работе №2
- •3 Прямые методы решения систем линейных алгебраических уравнений
- •3.1 Метод Гаусса для решения систем линейных алгебраических уравнений.
- •3.2. Алгоритм lu-разложения.
- •3.3. Метод прогонки.
- •3.4 Пример выполнения лабораторной работы №3
- •Вводим функцию, реализующую алгоритм прогонки
- •3.5 Варианты заданий к лабораторной работе №3
- •4 Итерационные методы решения систем линейных алгебраических уравнений
- •4.1. Итерационные методы Якоби и Зейделя.
- •4.2. Каноническая форма итерационных методов.
- •4.3. Вариационно-итерационные методы решения слау.
- •4.4 Пример выполнения лабораторной работы №4
- •Задаем матрицу коэффициентов и столбец свободных членов
- •Вводим функцию, реализующую алгоритм метода Зейделя
- •4.5 Варианты заданий к лабораторной работе №4
- •5 Методы решения задачи Коши
- •5.1. Метод Эйлера.
- •5.2. Метод Рунге-Кутта.
- •Пример выполнения лабораторной работы №5
- •5.4 Варианты заданий к лабораторной работе №5
- •6 Методы приближения функций
- •6.1. Интерполяционный полином Лагранжа и Ньютона.
- •6.2 Интерполяционный кубический сплайн.
- •6.3 Понятие о методе наименьших квадратов.
- •6.4 Интерполяционный тригонометрический полином
- •6.5 Пример выполнения лабораторной работы №6
- •Интерполяционный полином Лагранжа.
- •6.6 Варианты заданий к лабораторной работе №6
3.2. Алгоритм lu-разложения.
Данный алгоритм можно рассматривать как конкретную форму метода Гаусса. Алгоритм LU-разложения используется не только для решения СЛАУ, но и также для обращения матрицы, т.е. вычисления матрицы, обратной данной.
Пусть
 и будем искать представление A
в виде:
и будем искать представление A
в виде:
|
|
(3.10) |
где L и U – соответственно нижняя и верхняя треугольные матрицы вида
 .
.
Известно, что если все угловые миноры матрицы А отличны от нуля, т.е.

то разложение вида (3.10) существует и единственно. Для того чтобы получить расчётные формулы, поступим следующим образом. Обозначим aij произведение i-ой строки матрицы L на j-ый столбец матрицы R, причём будем считать вначале , что i<j.
Тогда
![]() .
.
Выразим из последней формулы uij.
|
|
(3.11) |
Как
это принято, будем считать в формуле
(3.11) и далее, что сумма вида
![]() равна нулю, если значение верхней границы
индекса суммирования меньше нижней
границы.
равна нулю, если значение верхней границы
индекса суммирования меньше нижней
границы.
В случае i = j имеем
![]()
Учитывая, что uii 1 и, выражая из последнего соотношения ii, получаем:
|
|
(3.12) |
Наконец, при i > j получаем
![]()
откуда, с учетом того, что ujj 1 приходим к формуле
|
|
(3.13) |
Итак, расчетные формулы (3.11) – (3.13) получены. Для того чтобы при их применении не использовались неизвестные (не вычисленные) величины, необходимо выбрать соответствующий порядок вычисления элементов матриц L и U.
Например, можно рекомендовать порядок расчета элементов матриц L и U, схематически изображенный на рис. 3.1. На нем цифры слева для матрицы L и сверху - для матрицы U означают, что на первом шаге рассчитывается 11 по формуле (3.12), затем вычисляется элемент u12 по формуле (3.11).
Далее (3 шаг) определяются элементы второй строки матрицы L в порядке, указанном стрелкой: 21 и 22 (по формулам (3.13) и (3.12) соответственно).
На 4 шаге выполняется расчет элементов 3 столбца матрицы U в порядке, обозначенном стрелкой: u13, u23 (формулы (3.11)) и т.д.

Рис. 3.1.
Рассмотрим теперь применение LU-разложения для решения СЛАУ вида
Ах = b,
где
A = LU.
Введем вспомогательный вектор у,
|
у = U x. |
(3.14) |
Тогда исходную систему можно записать так
|
L Ux = b Ly = b. |
(3.15) |
В силу формул (3.14) и (3.15) решение исходной СЛАУ сводится к последовательному решению систем (3.15) и (3.14) соответственно с верхней и нижней треугольной матрицами.
3.3. Метод прогонки.
Метод прогонки представляет собой вариант метода Гаусса, примененный к специальным системам линейных алгебраических уравнений, и учитывающий ленточную структуру матрицы системы. Пусть имеем СЛАУ со специальной трехдиагональной формой матрицы
|
c0y0 – b0y1 = f0, -aiyi-1 + ciyi – biyi+1 = fi, 1 i N-1; -aNyN-1 + cNyN = fN, |
(3.16) |
или в матричной форме: AY = F, где Y = (y0, y1, ..., yn)T - вектор неизвестных; F = (f0,f1,...,fn)T - вектор правых частей; А - квадратная (N+1)(N+1) матрица

Системы вида (3.16) возникают при конечно-разностной аппроксимации краевых задач математической физики, описываемых обыкновенными дифференциальными уравнениями второго порядка с постоянными и переменными коэффициентами, а также уравнениями в частных производных. Ставится задача разработать экономичные методы решения задач вида (3.16), число арифметических операций для которых пропорционально числу неизвестных. Таким методом для системы (3.16) является метод прогонки. Специфика матрицы А состоит в расположении ненулевых элементов, матрица А - разреженная матрица, из (N+1)2 элементов которой ненулевыми являются не более 3N+1 элементов. Это позволяет получить для решения СЛАУ простые расчетные формулы.
Будем искать решение (3.16) в виде
|
yi = i+1yi+1 + i+1, i = N-1, N-2, ..., 0 |
(3.17) |
c неопределенными коэффициентами i, i. Выражение yi-1 = iyi + i подставим в (3.16)
(сi - aii)yi - biyi+1 = fi +aii
c учетом (3.17) имеем
[(сi - aii)i+1 - bi]yi+1 + (ci - aii)i+1 - aii = fi .
Это равенство имеет место для любых yi, если
(сi - aii)i+1 - bi = 0, (сi - aii)i+1 - aii = fi .
Отсюда получаем рекуррентные формулы для определения i+1, i+1
|
|
(3.18) |
|
|
(3.19) |
Коэффициенты i, i, i = 1, 2, ..., N называются прогоночными.
Если коэффициенты i и i известны, а также известно yN то, двигаясь справа налево (от i+1 к i) последовательно определяем все yi. Задача нахождения i, i по формулам (3.18), (3.19) решается слева направо (от i к i+1). Начальные значения прогоночных коэффициентов i, i можно определить следующим образом. Полагаем в формуле (3.17) i=0, имеем y0=1y1+1, а из первого уравнения (3.16) c0y0 - b0y1 = f0, откуда
|
|
(3.20) |
Значение yN определяется следующим образом. Полагаем в формуле (3.17) i=N-1, имеем yN-1 = NyN + N, а из последнего уравнения (3.18) -aNyN-1 + cNyN = fN откуда
|
|
(3.21) |
Расчетные формулы (3.17) - (3.21) можно получить также из (3.16), если применить метод исключения Гаусса. Прямой ход метода заключается в том, что на первом шаге из всех уравнений системы (3.16) при помощи первого уравнения исключается y0, затем из преобразованных уравнений для i=2, ..., N при помощи уравнения, соответствующего i=1, исключается yi и т.д. В результате получим одно уравнение относительно yN. На этом прямой ход метода прогонки заканчивается. На обратном ходе для i=N-1, N-2, ..., 0 находятся yi.
Порядок счета в методе прогонки следующий:
-
исходя из значений 1, 1, вычисленных по формулам (3.20), все остальные коэффициенты i, i для i=2, 3, ..., N-1 определяются последовательно по формулам (3.18) и (3.19);
-
исходя из значения yN, рассчитанного по формуле (3.21), все остальные неизвестные yi, i=N -1, N-2, ..., 0 определяются последовательно по формуле (3.17).
Изложенный метод поэтому называется правой прогонкой.
Аналогично выводятся формулы левой прогонки:
|
|
(3.22) |
|
|
(3.23) |
|
yi+1 = i+1yi + i+1, i = N-1, N-2, …, 0; y0 = 0. |
(3.24) |
Здесь yi находятся последовательно для значений i=1, 2, ..., N; ход вычислений - слева направо.
В случае, если необходимо найти только одно неизвестное, например, ym (0 m N) или группу идущих подряд неизвестных, целесообразно комбинировать правую и левую прогонки. При этом получается метод встречных прогонок.
Произведем подсчет числа арифметических действий для метода правой прогонки. Анализ формул (3.17)-(3.21) показывает, что общее число арифметических операций есть Q=8N+1. Коэффициенты i не зависят от правой части СЛАУ (3.16) и определяются только элементами ai, bi, ci матрицы А. Поэтому, если требуется решить серию задач (3.16) с различными правыми частями, то прогоночные коэффициенты i вычисляются только для первой серии. Для каждой последующей серии задач определяются только коэффициенты i и решение yi, причем используются ранее найденные i.
На решение первой из серии задач расходуется 8N+1 операций, а на решение каждой следующей задачи 5N+3 операций. Число арифметических операций, необходимое для решения СЛАУ (3.16) методом левой прогонки и методом встречных прогонок такое же, т.е. Q8N. Метод правой прогонки будем называть корректным, если ci-aii 0 при i=1,2,...,N.
Решение
yi
находится по рекуррентной формуле
(3.17). Эта формула может порождать
накопление ошибок округления результатов
арифметических операций. Пусть прогоночные
коэффициенты i
и i
найдены точно, а при вычислении yN
допущена ошибка yN,
т.е.
![]() .
При вычислениях с помощью формулы (3.17)
мы получаем
.
При вычислениях с помощью формулы (3.17)
мы получаем
|
|
(3.25) |
Вычитая
из (3.25) значение yi
по формуле (3.17) имеем для погрешности
![]() с заданным yN.
Отсюда ясно, что если i
по модулю больше единицы, и если N
достаточно велико, то вычисленное
значение
с заданным yN.
Отсюда ясно, что если i
по модулю больше единицы, и если N
достаточно велико, то вычисленное
значение
![]() будет значительно отличаться от искомого
решения yi.
В этом случае говорят, что алгоритм
прогонки неустойчив.
будет значительно отличаться от искомого
решения yi.
В этом случае говорят, что алгоритм
прогонки неустойчив.
Определение. Алгоритм прогонки называется устойчивым, если |i| 1, i = 1, 2, …, N.
Условия корректности и устойчивости алгоритма правой прогонки определяются следующей теоремой.
Теорема. Пусть коэффициенты системы (3.16) действительны и удовлетворяют условиям:
|b0| 0, |aN| 0, |c0| > 0, |cN| > 0, |ai| > 0, |bi| 0, i = 1, 2, …, N-1;
|
|ci| |ai| + |bi|, i = 1, 2, …, N-1; |
(3.26) |
|
|c0| |b0|, |cN| |aN| |
(3.27) |
причем хотя бы в одном из неравенств (3.26) и (3.27) выполняется строгое неравенство, т.е. матрица А имеет диагональное преобладание. Тогда для алгоритма (3.17)-(3.21) имеют место неравенства: ci - aii 0, |i| 1, i = 1, 2, …, N, т.е. алгоритм метода правой прогонки корректен и устойчив.
Условия (3.26) и (3.27) теоремы обеспечивают также корректность и устойчивость алгоритмов левой и встречных прогонок. Эти условия сохраняются и для случая системы (3.16) с комплексными коэффициентами ai, bi, ci.
Легко показать, что при выполнении условий (3.26)-(3.27) теоремы система (3.16) имеет единственное решение при любой правой части.

 .
.