
- •Таганрогский государственный радиотехнический университет
- •Введение
- •1 Численное интегрирование
- •1.1 Основные методы численного интегрирования
- •1.2 Пример выполнения лабораторной работы №1
- •1.3 Варианты заданий к лабораторной работе №1
- •2 Методы решения нелинейных уравнений
- •2.1 Метод половинного деления
- •2.2 Метод хорд (метод линейной интерполяции)
- •2.3 Метод секущих
- •2.4 Метод Ньютона
- •2.5 Пример выполнения лабораторной работы №2
- •2.6 Варианты заданий к лабораторной работе №2
- •3 Прямые методы решения систем линейных алгебраических уравнений
- •3.1 Метод Гаусса для решения систем линейных алгебраических уравнений.
- •3.2. Алгоритм lu-разложения.
- •3.3. Метод прогонки.
- •3.4 Пример выполнения лабораторной работы №3
- •Вводим функцию, реализующую алгоритм прогонки
- •3.5 Варианты заданий к лабораторной работе №3
- •4 Итерационные методы решения систем линейных алгебраических уравнений
- •4.1. Итерационные методы Якоби и Зейделя.
- •4.2. Каноническая форма итерационных методов.
- •4.3. Вариационно-итерационные методы решения слау.
- •4.4 Пример выполнения лабораторной работы №4
- •Задаем матрицу коэффициентов и столбец свободных членов
- •Вводим функцию, реализующую алгоритм метода Зейделя
- •4.5 Варианты заданий к лабораторной работе №4
- •5 Методы решения задачи Коши
- •5.1. Метод Эйлера.
- •5.2. Метод Рунге-Кутта.
- •Пример выполнения лабораторной работы №5
- •5.4 Варианты заданий к лабораторной работе №5
- •6 Методы приближения функций
- •6.1. Интерполяционный полином Лагранжа и Ньютона.
- •6.2 Интерполяционный кубический сплайн.
- •6.3 Понятие о методе наименьших квадратов.
- •6.4 Интерполяционный тригонометрический полином
- •6.5 Пример выполнения лабораторной работы №6
- •Интерполяционный полином Лагранжа.
- •6.6 Варианты заданий к лабораторной работе №6
2.6 Варианты заданий к лабораторной работе №2
Найдите корни уравнения используя методы решения нелинейных уравнений.
1.
![]() 6.
6.
![]()
2.
![]() 7.
7.
![]()
3.
![]() 8.
8.
![]()
4.
 9.
9.
![]()
5.
![]() 10.
10.
![]()
Содержание отчета
Отчет должен содержать:
-
титульный лист;
-
постановку задачи (согласно варианту);
-
краткое описание методов расчета нелинейных уравнений;
-
программную реализацию данных методов;
-
выводы о проделанной работе.
Контрольные вопросы и задания
-
Какие методы решения нелинейных уравнений вы знаете?
-
Какой из методов решения нелинейных уравнений, в вашем случае, оказался наиболее быстрым и медленным?
-
Дайте описание метода половинного деления.
-
Запишите расчетную формулу метода хорд.
-
Запишите расчетную формулу метода секущих.
-
Запишите расчетную формулу метода Ньютона.
-
Сформулируйте теорему Больцано–Коши.
-
Решите нелинейное уравнение.
-
Запишите формулу для расчета погрешности метода половинного деления.
-
Запишите формулу для расчета погрешности метода Ньютона.
3 Прямые методы решения систем линейных алгебраических уравнений
Прямые методы теоретически позволяют за конечное число операций (действий) найти «точное» решение системы. Однако, в условиях вычислений на компьютерах, имеющих конечную разрядную сетку, прямые методы позволяют найти реально лишь приближенное решение системы, ввиду наличия погрешностей округления. Примерами прямых методов, рассматриваемых ниже, являются метод Гаусса и его модификации.
3.1 Метод Гаусса для решения систем линейных алгебраических уравнений.
Рассмотрим систему линейных алгебраических уравнений
|
Ах = b , |
(3.1) |
где х = (х1, х2, … хn)Т – вектор неизвестных;
b = (b1, b2, … bn)Т – вектор свободных членов;
А
=
![]() ,
i,j = 1,2,…,n – невырожденная матрица
размерами n
n.
,
i,j = 1,2,…,n – невырожденная матрица
размерами n
n.
В силу невырожденности матрицы А (det A 0) для однородной системы уравнений с вектором правых частей b = (0, 0,…,0)T имеем единственное тривиальное решение х=(0,0,…,0)T. Для неоднородной системы имеем единственное решение х = А-1b, где А-1 – матрица, обратная А.
Алгоритм метода исключения неизвестных был изобретен в 3 веке до нашей эры, хотя и носит имя Гаусса. Идея алгоритма состоит в приведении СЛАУ к эквивалентной ей системе с треугольной матрицей (прямой ход исключения), а затем к нахождению неизвестных последовательными подстановками (обратный ход). Данный метод требует числа арифметических операций порядка 2/3 n3. Он используется для решения СЛАУ с n 102-104.
Объединим матрицу А и вектор b в расширенную матрицу.

размерами n (n+1), которая содержит всю известную информацию о системе (3.1).
Опишем вначале прямой ход, первый шаг которого состоит в обнулении всех элементов первого столбца матрицы А(0), кроме того, что находится в первой строке.
Введем обозначение
аi = (ai1, ai2, … ain, bi).
C матрицей А(0) можно обращаться так же, как с исходной системой (3.1), например, осуществлять элементарные преобразования. В качестве последних будем использовать перестановки строк, прибавление к элементам данной строки элементов какой-либо другой строки, умноженных на одно и то же число.
Найдем ненулевой элемент в первом столбце матрицы А(0). Такой элемент найдется всегда ибо, в противном случае, весь первый столбец состоит из нулей и матрица А – вырожденная. Пусть аr1 0, тогда поменяем местами строки номера r и 1. Если r = 1, то, естественно, перестановка не требуется. Затем вычтем из каждой строки номера i, i = 2, … , n первую строку, умноженную на число fi, где
![]() .
.
В результате все элементы i-ой строки изменят свои значения и станут равными
|
|
(3.2) |
Здесь мы предполагаем, что хотя перестановка строк и могла состояться, однако нумерация элементов матрицы А(0) осталась прежней. Введем обозначения
|
|
(3.3) |
С учетом введенных обозначений (3.2) и (3.3) матрица А(0) преобразуется к матрице А(1) и станет равной
|
|
(3.4) |
Тот же алгоритм может быть применен на втором шаге к (n-1) n матрице, которая получается из А(1), если убрать в ней первую строку и первый столбец. Применение этого алгоритма j раз приводит к матрице А(j)

В матрице А(j) полученные нули располагаются в столбцах с номерами от 1 до j ниже диагонали. Эти нули сохраняются во время следующих шагов алгоритма. В результате применения алгоритма n раз система (3.1), в конечном счете, преобразуется в систему вида
|
R x = C |
(3.5) |
где R – верхняя (правая) треугольная матрица, т.е.
|
|
(3.6) |
Значения неизвестных можно вычислить из (3.6) по формулам
|
xn = cn / rnn,
|
(3.7) |
Процесс приведения системы (3.1) к треугольному виду (3.6) называется прямым ходом, а нахождение неизвестных по формулам (3.7) называется обратным ходом.
Произведем подсчет числа арифметических операций в методе Гаусса. Число арифметических операций, необходимое для реализации прямого хода в методе Гаусса для решения систем уравнений порядка n, равно
|
|
(3.8) |
При обратном ходе
|
QII = n(n – 1) = n2 – n. |
(3.9) |
Из формул (3.8) и (3.9) получаем оценку общего числа арифметических действий
![]() .
.
Если
имеется р систем вида (3.1) с одинаковыми
матрицами А и разными правыми частями
![]() ,то
целесообразно прямой ход осуществлять
для всех систем одновременно, для чего
следует вместо одной правой части,
задаваемой вектором-столбцом, производить
операции над р правыми частями (матрицей
порядка np).
Количество арифметических операций,
необходимое для реализации прямого
метода Гаусса с учетом (3.8) и (3.9), есть
,то
целесообразно прямой ход осуществлять
для всех систем одновременно, для чего
следует вместо одной правой части,
задаваемой вектором-столбцом, производить
операции над р правыми частями (матрицей
порядка np).
Количество арифметических операций,
необходимое для реализации прямого
метода Гаусса с учетом (3.8) и (3.9), есть
![]() .
.
Количество арифметических операций, необходимое для реализации р обратных ходов (для р систем) методом Гаусса, есть QIIp= p(n2 – n). Откуда следует, что общее количество арифметических операций, необходимое для реализации р систем с разными правыми частями, равно
![]() .
.


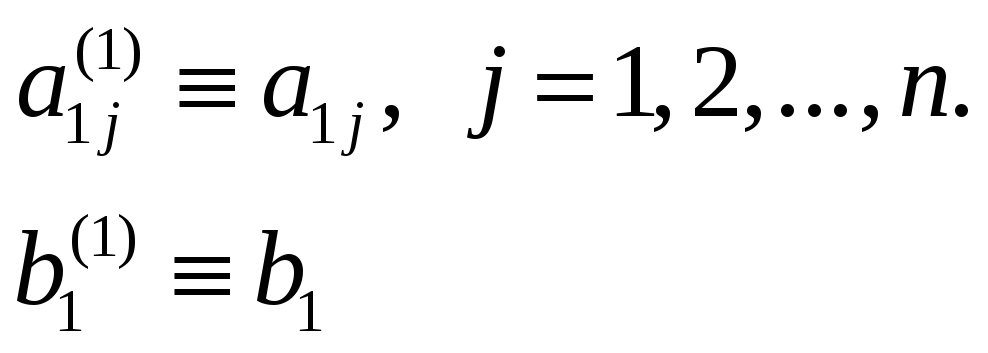
 .
. .
. .
.