Кинематика

Задача К1

Кинематика точки

Возьмем вариант 77, согласно которому должны использоваться данные рис. К1.7 и таблицы К1.1 –7-й столбец [1], в которых заданы уравнения движения точки в декартовых координатах в виде х=4соs²(t/6); у = 5sin(t/6),см.

По тексту условия задачи указано, что в момент t=2с движущаяся точка М достигает точки Д и далее движется по окружности радиуса R=5см с ускорением а_= 2t₁–1 см/с² в течение t₁ = 3с до точки Е.

Требуется определить: для 1-го участка – уравнение траектории, скорость, ускорение и радиус кривизны траектории в точке Д; для 2-го участка – положение точки Е, ее скорость, касательное и нормальное ускорения. Кроме этого, необходимо построить графически оба участка траектории и показать все полученные величины.

Таким образом, задано: х=4соs²(t/6), у = 5sin(t/6)см, t=2с; R=5см, а_= 2t₁–1,см/с², t₁ = 3с;

определить: у=f(x), ρ_Д, V_Д, а_Д; φ_Е, V_Е, , .

Решение

Возведем второе уравнение движения в квадрат и получим

х/4=соs²(t/6);

(у/5)²=sin²(t/6).

После сложения уравнений имеем уравнение траектории в виде

,

которое показывает, что это парабола

. (1)

В момент времени t=2с точка занимает положение, определяемое координатами:

х=4соs²(t/6)=4соs²(2/6)=4соs²60⁰=4·0,25=1см;

у=5sin(t/6)=5sin(2/6)=5·0,866=4,33см.

При t=0 координаты точки составляли:

х=4соs²0=4см; у=5sin0см=0.

Проекции скорости точки:

при t=2c→ V_x= –(4/3)sin(2/3)= –(4/3)sin120⁰= –3,6275см/с.

при t=2c→ V_у=(5/6)соs(2/6)=(5/6)соs60⁰=1,309см/с.

Следовательно,

V_Д=3,856см/с.

Проекции ускорения точки:

;

при t=2c→ а_х= –(4π²/9)соs(2π/3)= –(4π²/9)соs(120⁰)=2,193cм/c².

при t=2c→ а_у= –(5π²/36)sin(2π/3)= –(5π²/36)sin120⁰= –1,187cм/c².

Тогда

а_Д==2,493см/с².

Далее

а_τ=(V_xа_x+V_yа_y)/V=[(–3,6275)(2,193) + (1,309)(–1,187)]/3,856= –2,466см/с².

а_n==0,366см/с².

Следовательно,

ρ=V_Д²/а_n=3,856²/0,366=40,625см.

П редставим полученные данные на рис К1а.

Дальнейшее движение по окружности:

=.

При t₁=0→ V_Д=C₁=3,865см/с, поэтому

.

В момент времени t₁=3c скорость в точке Е будет

V_E=3² –3 +3,865=9,865см/с.

Следовательно, для точки Е

а_n=V²/R=9,865²/5=19,464cм/с²;

а_= 2t₁–1=2·3-1=5см/с².

Положение точки Е

s=.

Так как для точки Д→ s=0, следовательно, С₂=0, а

s_Е=3³/3-3²/2+3,865·3=16,095см,

что соответствует углу

φ=s/R=16,095/5=3,219рад=3,219·180/π=184,4⁰

как и представлено на рис К1а.

Задача К2

Возьмем трехзначный вариант 729, согласно которому схема должна быть по рис. К2.7, основные данные – из табл. К2.1 (столбец 2), дополнительные данные – из табл. К2.2 (столбец 9).

Из текста условия следует, что радиусы ступеней колес составляют: r₁=4, R₁=10, r₂=5, R₂=12, r₃=8, R₃=16см, а расчетный момент времени t = 2с.

В табл. К2.1 задан закон изменения =3t²-2t с^-1, при этом положительное направление отсчета – против хода часовой стрелки.

По таблице К2.2 для заданного момента времени требуется определить: скорость груза 4 V₄, угловую скорость блока 1 ₁, угловое ускорение блока 3 ₃, ускорение точки С блока 1 а_С, количество оборотов блока 2 z₂ за заданное время.

Таким образом, задано: =3t²-2t, с^-1; r₁=4, R₁=10, r₂=5, R₂=12, r₃=8, R₃=16см; t = 2с;

определить: V₄, ₁, ₃, а_С, z₂.

Решение

Прежде всего, определим угловое ускорение блока 3.

с^-2.

Следовательно, при t =2с

₃=6·2–2=10с^-2.

Используем заданную схему, приведенную на рис. К2а, в качестве расчетной.

В момент времени t = 2с угло-вая скорость

₃=3t²-2t=3·2²-2·2=8с^-1.

С учетом этого

V₄=₃r₃=8·8=64см/с.

Используя передаточные отношения, получим

,

следовательно,

(3t²-2t)16/5=3,2(3t²–2t)с^-1.

При t =2с

₂=3,2(3t²–2t)=3,2(3·2²–2·2) =25,6с^-1;

при t =0→ ₂=0.

Однако угловая скорость ₂ становится равной нулю еще в один момент времени, а именно

3,2(3t²-2t)=0 → t=2/3=0,667с.

Это означает, что механизм движется сначала в одну сторону, а затем – в другую. Поэтому определим углы поворота.

=3,2(t³–t²) +С₁.

Так как отсчет угла предусмотрен от нулевого положения, то С₁=0 и угол φ₂ соответственно равен

t=0,667с→ φ₂₁=3,2(t³–t²)=3,2(0,667³–0,667²)= –0,474рад;

t=2с→ φ₂₂=3,2(2³-2²)=12,8рад.

Тогда общее количество оборотов шестерни 2 в ту и другую стороны составит

z₂=2(|φ₂₁|/2π) +(φ₂₂/2π) = 2(0,447/2π)+(12,8/2π)=2(0,071)+2,037= 2,179об.

Так как заданная точка С принадлежит блоку 1, необходимо определить его угловую скорость и угловое ускорение. Используя передаточные отношения, получим:

₁=₂(R₂/r₁)=₃(R₂R₃/r₁r₂)=8(12·16/4·5)=76,8с^-1;

₁=₂(R₂/r₁)=₃(R₂R₃/r₁r₂)=10(12·16/4·5)=96с^-2.

Тогда

а_Сⁿ=₁²R₁=76,8²·10=58982,4см/с²=589,8м/с²;

а_С^τ=₁R₁=96·10=960см/с²=9,6м/с²;

а_С==589,9м/с².

Все полученные величины представлены на рис. К2а.

Задача К3

Плоскопараллельное движение твердого тела

Возьмем двузначный вариант 49, для которого схема должна быть по рис. К3.4, а данные – по таблице К3.1 столбец 9.

По тексту условия заданы: угловая скорость и угловое ускорение звена 1 ₁ = 4с^-1, ₁ = 10 с^-2; размеры звеньев механизма l₁ = 0,4м, l₂ = 4l₁, l₄ = 5l₁, l₅ =2l₁, r₃ = 0,2м, R₃ = 1,5r₃, R = 3R₃; углы  = 60⁰, ₃ = 120⁰.

Из таблицы К3.1 следует: ₁=0, ₂=60⁰, =150⁰.

Исходная схема с учетом этих данных представлена на рис. К3а, при этом АД=ДВ.

Требуется определить скорости точек А, К, Е; угловые скорости звеньев ₂, ₃, ₄; ускорение точки В и угловое ускорение ₂, т.е. звена 2.

Таким образом, задано: ₁ = 4с^-1, ₁ = 10 с^-2, l₁ = 0,4, l₂ = 1,6, l₄ = 2,0, l₅= 0,8м, r₃ = 0,2, R₃ = 0,3, R = 0,9м; ₁=0, ₂=60⁰, ₃ = 120⁰, =150⁰,  = 60⁰; АД= ДВ=0,8м;

определить и построить: , ₂, ₃, ₄, , ₂.

Решение

Воспользуемся схемой, представленной на рис К3а и построим векторы скоростей точек А, В, Д, Е, К, мгновенные центры скоростей Р₂ и Р₃ и покажем угловые скорости ₂, и ₃. Мгновенный центр скоростей звена 4 уходит в бесконечность, поэтому ₄= 0. Кроме этого, АД=ДВ=АР₂, поэтому треугольник АДР₂ равностопронний.

Скорость точки А:

V_A=₁О₁А=₁l₁=4·0,4=1,6м/с.

Так как АP₂=ДP₂, то

V_Д=V_A=1,6м/с.

По теореме о проекциях скоростей (на прямую АВ) получим

V_Вcos60⁰=V_Acos30⁰→ V_В=V_Atg60⁰=1,6tg60⁰=2,771м/с.

Скорости V_Д и V_Е оказались параллельными, поэтому

V_Е = V_Д=1,6м/с.

Угловыю скорости ₂ и ₃ найдем по формулам:

₂ =V_A/АР₂ = V_A/0,5l₂= 1,6/(0,5·1,6)= 2с^-1;

₃ =V_В/ВР₃ =V_В/R₃ = 2,771/0,3=9,237с^-1.

Тогда

V_К=₃·КР₃==3,33м/с.

Для определения ускорений воспользуемся схемой, представленной на рис. К3б.

Прежде всего, представим ускорение точки В в виде векторной формулы, учитывая, что точка В движется по окружности радиуса R+R₃, т.е.

. (1)

Определим составляющие, входящие в это выражение.

а_Аⁿ=ω₁²О₁А=ω₁²l₁=4²·0,4=6,4м/с².

а_А^τ=ε₁О₁А=ε₁l₁=4·0,4=1,6м/с².

=2²·1,6=6,4м/с².

=6,39м/с².

Остальные составляющие пока остаются неизвестными, поэтому построим многоугольник ускорений точки В согласно выражения (1). Если выдержать масштаб для векторов ускорений, то получим графическое решение задачи. Штриховые линии на рис. К3б показывают, как следовало направлять заранее неизвестные ускорения при построении многоугольника.

Проведем из точки В оси координат «х,у», чтобы одна из осей была направлена вдоль АВ и спро-ектируем на них выра-жение (1).

а_Вх= –а_Аⁿcos30⁰+а_А^τsin30⁰+а_BA^τ=а_Bⁿsin30⁰+а_B^τcos30⁰. (2)

а_Ву=а_Аⁿcos60⁰+а_А^τsin60⁰–а_BAⁿ=а_Bⁿsin60⁰–а_B^τcos60⁰. (3)

Из выражения (3) получим

=

=0,5(–6,4cos30⁰–1,6sin30⁰+6,4+6,39sin60⁰)=2,796м/с².

Следовательно,

=6,975м/с².

Из выражения (2) найдем, что

а_BA^τ=а_Аⁿcos30⁰–а_А^τsin30⁰+а_Bⁿsin30⁰+а_B^τcos30⁰=

=6,4cos30⁰–1,6sin30⁰+6,39sin30⁰+2,796cos30⁰=10,358м/с².

В свою очередь, это позволяет определить, что

.

Направление всех полученных величин показано на рис. К3б. Если бы какая-либо из них получилась со знаком «минус», то это означало бы, что не выдержан масштаб построения или при решении допущена ошибка.

Задача К4

Сложное движение точки

Возьмем трехзначный вариант 935. Это означает, что схема должна быть по рис К4.9, данные из таблицы К4.1 по строке 3, а дополнительные данные, касающиеся направления движения, – по строке 5 таблицы К4.2.

Из таблицы К4.1 имеем закон изменения угла поворота тела

 = (4t+t²)/3 рад

и закон относительного движения точки по окружности

S = АМ =(2/3)Rcos((1+t/6))см.

Кроме этого, из таблицы К4.2 следует, что угол поворота  должен отсчитываться против хода часовой стрелки, координата S – по ходу, а расчетное время t должно составлять 1с (в отличие от двузначных вариантов, для которых эти параметры заданы по тексту условия и на схемах).

Из условия задачи следует, что радиус кольца трубки R составляет 30см, а требуется определить абсолютную скорость и абсолютное ускорение точки в заданный момент времени.

Таким образом, задано: S =АМ=(2/3)Rcos((1+t/6))см,  = (4t+t²)/3 рад, R=30см, t=1c;

определить: V, а.

Решение

С учетом заданных условий схема по варианту должна выглядеть, как пред–

ставлено на рис. К4а.

Прежде всего, определим положение точки в заданный момент времени, т.е.

S =АМ =(2/3)Rcos((1+t/6))=(2/3)Rcos((7/6))=

=(2/3)Rcos210⁰=см.

Это соответствует углу

рад= –103,9.

Движение точки по вращающемуся кольцу следует считать относительным, а движение вместе с кольцом – переносным. Используем в качестве расчетной схему, представленную на рис. К4б.

Относительное движение

Для момента времени t=1c относительная скорость составит

=16,45см/с.

.

П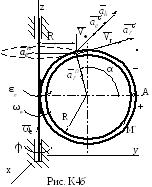ри t=1c относительное касательное ус-корение

14,92см/с².

Для определения относительного нор-мального ускорения используем формулу

9,02см/с².

Переносное движение

Прежде всего определим радиус переносного вращения с учетом положения точки и величины угла α:

R_e=R–Rsin(α–90⁰)=30(1–sin14⁰)=17,24см.

Для определения угловой скорости и углового ускорения продифференцируем угол φ.

=6,28с^-1.

6,28с^-2 = ε_е.

Тогда

V_e=ω_eR_е=6,28·17,24=108,27см/с.

а_еⁿ= ω_e²R_е=6,28² 17,24=679,9см/с².

а_е^τ= ε_еR_е=6,28·17,24=108,27см/с².

Ускорение Кориолиса:

а_к=2ω_eV_rsin(180⁰-α)=2·16,45sin76⁰=31,92см/с².

Абсолютное движение

Так как

,

,

то покажем на схеме все эти составляющие и спроектируем их на оси координат и произведем вычисление.

V_X= –V_e= –108,27см/с.

V_y=V_rcos14⁰=16,45cos14⁰=15,96см/с.

V_z=V_rsin14⁰=16,45sin14⁰=3,00см/с.

Следовательно,

V==109,5см/с =1,10м/с.

а_х = –а_е^τ – а_к= –108,27 – 31,92 = –140,19см/с².

а_у = –а_eⁿ + а_rⁿsin14⁰ +а_r^τcos14⁰= –679,9 +9,02sin14⁰ +14,92cos14⁰ = –663,24см/с².

а_z = –а_rⁿcos14⁰+а_r^τsin14⁰= –9,02cos14⁰+14,92sin14⁰= –5,14см/с².

а===677,9см/с²=6,78м/с².

Таким образом, абсолютная скорость точки невелика, а абсолютное ускорение не превышает величины ускорения свободного падения g.