2.4 Статистический анализ модели многомерной регрессии

2.4.1 Разложение дисперсии

Статистический анализ модели многомерной регрессии проводится аналогично анализу простой линейной регрессии. Стандартные пакеты статистических программ позволяют изучить оценки по методу наименьших квадратов для параметров модели, оценки их стандартных ошибок, а также значение t-статистики, используемой для проверки значимости отдельных слагаемых регрессионной модели, и величину F-статистики, служащей для проверки значимости регрессионной зависимости. Вычисление указанных значений вручную при многомерном регрессионном анализе крайне непрактично - подобные вычисления следует проводить только с помощью компьютера.

является прогнозом, вычисленным по найденному уравнению регрессии.

Форма разбиения суммы квадратов и соответствующие степени свободы здесь следующие:

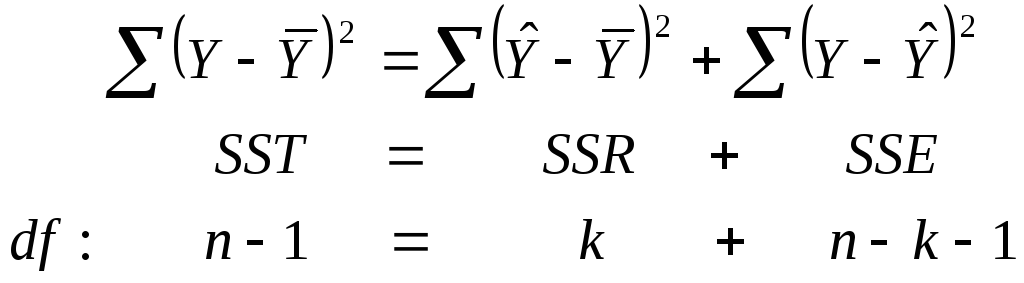
Общая вариация зависимой переменной, SST, состоит из двух компонент: SSR, вариации, объясненной независимыми переменными через функцию регрессии, и SSE, необъясненной вариации. Информация из уравнения может быть получена в таблице анализа дисперсии ANOVA.

2.4.2 Стандартная ошибка дисперсии

Стандартная ошибка оценки – это стандартное отклонение для значений остатков. Она измеряет рассеивание значений переменной Y относительно линии функции регрессии:

где n – количество наблюдений;

k – количество независимых переменных в функции регрессии;

- сумма квадратов остатков;

- среднее квадратов остатков.

Таким образом, стандартная ошибка оценки измеряет отклонение имеющихся данных (Y) от их оценок (). Для сравнительно больших выборок следует ожидать, что около 67% разностей будут иметь абсолютную величину не более чем и около 95% из этих разностей по модулю не будут превосходить 2.

2.4.3 Значимость регрессии

Таблица анализа дисперсии ANOVA строится на разложении общей вариации Y (SST) на объясненную (SSR) и необъясненную (SSE) части. Общий ее вид при­веден в табл. 2.

Таблица 2 - Таблица анализа дисперсии ANOVA

Источник	Сумма квадратов	Степени свободы	Среднеквадратическое значение	Отношение F
Регрессия	SSR	k	MSR=SSR/k	F=MSR/MSE
Ошибки	SSE	n-k-1	MSE=SSE/(n-k-1)
Сумма	SST	n-1

Рассмотрим гипотезу . Справедливость этой гипотезы означает, что величина Y не связана ни с какой из переменных X (коэффициент при каждой переменной X, равен нулю). Проверка гипотезы фактически является проверкой значимости регрессии. Если регрессионная модель справедлива и гипотеза верна, отношение F=MSR/MSE имеет F-распределение с числом степеней свободы df = k, n-k-1. Значит, величину F можно использовать для проверки значимости регрессии.

В простой линейной регрессии имеется лишь одна независимая переменная. Поэтому для нее проверка значимости регрессии, использующая величину отношения F из таблицы ANOVA, эквивалентна двухстороннему t-критерию проверки гипотезы о равенстве нулю углового коэффициента. Для многомерной регрессии t-критерий проверяет значимость каждой отдельной переменной X в функции регрессии, а F-критерий — значимость всех переменных X вместе.

При уровне значимости гипотеза отклоняется, если (расчетное значение F больше значения F-распределения при уровне значимости с числом степеней свободы ).

Коэффициент детерминации вычисляется по формуле:

Коэффициент детерминации имеет такой же вид и такую же интерпретацию, как и для простой линейной регрессии. Он представляет собой долю вариации зависимой переменной Y, которая объясняется взаимосвязью Y с переменными X.

Значение = 1 говорит о том, что наблюдаемые значения Y в точности соответствуют найденной функции регрессии. Вся вариация зависимой переменной объясняется регрессией. Значение = 0 указывает, что , а это означает, что SSR = 0, и никакая часть вариации величины Y не объясняется регрессией. На практике значение обычно лежит в диапазоне 0 < < 1 и интерпретируется в зависимости от его близости к 0 или 1.

Величина называется многомерным коэффициентом корреляции и характеризует корреляцию между зависимой переменной Y и прогнозом. Поскольку прогнозирует значение зависимой переменной, значение R всегда неотрицательно и лежит в диапазоне 0 < R < 1.

Для многомерной регрессии:

поэтому, при прочих равных показателях, значимые регрессионные зависимости соответствуют сравнительно большим значениям .