
- •Декартовий добуток множин.
- •VIII. Зображення декартового добутку множин на координатній площині
- •2 Семестр
- •Про історію виникнення натурального числа.
- •Порядкові і кількісні натуральні числа. Рахунок.
- •Теоретико – множний зміст кількісного числа і нуля.
- •Додавання. Закони додавання.
- •1. Порівняння.
- •Правила віднімання числа з суми і суми із числа:
- •Поняття відношення подільності.
- •Властивості відношення подільності.
- •Подільність суми, різниці і добутку цілих невід‘ємних чисел.
- •Признаки подільності чисел.
- •Найбільший спільний дільник і найменше спільне кратне.
- •Властивості нсд.
- •Властивості нск.
- •Признаки подільності на складові числа.
- •Знаходження нсд і нск чисел способом розкладу на прості множники.
- •Алгоритм Евкліда.
- •II курс
- •I. Поняття функції.
- •Способи завдання функції.
- •Властивості функції.
- •Графік функції.
- •Лінійні функції, їх властивості і графік.
- •Обернена залежність, її властивості.
- •Квадратичні функції, їх властивості.
- •Довжина відрізку і її вимірювання.
- •Площа фігури, способи її вимірювання.
- •Об‘єм тіла, його вимірювання.
- •Маса, вартість, швидкість, час. Одиниці вимірювання.
- •VI. Залежність між величинами.
- •Числовий вираз і його значення.
- •Вираз зі змінною і його область визначення.
- •Тотожні перетворення виразів.
- •Означення рівняння.
- •Рівносильні рівняння.
- •Властивості рівнянь.
- •Числові Нерівності.
- •2. Основні властивості нерівностей.
- •4 Семестр
- •Геометричні фігури.
- •Кути, їх види, побудова.
- •Признак паралельності прямих.
- •Перпендикуляр до прямої.
II курс
Лекція 17. Поняття функції. Графік функції.
Мета: ввести поняття функції однієї змінної, навчити знаходити область визначення функції, задавати функцію, будувати графік функцій. Розглянути лінійну функцію, квадратичну функцію і обернену пропорційність. Розвивати просторове уявлення і пам‘ять студентів.
План:
-
Поняття функції.
-
Способи завдання функції.
-
Властивості функції.
-
Графік функції.
I. Поняття функції.
Функцією
називається така залежність змінної
![]() від змінної
від змінної
![]() ,
при якій кожному значенню
,
при якій кожному значенню
![]() відповідає єдине значення
відповідає єдине значення
![]() .
.
Змінну
![]() називають не залежною
змінною або аргументом, змінну
називають не залежною
змінною або аргументом, змінну
![]() - залежною.
Кажуть також, що
- залежною.
Кажуть також, що
![]() являється функцією від
являється функцією від
![]() .
Значення
.
Значення
![]() ,
яке відповідає заданому значенню
,
яке відповідає заданому значенню
![]() ,
називають значенням функції.
,
називають значенням функції.
-
Способи завдання функції.
Щоб задати функцію, потрібно
задати числову множину
![]() (її називають областю визначення функції)
і спосіб, за допомогою якого для кожного
числа
(її називають областю визначення функції)
і спосіб, за допомогою якого для кожного
числа
![]() з області визначення можна знайти
відповідне число
з області визначення можна знайти
відповідне число
![]() - значення функції. Функцію прийнято
позначати
- значення функції. Функцію прийнято
позначати
![]() .
.
Найчастіше функції задають
за допомогою формул,
які вказують, як по заданому значенню
аргументу знайти відповідне значення
функції. Іноді функцію задають задають
таким чином:
![]() ,
тобто на різних областях значення
аргументу задається різними формулами.
Також існує табличний і графічний
способи завдання функції.
,
тобто на різних областях значення
аргументу задається різними формулами.
Також існує табличний і графічний
способи завдання функції.
-
Властивості функції.
-
монотонність. Функція називається зростаючою на деякому проміжку, якщо для будь-яких
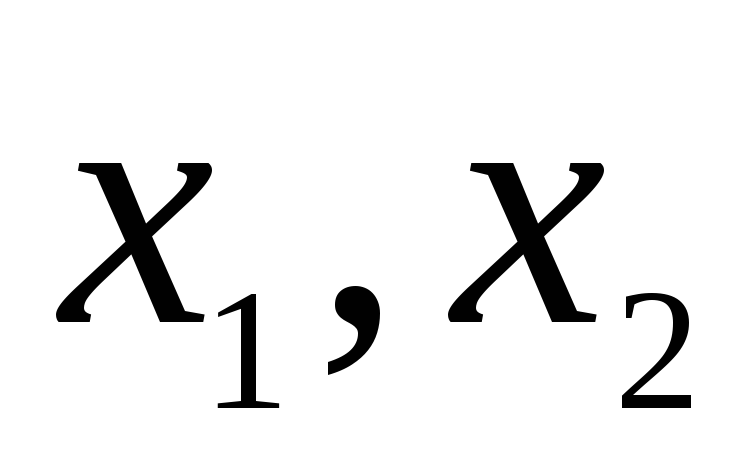 виконується умова
виконується умова
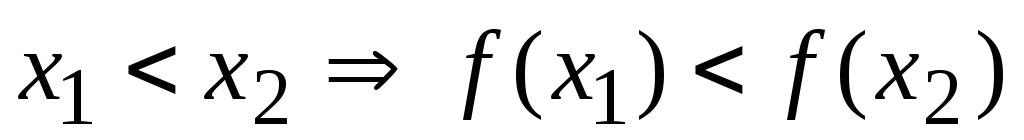 .
Функція називається спадною, якщо для
будь-яких
.
Функція називається спадною, якщо для
будь-яких
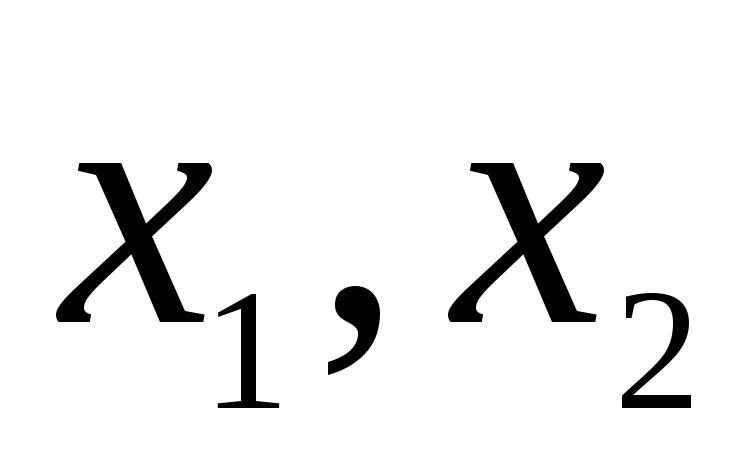 виконується умова
виконується умова
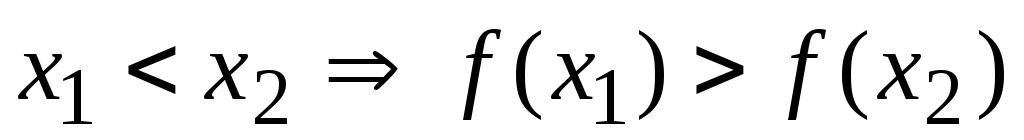 .
. -
парність.
-
перілдичність
-
Графік функції.
Графічне зображення функції не тільки дозволяє уявити функціональну залежність наглядно, але надає можливість спростити вивчення її властивостей. Тому навіть в тому випадку, якщо функція задана аналітично, часто звертаються до її графіку на координатній площині.
Графіком функції
![]() ,
заданої на множині
,
заданої на множині
![]() ,
називається множина таких точок
координатної площини, які мають координати
,
називається множина таких точок
координатної площини, які мають координати
![]() і
і
![]() для всіх значень
для всіх значень
![]() з множини
з множини
![]() .
.
Лекція 18. Лінійні і квадратичні функції, та їх властивості.
Мета: розглянути лінійні і степеневі функцію, їх властивості і побудову графіка. Навчити будувати графіки лінійних та квадратичних функцій за допомогою зміщення вісей координат. Розвивати пам‘ять, логічне мислення, просторове уявлення і охайність студентів.
План:
-
Лінійні функції, їх властивості і графік.
-
Обернена залежність, її властивості.
-
Квадратичні функції, їх властивості.
-
Степенева функція.
-
Лінійні функції, їх властивості і графік.
-
Лінійна залежність між двома
величинами виражається рівністю
![]() ,
де
,
де
![]() - певні числа. При заданих
- певні числа. При заданих
![]() значення
значення
![]() залежить від значення
залежить від значення
![]() ,
значить, можна вважати
,
значить, можна вважати
![]() аргументом,
аргументом,
![]() - функцією. Функція такого виду називається
лінійною. Багаточлен першого степеня
відносно аргументу називається лінійною
функцією цього аргументу.
- функцією. Функція такого виду називається
лінійною. Багаточлен першого степеня
відносно аргументу називається лінійною
функцією цього аргументу.
Теорема. Графіком лінійної функції являється пряма.
Розглянемо деякі частинні
випадки функції
![]() .
.
-
Нехай
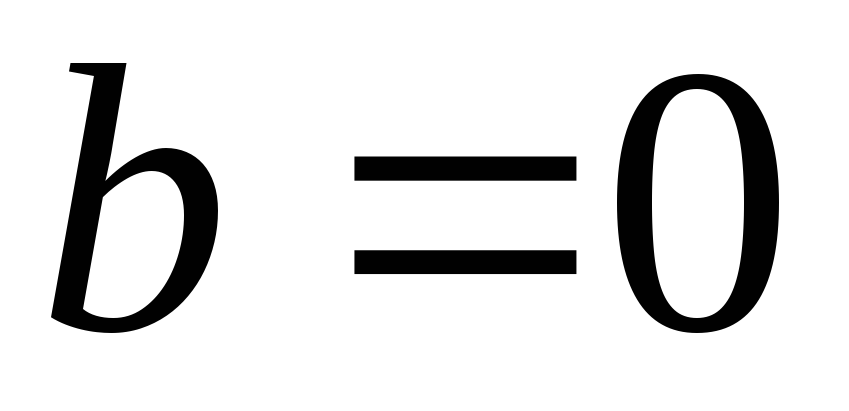 .
Тоді
.
Тоді
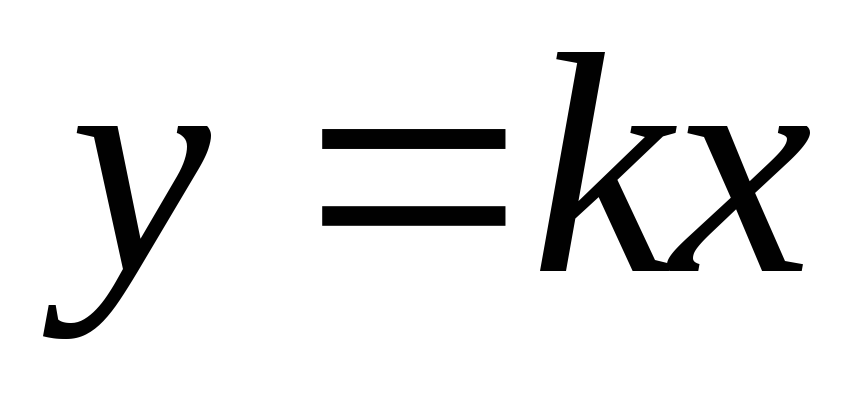 .
Графіком цієї функції являється пряма,
яка проходить через початок координат
.
Графіком цієї функції являється пряма,
яка проходить через початок координат
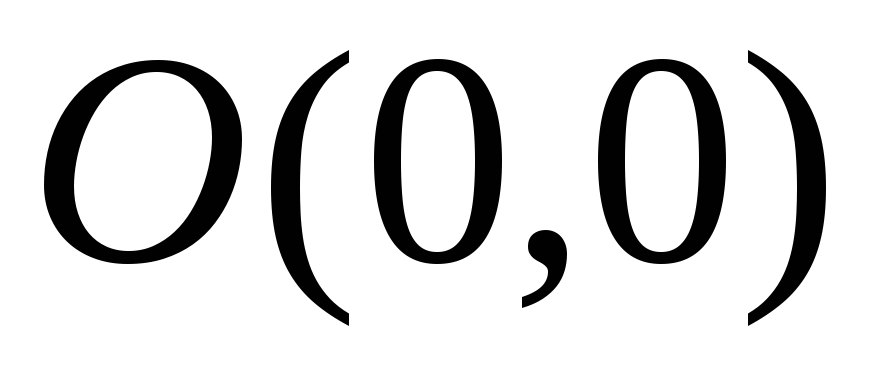 .
. -
Нехай
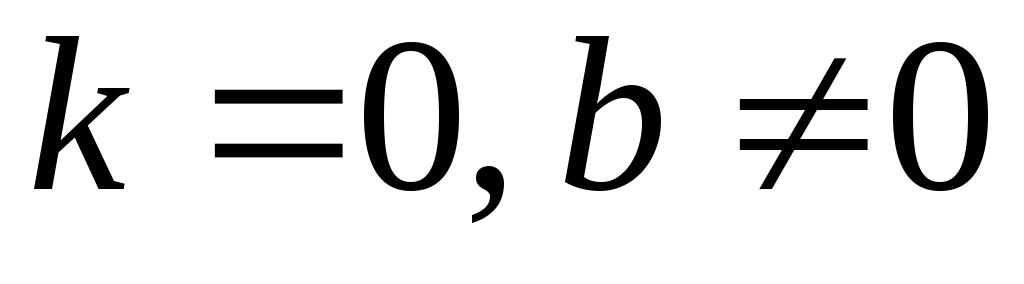 .
Тоді
.
Тоді
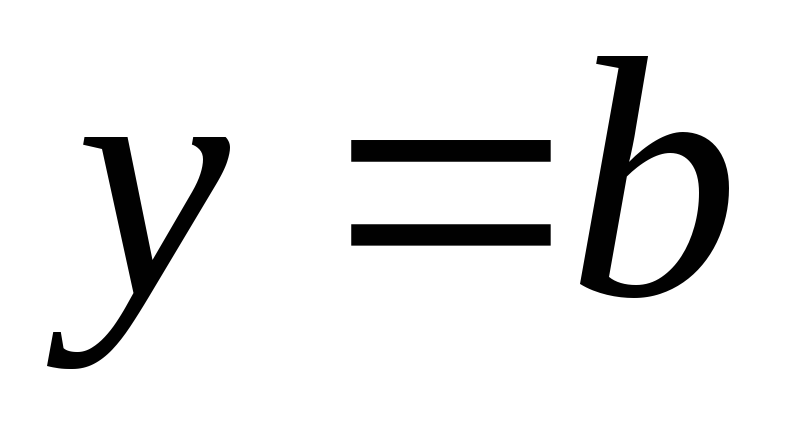 .
З цієї рівності видно, що при будь-якому
значенні
.
З цієї рівності видно, що при будь-якому
значенні
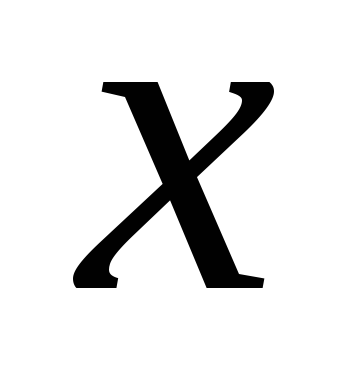 ордината функції буде дорівнювати
ордината функції буде дорівнювати
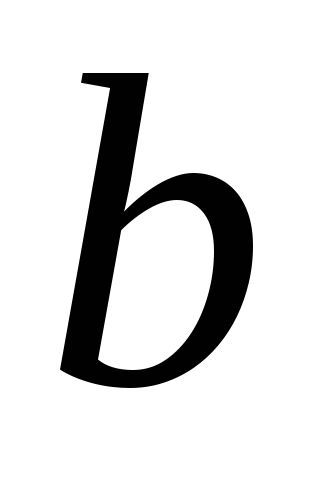 .
Це значить, що всі точки графіка
знаходяться на однаковій відстані
від вісі абсцис. При
.
Це значить, що всі точки графіка
знаходяться на однаковій відстані
від вісі абсцис. При
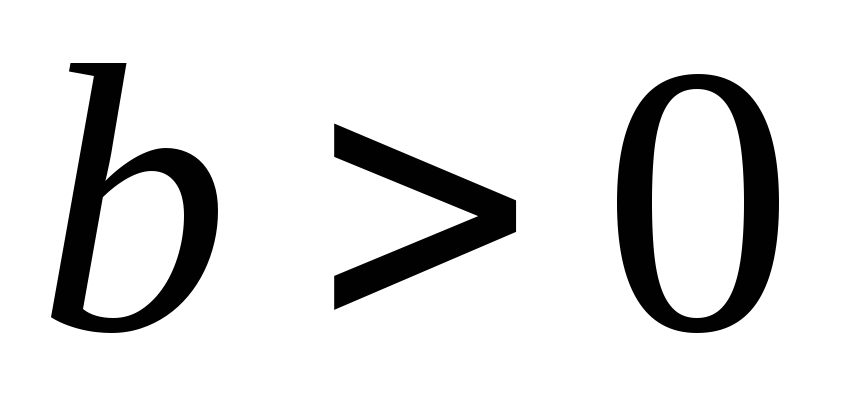 графік лежить вище, при
графік лежить вище, при
 нижче вісі абсцис. Іншими словами,
графіком функції є пряма, паралельна
вісі абсцис.
нижче вісі абсцис. Іншими словами,
графіком функції є пряма, паралельна
вісі абсцис. -
Нехай
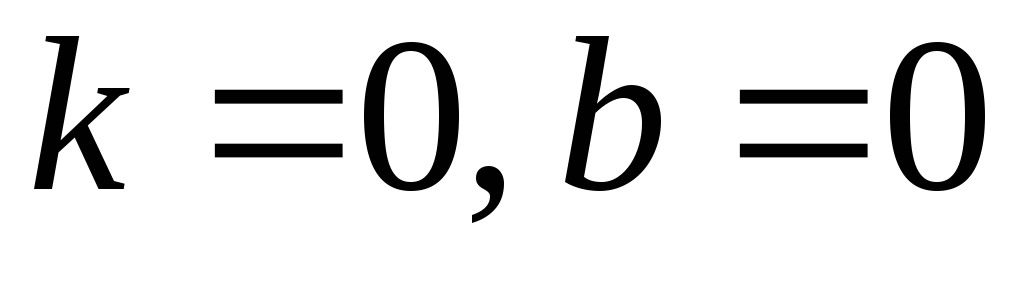 ,
тоді при будь-якому значенні
,
тоді при будь-якому значенні
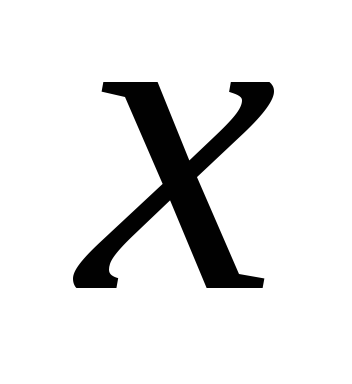 ордината
ордината
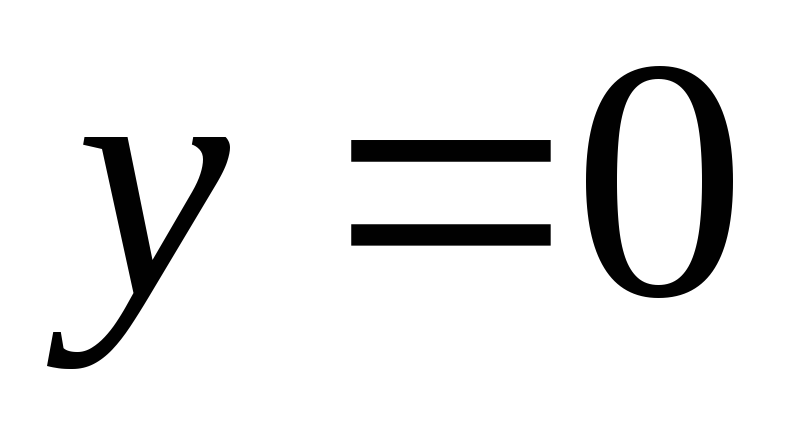 .
Очевидно, що цій умові задовольняють
всі точки вісі абсцис, значить, графіком
функції
.
Очевидно, що цій умові задовольняють
всі точки вісі абсцис, значить, графіком
функції
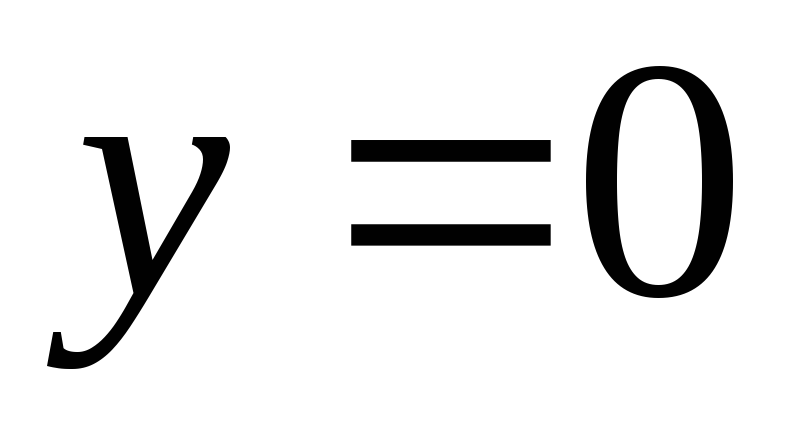 є вісь абсцис.
є вісь абсцис.
