1. Поняття відношення подільності.

Як відомо, віднімання і ділення цнч виконується не завжди. Тому математики з давних давен намагалися відшукати такі правила, які б дозволяли за записом числа дізнатися, ділиться воно на інше число чи ні, не виконуючи безпосереднього ділення цих чисел.

Припустимо задані цнч . Якщо при діленні з залишком числа на залишок дорівнює нулю, то число називається дільником числа . З цього означення випливає, що якщо - дільник числа , то існує таке число , що . Термін «дільник» і «дільник числа» потрібно відрізняти. Наприклад, якщо 18 ділять на 5, то 5 – дільник, але не являється дільником числа 18. В тому випадку, коли число - дільник , то говорять, що кратно , і записують . Множина дільників числа скінчена, наприклад, дільники числа 36 : .

В залежності від кількості дільників натуральні числа розподіляють на прості і складові. Простим числом називається таке натуральне число, яке має тільки два дільника – одиницю. І саме це число. Наприклад, 2,3,5,7,11,13,17, 19,23 …. Складовим числом називається таке натуральне число, яке має більше двох дільників. Наприклад, 4,6,8,… Число 1 не являється ні простим, ні складовим.

Чисел, кратних заданому, можна назвати безліч. Наприклад, числа, кратні 4 – 0, 4, 8, 12, 24, 68,…

2. Властивості відношення подільності.

   1. Кожне натуральне число ділиться само на себе.

   2. для різних чисел 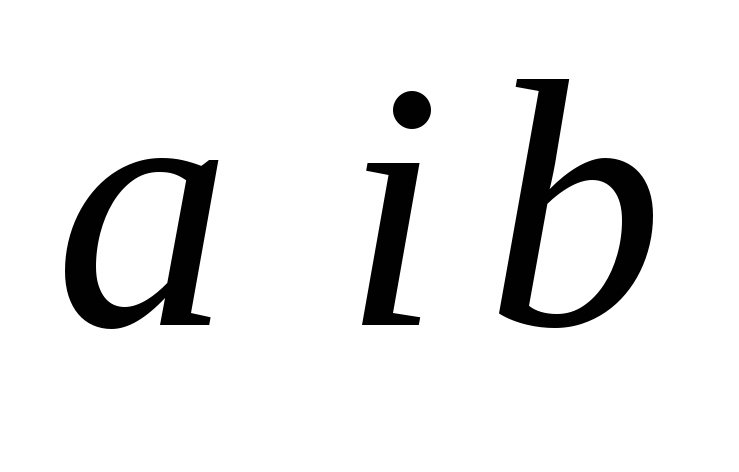із того, що 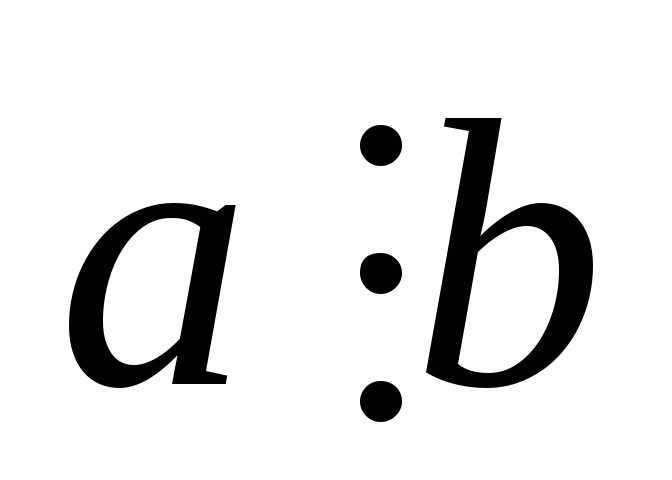не випливає, що .

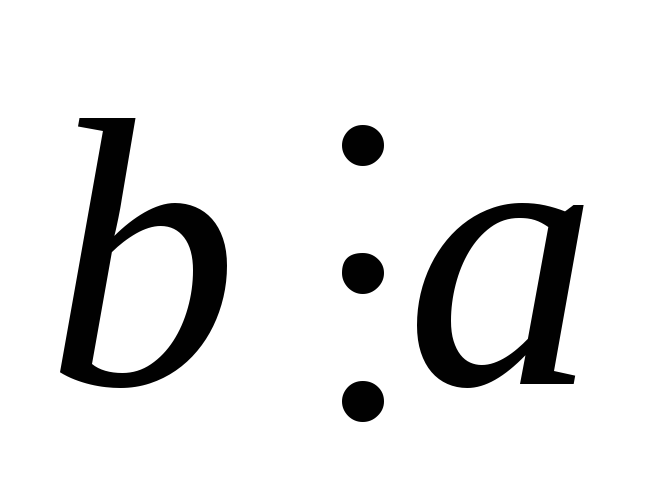   3. Із того, що 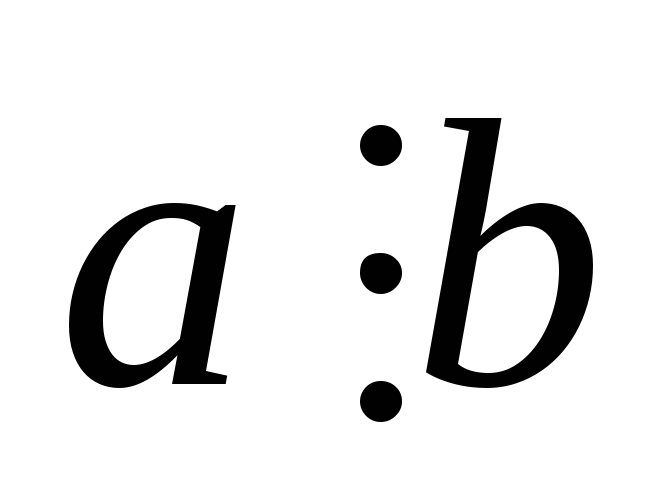і 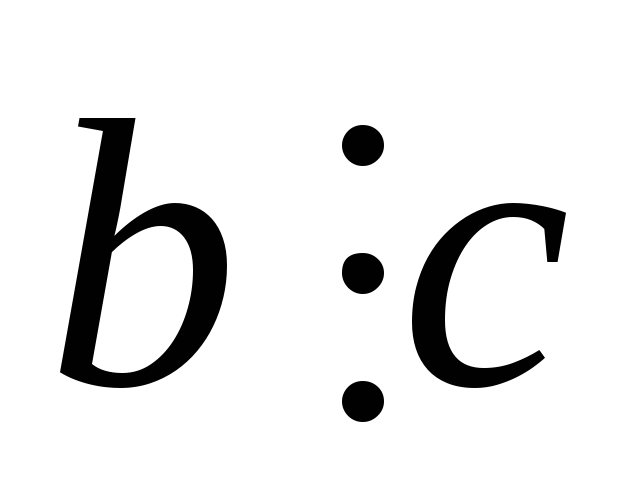, випливає, що .

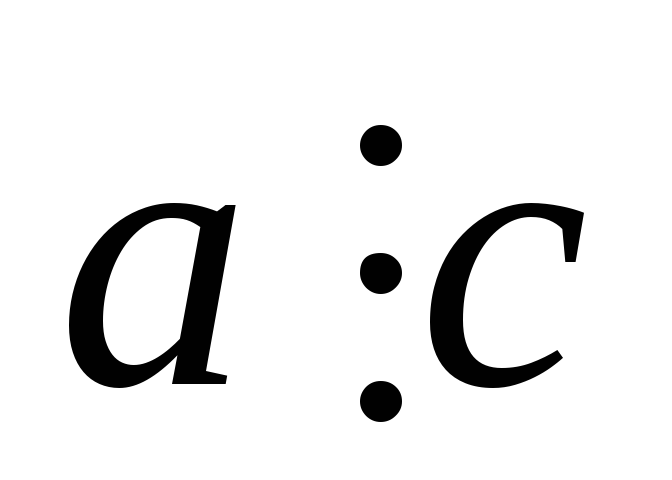3. Подільність суми, різниці і добутку цілих невід‘ємних чисел.

   1. теорема про подільність суми. Якщо кожний доданок ділиться на натуральне число 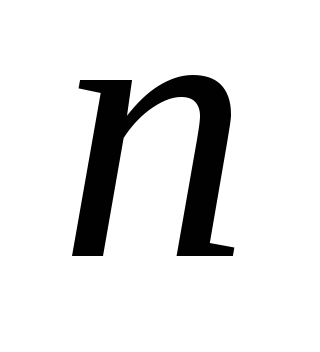, то і сума ділиться на це число. Наприклад, 114+348+908 ділиться на 2? Так як .

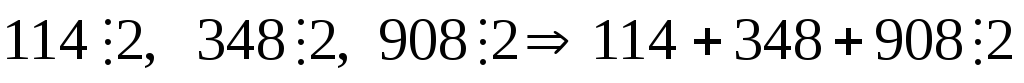   2. теорема про подільність різниці. Якщо числа 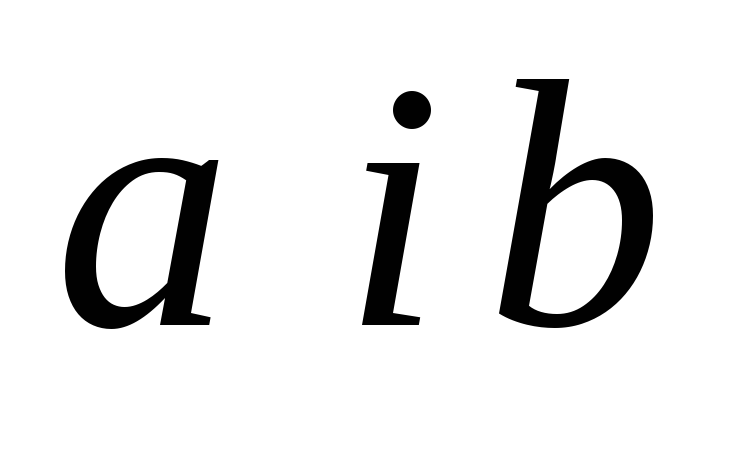діляться на число 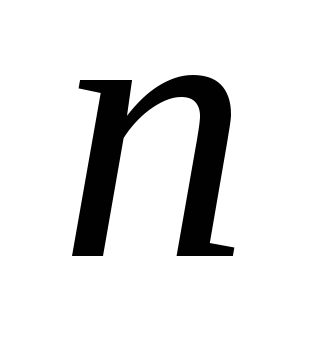і 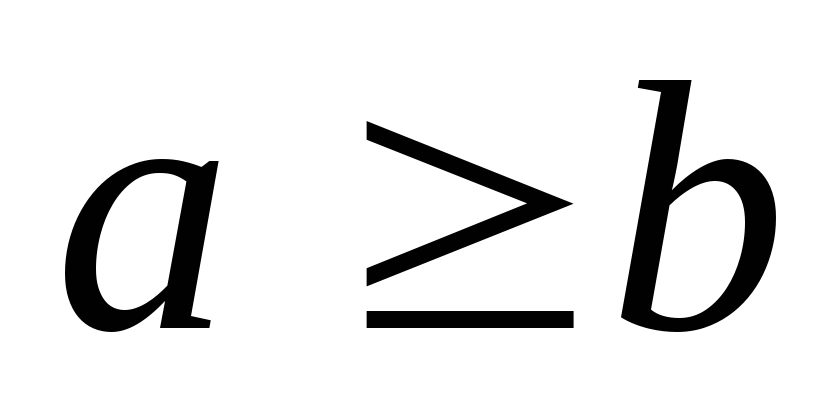, то їх різниця .

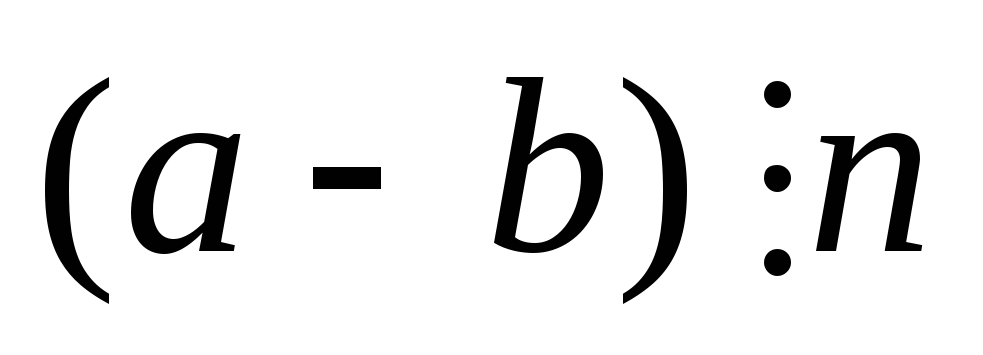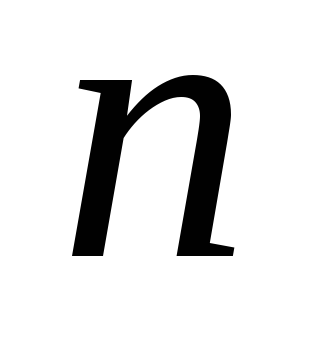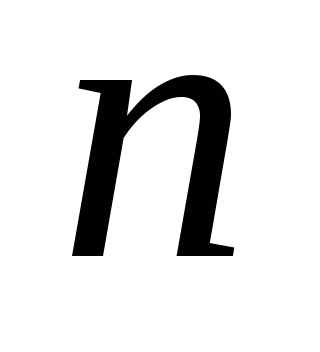   3. теорема про подільність добутку. Якщо один з множників добутку ділиться на число , то і весь добуток ділиться на число . Наприклад, 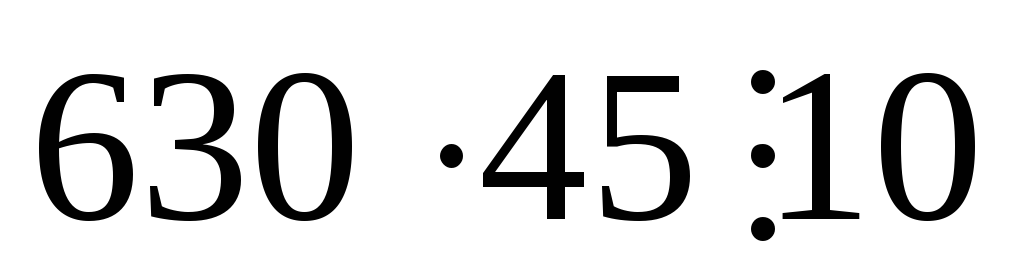?. Так як .

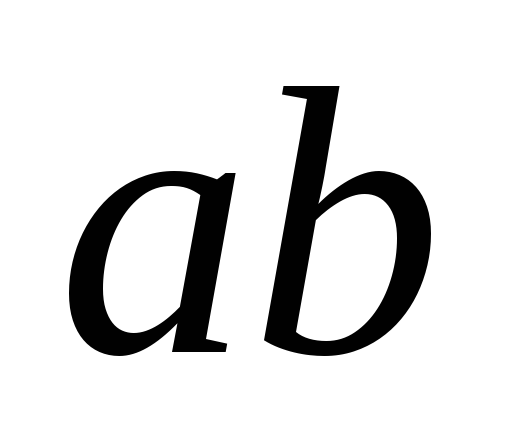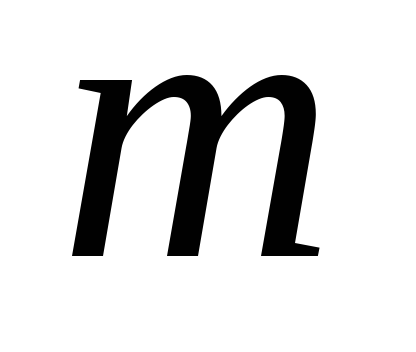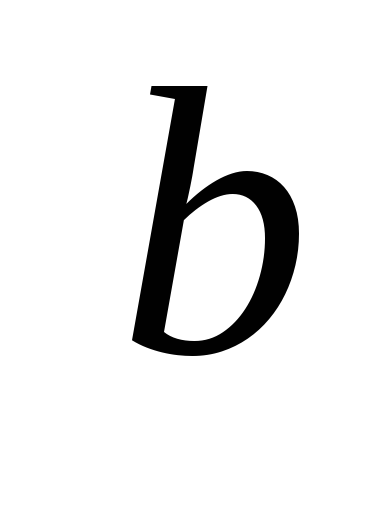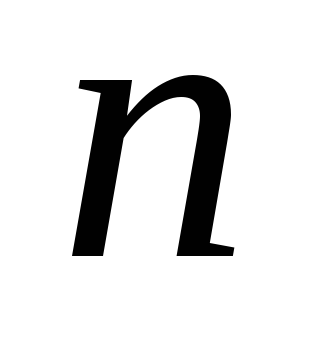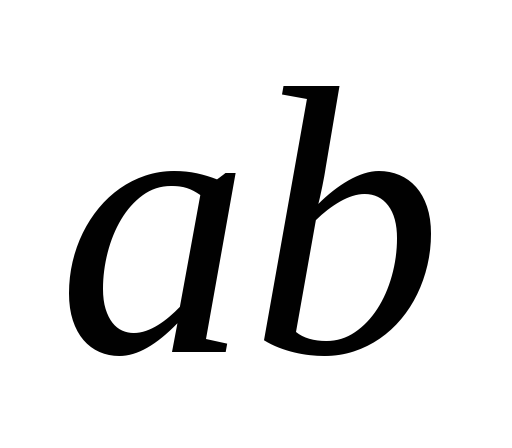   4. Якщо в добутку чисел множник ділиться на число , а число на число , то добуток ділиться на добуток 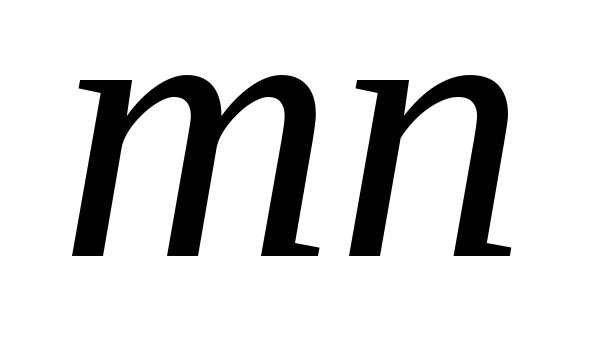. Наприклад, ?. Число , тоді 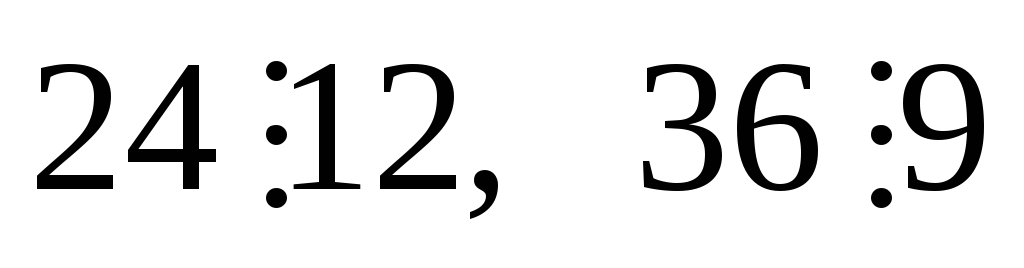, значить .

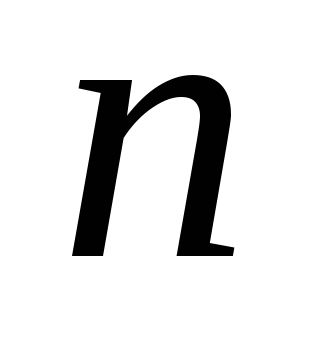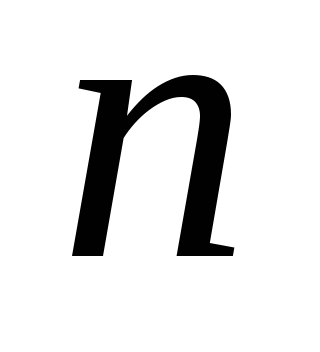   5. Якщо в сумі один доданок не ділиться на число , а решта доданків ділиться , то вся сума не ділиться на число . Наприклад, 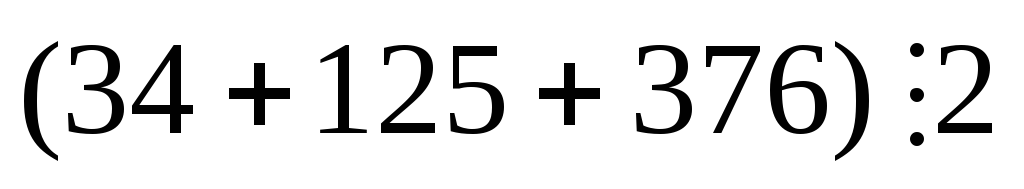? Так як число 125 не ділиться на 2, значить вся сума не ділиться на 2.

4. Признаки подільності чисел.

Ознака подільності на 2: Для того, щоб число ділилося на 2, необхідно і достатньо, його десятковий запис закінчувався цифрою 0,2,4,6,8.

Ознака подільності на 5: Для того, щоб число ділилося на 5, необхідно і достатньо, його десятковий запис закінчувався цифрою 0 або 5.

Ознака подільності на 4: Для того, щоб число ділилося на 4, необхідно і достатньо, щоб на 4 ділилось двозначне число, яке утворене останніми двома цифрами десяткового запису числа.

Ознака подільності на 3, 9: Для того, щоб число ділилося на 3, 9, необхідно і достатньо, щоб сума цифр його десяткового запису ділилася на 3, 9.

Ознака подільності на 10: Для того, щоб число ділилося на 10, необхідно і достатньо, щоб десятковий запис числа закінчувався цифрою 0.