Правила віднімання числа з суми і суми із числа:

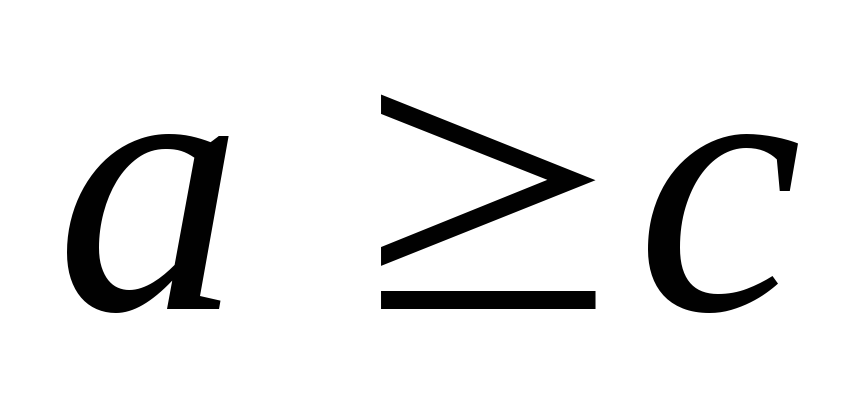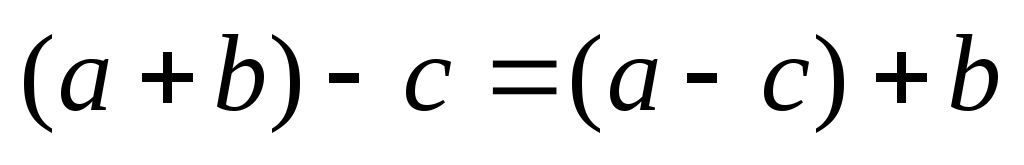• Щоб відняти число від суми, достатньо відняти його з одного з доданків і до отриманого результату додати інший доданок: а) якщо , то , б) якщ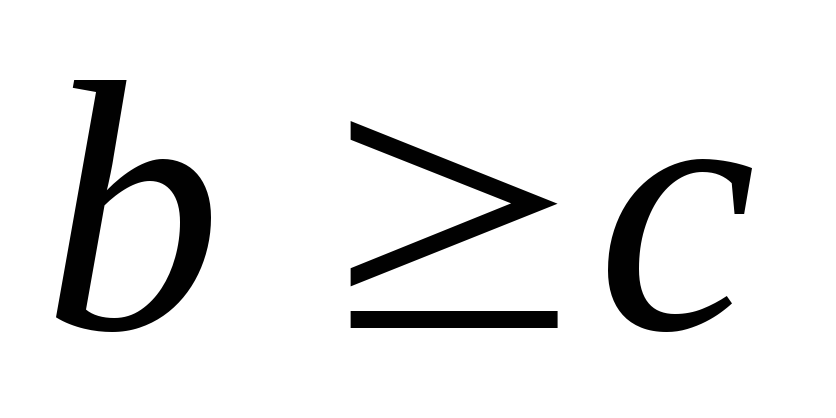о , то .

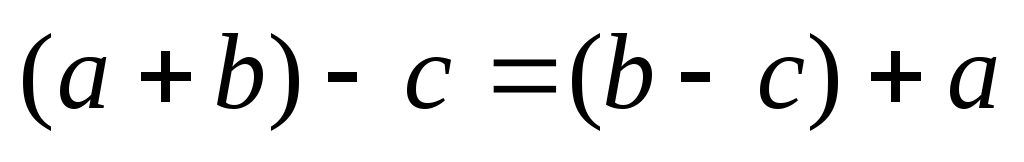• Щоб відняти від числа суму чисел, достатньо відняти від цього числа послідовно доданки: .

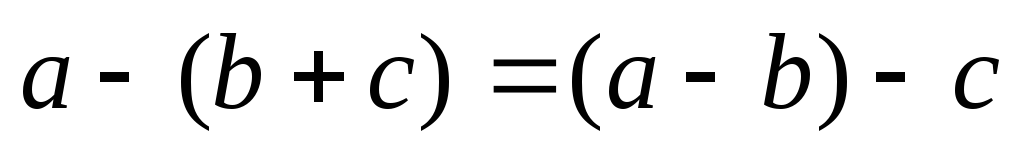3. Множення.

Задача: «На кожне дитяче пальто потрібно пришити по 4 ґудзика. Скільки ґудзиків знадобиться для 6 пальт?».

Добутком чисел і називається таке число с=, яке задовольняє умовам:

1) (раз) при 1.

2)

3) .

Дія за допомогою якої знаходять добуток чисел називається множенням, а компоненти: перший множник, другий множник, добуток.

Добуток чисел і можна розглядати як кількість елементів декартового добутку множин А іВ.

Добуток існує і тільки один.

Закони множення:

Комутативний (переставний)- ,

Асоціативний (сполучний)- ,

Дистрибутивний (розподільний) по відношенню до додавання і по відношенню до віднімання .

Наприклад, користуючись законами множення обчислити значення виразу: .

4. Ділення.

Припустимо і множина А розбита на підмножини, які не перетинаються. Якщо - число підмножин в розбитті множини А, то часткою чисел і називають число елементів кожної підмножини. Наприклад, «8 апельсинів розклали по 2 на кожну тарілку. Скільки знадобиться тарілок?». Якщо - число елементів кожної підмножини в розбитті множини А, то часткою чисел і називають число підмножин в розбитті. Наприклад, «12 олівців роздали 3 учням порівну. Скільки олівців отримав кожний?».

Дія за допомогою якої знаходять частку називають ділення, а компоненти: ділене, дільник, частка.

Правильність ділення перевіряється множенням.

Часткою чисел і називається число с=, добуток якого з числом дорівнює : .

Щоб частка існувала необхідно, щоб . Якщо частка існує, то вона єдина. На нуль ділити не можна.

Щоб знати, у скільки разів одне число більше за інше, необхідно більше число поділити на менше. Наприклад, «У Каті 6 зошитів, а у Дмитра в два рази менше. Скільки зошитів у Дмитра?» і «Купили 3 парти і 12 стільців. У скільки раз менше купили парт, ніж стільців?».

Правило ділення суми на число: якщо числа і діляться на число с, то їх сума ділиться на число с; частка, яку отримують при діленні суми + на число с, дорівнює сумі часток, які отримують при діленні числа на с і числа на с: .

Правило ділення числа на добуток: якщо число ділиться на числа і с , то щоб поділити число на добуток , достатньо поділити число на число або на число с і отриману частку поділити на число с або на число . .

Правило добутку числа на частку: щоб помножити число на частку чисел, достатньо помножити це число на ділене і отриманий добуток поділити на дільник: .

5. Ділення з залишком.

Число 37 на 8 не ділиться, але існують такі числа 4 і 5, що . Поділити число з залишком на інше число – це значить знайти такі цілі невід‘ємні числа і , що . Залишок обов‘язково має бути меншим дільника.

Лекція 11,12. Подільність чисел.

Мета:

План:

1. Поняття відношення подільності.

2. Властивості відношення подільності.

3. Подільність суми, різниці і добутку цілих невід‘ємних чисел.

4. Признаки подільності чисел.

5. Найбільший спільний дільник і найменше спільне кратне.

6. Признаки подільності на складові числа.

7. Знаходження НСД і НСК чисел способом розкладу на прості множники.

8. Алгоритм Евкліда.