Погрешность величины, не измеряемой в ходе эксперимента
Часто в лабораторных работах используют значения некоторых величин, измеренных заранее (данные установки), а также табличные данные и т. п. без указания погрешности. В таких случаях абсолютную погрешность принимают равной половине единицы наименьшего разряда, представленного в числе.
Примеры.
1.
Масса тела m
= 532,8 г (прямое измерение не проводилось),
тогда m = 
0,1
= 0,05 г. Следовательно, m
= (532,8
0,05) г.
2. Ускорение свободного падения g = 9,81 м/с2 (табличная величина).
Абсолютная
погрешность g
=
0,01
= 0,005 м/с2,
тогда g
= (9,81
0,005) м/с2.
3. Трансцендентное число 3,1415926… . Округляя число , т. е. заменяя на приближенное значение пр, допускаем погрешность = пр, которая в зависимости от требуемой точности принимает следующее значение:
если
пр
= 3,14, то
=
0,01=
0,005, а
=
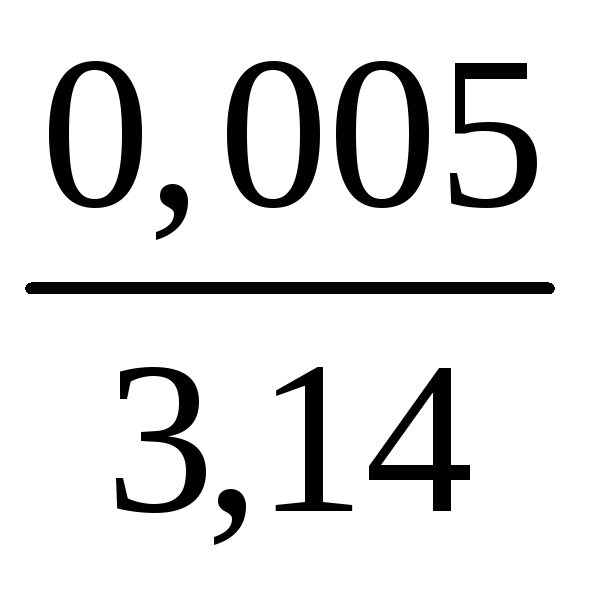100
% = 0,16 %;
если
пр
= 3,142, то
=
0,001=
0,0005, а
=
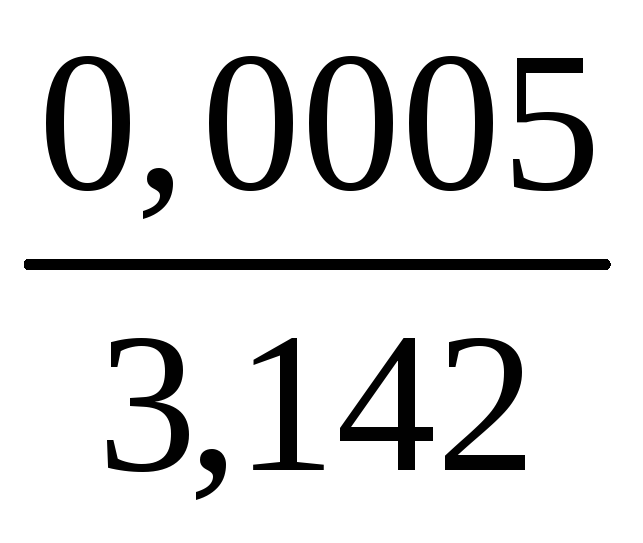100
% = 0,016 %.
Приложение 4
Понятие о частных производных
Пусть дана функция нескольких переменных f = f(x, у, z, …). Если зафиксировать значение всех независимых переменных, кроме одной, то f станет функцией этой одной переменной и по ней можно брать производную по известным правилам. Такие производные называются частными. Другими словами,
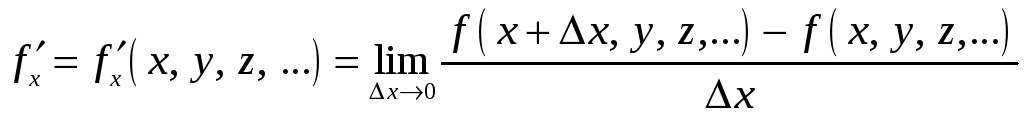– частная
производная по переменной х
от функции f,
– частная
производная по переменной у
от функции f,
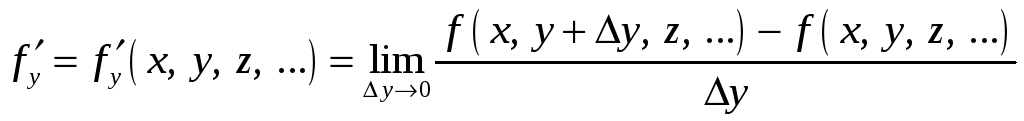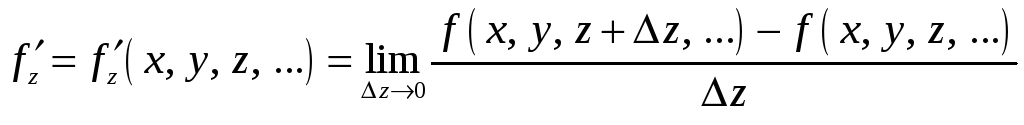– частная
производная по переменной z
от функции f
и т. п.
Символы
или
(x,
y,
z,
…) для функций нескольких переменных
не имеют смысла, так как небходимо
обязательно указывать, по какой именно
переменной производится дифференцирование.
Частная производная (например, по х)
обозначается:
;
;
(
x,
y,
z,
…),
однако первые два обозначения из них предпочтительнее.
Отметим, что правила вычисления частных производных от конкретных функций совпадают с правилами, применяемыми для функций одной переменной, только требуется каждый раз помнить, по какой переменной берется производная, а к остальным переменным относиться как к постоянным.
Примеры.
Дана функция нескольких переменных; требуется найти частные производные по всем переменным.
1. f(x, y) = x2sin y.
=
2xsin y
(здесь y
рассматривается как постоянная);
=
x2соs y
(здесь х
рассматривается как постоянная).
2. f = xy.
=
yxy–1
(здесь y
рассматривается как постоянная);
=
xyln x
(здесь х
рассматривается как постоянная).
3.
f
= x2
+ z2
+ xz3
–
.
=
2x
+ z3
(здесь z
и y
рассматриваются как постоянные);
=
(здесь х
и z
рассматриваются как постоянные);
=
2z
+ 3xz2
–
(здесь х
и y
рассматриваются как постоянные).
Приложение 5
Численное дифференцирование
Пусть
дана функция f
= f (x).
Производная функции
в точке x
в
соответствии с определением задается
следующим выражением:
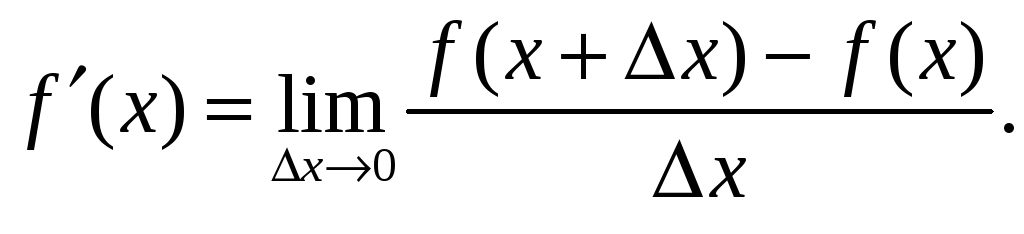
Приближенное
значение производной
в точке x
может быть найдено по двум значениям
функции, одно из которых вычислено
непосредственно в точке x,
а другое – в точке x+∆x,
расположенной вблизи x:
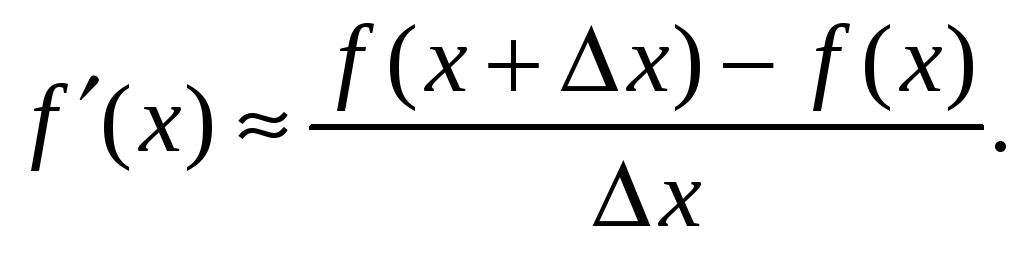
В том случае, когда дана функция нескольких переменных f = f (x, у, z, …), подобным образом вычисляются частные производные:
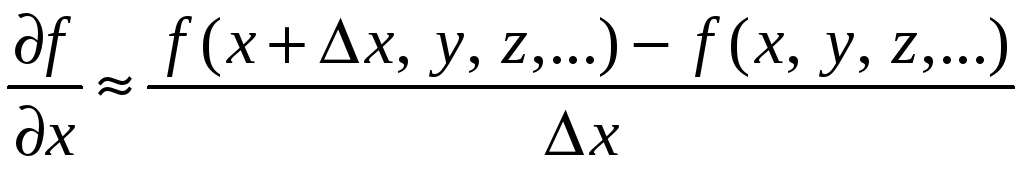– частная
производная по переменной х
от функции f,
– частная
производная по переменной y
от функции f,
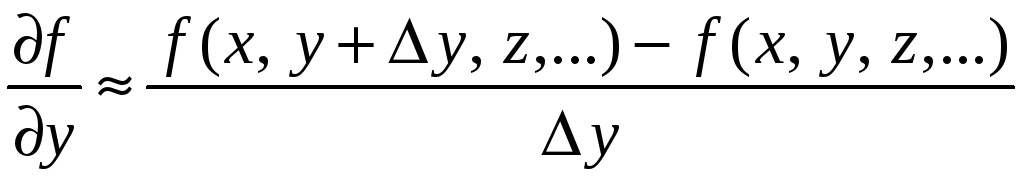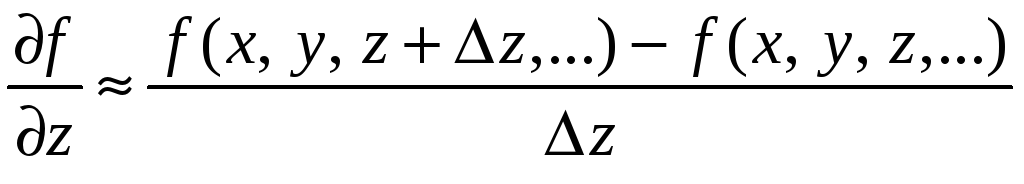– частная
производная по переменной z
от функции f
и т.п.
Учебное издание
КРОХИН Сергей Николаевич,
ЛИТНЕВСКИЙ Леонид Аркадьевич,
МИНАБУДИНОВА Сания Анасовна
Измерения и расчет погрешностей
в лабораторном практикуме по физике
_________________
Редактор Т. С. Паршикова
* * *
Подписано в печать . . 2011. Формат 6084 1/16.
Плоская печать. Бумага офсетная.
Усл. печ. л. , . Уч.-изд. л. , . Тираж 1000 экз.
Заказ .
* *
Редакционно-издательский отдел ОмГУПСа
Типография ОмГУПСа
*