
- •Моделирование химико-технологических процессов
- •Оглавление
- •Введение, основные понятия и определения
- •1. Методы моделирования и область их применения
- •1.1. Физическое моделирование (фм)
- •1.2. Математическое моделирование (мм)
- •2. Основные принципы и направления при построении и решении математических моделей
- •2.1. Составление математической модели
- •2.2. Нахождение решения математической модели
- •2.3. Проверка моделей на адекватность
- •3. Математическое описание структуры потока в аппарате – основа построения моделей
- •3.1. Методы исследования структуры потоков
- •3.2. Основные характеристики функции распределения потока по времени пребывания в аппарате
- •4. Типовые модели структуры потока
- •4.1. Модель идеального перемешивания
- •4.2. Модель идеального вытеснения
- •4.3. Ячеечная модель
- •4.4. Ячеечная модель с рециркуляцией
- •4.5. Диффузионная модель
- •4.6. Сравнение аппаратов соответствующих моделям ип и ив
- •5. Методы статистического анализа эксперимента
- •5.1. Основные характеристики случайных величин
- •5.2. Равномерное распределение
- •5.3. Нормальное распределение
- •5.4. Доверительные интервалы и доверительная вероятность, распределение Стьюдента
- •5.5. Определение общей дисперсии для серии параллельных опытов
- •5.6. Оценка дисперсии нормально распределенной случайной величины
- •5.7. Проверка однородности результатов измерений
- •6. Планирование эксперимента
- •6.1. Основные понятия и определения
- •6.2. Выбор области проведения эксперимента
- •6.3. Полный факторный эксперимент (пфэ)
- •6.4. Дробный факторный эксперимент
- •7. Оптимизация эксперимента
- •8. Планы второго порядка
- •8.1. Центральное композиционное планирование
- •8.2. Ортогональный план второго порядка
- •8.3. Ротатабельный план второго порядка
- •Список литературы
- •Приложение 1. Квантили нормального распределения
- •Приложение 2. Квантили распределения Пирсона
- •Приложение 3. Значения параметра для различных уровней значимости и степеней свободы
- •Приложение 4. Квантили распределения Стьюдента
- •Приложение 6. Пример использования модели ип для описания процесса непрерывной массовой кристаллизации
- •Приложение 7. Примеры использования типовых моделей для описания процесса теплообмена
- •Лицензия лр № 020370
5.2. Равномерное распределение
Равномерным называется распределение, для которого плотность вероятности f(x) постоянна в определенных пределах и равна нулю вне этих пределов (рис. 5.4),
|
|
Другими словами равномерным называется распределение такой случайной величины, появление любого значения которой равновероятно.
Так как площадь, ограниченная кривой распределения, равна единице c(b – a) = 1, то в формуле (5.27) с = 1/(b – a).
Функция распределения (рис. 5.5) задается выражением:
|
|
|
|
|
|
Рис. 5.4. Плотность вероятности равномерного распределения |
Рис. 5.5. Функция равномерного распределения |
Математическое ожидание равномерно распределенной случайной величины Х определяется как
|
|
В силу симметричности равномерного распределения медиана величины Х также определяется как х0,5 = (a + b)/2. Дисперсия случайной величины Х
|
|
5.3. Нормальное распределение
Случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения имеет вид
|
|
где – < x < .
Функция распределения
|
|
Плотность и функция распределения нормированной случайной величины соответственно определяются как
|
|
|
|
Нормальное распределение нормированной случайной величины называется стандартным.
Графики плотности и функции нормального распределения нормированной случайной величины приведены на рис. 5.6, а, б.
Нормальное распределение наиболее часто встречается на практике и теоретически наиболее полно разработано. Нормальный закон при некоторых условиях является предельным законом для суммы большого числа n независимых случайных величин, каждая из которых подчинена какому-либо закону распределения. Основное ограничение состоит в том, чтобы все слагаемые играли в общей сумме относительно малую роль. Если у явлений множество событий происходит случайно вследствие воздействия на них большого числа независимых (или слабо зависимых) факторов, то закон распределения таких явлений близок к нормальному. Нормальный закон распределения широко используется при обработке наблюдений.

|
а |
б |
Рис. 5.6. Плотность (а) и функция (б) нормального распределения
Нормальное распределение содержит минимум информации по сравнению с любыми распределениями с той же дисперсией. Следовательно, замена некоторого распределения эквивалентным нормальным не может привести к переоценке точности наблюдений. График плотности распределения называется нормальной кривой или кривой Гаусса.
Функция
|
Ф(х) = F0(x) – 0,5 (5.35) |
называется функцией Лапласа,
|
|
Функция Лапласа – нечетная функция, т.е. Ф(–х) = –Ф(х), поэтому таблицы значений Ф(х) составлены только для х > 0.

 .
(5.28)
.
(5.28)
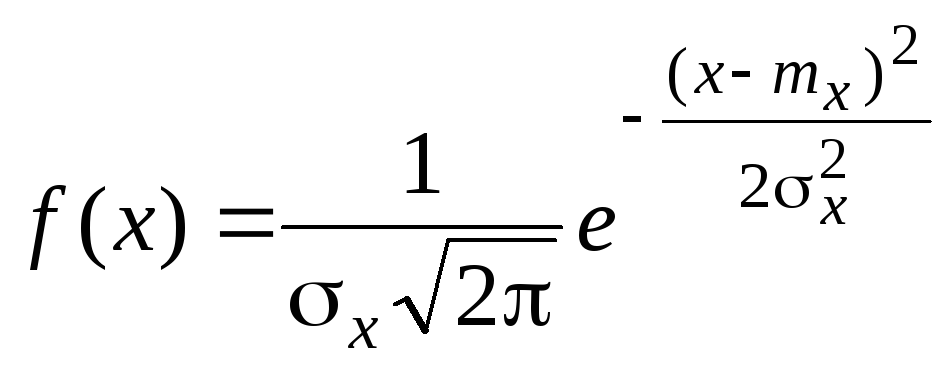 ,
(5.31)
,
(5.31) .
(5.32)
.
(5.32) .
(5.36)
.
(5.36)