
- •Міністерство освіти і науки україни національна металургійна академія україни
- •Б.Б. Потапов тепломассообмен Днепропетровск нМетАу 2009
- •Раздел 1. Введение в теорию теплообмена
- •1.1. Способы и механизмы переноса теплоты
- •Перенос теплоты теплопроводностью
- •1.1.2. Перенос теплоты конвекцией
- •1.1.3. Излучение
- •1.2. Основные понятия и определения
- •1.3. Основные законы переноса теплоты.
- •1.3.1. Теплопроводность
- •1.3.2. Конвективный теплообмен
- •1.3.3. Лучистый теплообмен
- •1.3.4. Теплопередача
- •Раздел 2. Теплопроводность
- •2.1. Общие положения теории теплопроводности
- •2.1.1. Теплопроводность веществ
- •2.1.2. Дифференциальное уравнение теплопроводности Фурье и условия однозначности
- •2.2. Теплопроводность и теплопередача при стационарном режиме
- •2.2.1. Теплопроводность и теплопередача через плоскую стенку
- •2.2.2. Влияние переменности на распределение температуры в пластине
- •2.2.3. Теплопроводность и теплопередача в цилиндрической стенке
- •2.2.4. Критический диаметр цилиндрической стенки
- •2.2.5. Теплопередача через стенки произвольной формы
- •2.2.6. Пути интенсификации теплопередачи
- •2.3. Теплопроводность при нестационарном режиме
- •2.3.1. Решение задач нестационарной теплопроводности методом разделения переменных
- •2.3.2. Исследование решения уравнения теплопроводности при условии
- •2.3.3. Исследование решения дифференциального уравнения теплопроводности при
- •2.3.4. Метод расчета нагрева(охлаждения) тел по графикам
- •2.3.5. Охлаждение тел конечных размеров.
- •Конечной длины
- •В уравнении множители правой части находятся по формулам или графикам, причем в качестве определяющих линейных размеров берется половина высоты цилиндра Rz и радиус цилиндра r0.
- •2.3.6. Численные методы решения задач теплопроводности
- •Решение дифференциального уравнений теплопроводности мкр для граничных условий II рода.
- •2.3.7. Приближенные методы решения задач теплопроводности
- •Метод тепловой диаграммы. В основу метода тепловой диаграммы положено уравнение теплового баланса для всего нагреваемого тела.
- •Раздел 3. Конвективный теплообмен
- •3.2. Элементы теории подобия
- •3.2.1. Числа гидродинамического подобия
- •3.3. Теплообмен при естественной конвекции
- •3.3.1. Аналитическое решение задачи теплообмена при свободном ламинарном движнии вдоль вертикальной пластины
- •3.3.2. Теплообмен при свободной конвекции в большом объеме
- •3.3.3.Теплообмен при свободном движении в ограниченном пространстве
- •3.4. Вынужденная конвекция при течении жидкости в трубах и каналах
- •3.4.1. Теплоотдача при ламинарном режиме течения
- •3.4.2. Теплоотдача при турбулентном режиме течения
- •3.4.3. Теплоотдача при переходном режиме движения жидкости
- •3.4.4. Теплоотдача при течении жидкости в изогнутых трубах
- •3.4.5. Теплообмен при продольном омывании труб
- •Теплообмен при поперечном обтекании труб
- •3.6. Теплообмен при поперечном обтекании пучков труб
- •3.7. Теплообмен при обтекании плоской поверхности
- •3.8. Теплообмен при кипении
- •3.8.2. Закономерности зарождения, роста, отрыва и движения паровых пузырей
- •3.8.3. Кривая кипения
- •3.8.4. Кипение жидкости в большом объеме
- •3.8.5. Кризисы кипения
- •3.8.6. Пузырьковое кипение при вынужденной конвекции
- •3.8.7. Теплообмен при плёночном режиме кипения
- •3.9. Теплообмен при конденсации пара
- •3.9.1. Характеристика процесса конденсации
- •3.9.2.Основные уравнения подобия и расчетные формулы
- •3.9.3. Влияние на теплоотдачу при конденсации различных факторов
- •4.Теплообмен излучением
- •4.1. Общие положения лучистого теплообмена
- •4.1.1. Описание процесса
- •4.1.2. Определение основных понятий
- •4.1.3. Поглощательная, отражательная и пропускательная способность тела
- •4.1.4 Эффективное и результирующее излучение
- •4.1.5. Основные законы теплового излучения
- •4.2. Угловые коэффициенты и методы их определения
- •4.3. Лучистый теплообмен между телами, разделенными прозрачной средой
- •4.3.1. Теплообмен обособленного тела с окружающей средой
- •4.3.2. Лучистый теплообмен между двумя поверхностями, образующих замкнутую систему
- •4.3.3. Теплообмен излучением при наличии экрана
- •4.3.4. Лучистый теплообмен между “n” поверхностями, образующими замкнутую систему
- •4.4. Теплообмен излучением в поглощающей газовой среде
- •4.4.1. Особенности поглощающих и излучающих сред
- •4.4.2. Лучистый теплообмен между газом и оболочкой
- •4.4.3. Теплообмен излучением между двумя поверхностями, разделенными поглощающим газом
- •4.5. Особенности теплообмена излучением в металлургических печах
- •4.6. Радиационно-конвективный теплообмен и теплопередача
- •Раздел 5. Теплообменные аппараты
- •5.1. Общие положения
- •5.2. Основы теплового расчета рекуперативных теплообменников
- •5.2.1. Уравнение теплового баланса рекуператора
- •5.2.2. Уравнение передачи теплоты в рекуперативном теплообменнике
- •5.2.3. Определение средней разности температур между греющим и нагреваемым теплоносителями
- •5.2.4. Конечные температуры теплоносителей
- •5.3. Основы теплового расчета регенераторов
5.2.3. Определение средней разности температур между греющим и нагреваемым теплоносителями
Рассмотрим
теплообменный аппарат, работающий по
схеме
![]() ,
,
при
этом температура горячей жидкости
понизится на
![]() ,
а холодной повысится на
,
а холодной повысится на
![]() .
Следовательно,
.
Следовательно,
![]()
откуда
![]() ;
;
![]() .
.
Изменение температурного напора на участке dF:

Обозначим
 ,
тогда уравнение примет вид:
,
тогда уравнение примет вид:
![]()

Рис 5.5. Температурные диаграммы для прямотока (а) и противотока (б)
Из этого соотношения следует:
![]() .
.
Приравняв уравнения (1) и (4), получим:
![]() ,
или
,
или
![]()
Интегрируя это уравнение, получаем:

![]()
![]()
![]()
![]()
Из последнего
выражения следует, что температурный
напор вдоль поверхности теплообмена
изменяется по экспоненциальной
зависимости. Зная этот закон, легко
установить и среднее значение
температурного напора
![]() .
На основании теоремы о среднем имеем:
.
На основании теоремы о среднем имеем:

![]()
Так как
![]() и
и
![]() ,
после подстановки этих соотношений в
последнее выражение получим:
,
после подстановки этих соотношений в
последнее выражение получим:
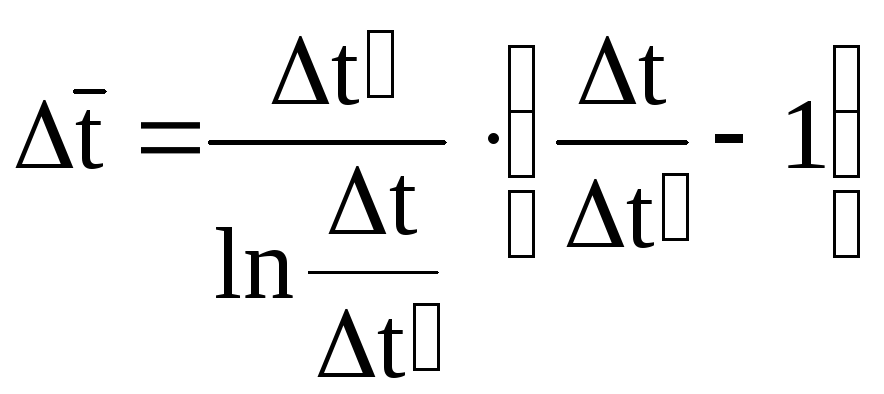 или
или

Если поверхность
теплообмена имеет конечную величину и
на выходе из теплообменника температурный
напор равен
![]() ,
то выражение для среднего температурного
напора принимает вид:
,
то выражение для среднего температурного
напора принимает вид:
 . (5.10)
. (5.10)
Здесь
![]()
![]() .
.
В раскрытом виде для теплообменника, работающего по схеме прямотока, выражение для среднего температурного напора имеет вид:
 (5.11)
(5.11)
Аналогичным образом
выводится
![]() для противотока. Однако в этом случае
для противотока. Однако в этом случае
![]() и
и
![]() и выражение для среднего температурного
напора для теплообменника, работающего
по схеме противотока, имеет вид:
и выражение для среднего температурного
напора для теплообменника, работающего
по схеме противотока, имеет вид:
 (5.12)
(5.12)
Результаты расчетов
среднего температурного напора для
всех других схем относительного движения
теплоносителей лежат между значениями
среднего температурного напора для
прямоточной и противоточной схем. В
связи с этим, для других схем движения
теплоносителей
![]() определяется по выражению
определяется по выражению
![]() , (5.13)
, (5.13)
где
![]() -средний
температурный напор при противотоке;
-средний
температурный напор при противотоке;
![]() -
коэффициент (поправка), учитывающий
разницу
-
коэффициент (поправка), учитывающий
разницу
![]() противотока и
противотока и
![]() рассматриваемой схемы. Аналитически
рассматриваемой схемы. Аналитически
![]() для сложных схем движения теплоносителей
определяется трудно. В связи с этим, для
ее нахождения построены графики
для сложных схем движения теплоносителей
определяется трудно. В связи с этим, для
ее нахождения построены графики
![]() .
Коэффициент
.
Коэффициент
![]() определяется как функция вспомогательных
параметров:
определяется как функция вспомогательных
параметров:
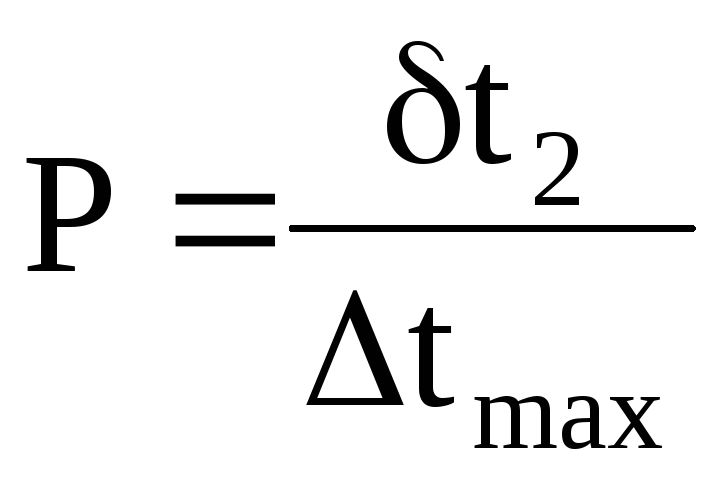 и
и

![]() ;
;
![]() ;
;
![]() .
.
5.2.4. Конечные температуры теплоносителей
При поверочном
расчете теплообменника задана поверхность
нагрева. Искомыми величинами могут
быть количество передаваемой от горячего
теплоносителя холодному и конечные
температуры теплоносителей, то есть
определить Q,
![]() ,
,
![]() .
.
Рассмотрим теплообменный аппарат, работающий по схеме прямотока. Ранее показано, что температурный напор вдоль F изменяется по экспоненциальному закону
![]()
![]() .
.
Вычтем из правой и левой части уравнения по единице
![]() .
.
Произведем
расшифровку значений
![]() и
и
![]() и выполним их подстановку в последнее
соотношение:
и выполним их подстановку в последнее
соотношение:
![]() .
.
Поменяв знаки в правой и левой части уравнения, запишем его в виде:

С учетом того, что
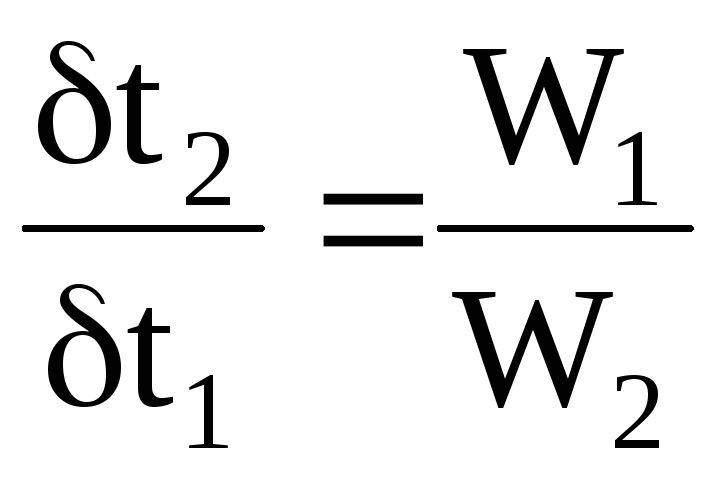 и
и
 ,
последнее уравнение принимает вид:
,
последнее уравнение принимает вид:
 ,
,
или
 . (5.14)
. (5.14)
Если обозначить
 ,
то можно записать:
,
то можно записать:
 .
.
Здесь
![]() -
безразмерное соотношение водяных
эквивалентов,
-
безразмерное соотношение водяных
эквивалентов,
![]() - безразмерная поверхность нагрева.
Таким образом в общем виде имеем:
- безразмерная поверхность нагрева.
Таким образом в общем виде имеем:
 .
.
Для удобства
практического использования многочисленные
расчеты функции
![]() обобщены в графики вида
обобщены в графики вида
 ,
рис. 5.6.
,
рис. 5.6.

Рис. 5.6. График
от
![]() kF/W1
W1/W2
для прямотока
kF/W1
W1/W2
для прямотока![]()
![]()
![]()
![]()
![]()
![]()
![]()
При известных
значениях
![]() уравнение и графики дают возможность
определить изменение температуры
греющего теплоносителя. Изменение
температуры нагреваемого теплоносителя
находится из уравнения теплового
баланса:
уравнение и графики дают возможность
определить изменение температуры
греющего теплоносителя. Изменение
температуры нагреваемого теплоносителя
находится из уравнения теплового
баланса:
![]() . (5.15)
. (5.15)
Конечные температуры теплоносителей определяются из равенств:
![]() .
.
Количество теплоты, переданной от горячего теплоносителя холодному, определяется их уравнения теплового баланса:
![]() .
.
Выведем выражение для определения конечных температур для случая противотока:
![]()
![]()
![]()
![]()
![]()

![]()
![]()

 (5.16)
(5.16)
 (5.17)
(5.17)
 .
.
Расчеты по этой зависимости также обобщены в графики, с помощью которых решается задача определения конечных температур теплоносителей при противотоке.

 .
.
Рис. 5.7. Сравнение прямотока и противотока
Из графика следует,
что прямоточная и противоточная схемы
могут быть равноценны при очень малых
и очень больших отношениях водяных
эквивалентов или очень малых значениях
параметра
![]() .
Во всех остальных случаях (особенно при
W1/W2=1)
эффективность противотока выше, чем
прямотока. Чем выше безразмерная
поверхность
.
Во всех остальных случаях (особенно при
W1/W2=1)
эффективность противотока выше, чем
прямотока. Чем выше безразмерная
поверхность
![]() ,
тем сильнее проявляется преимущество
противоточной схемы.
,
тем сильнее проявляется преимущество
противоточной схемы.
При отмеченных преимуществах противоточной схемы следует иметь в виду, что температура поверхности теплообмена в противоточных аппаратах выше, чем в прямоточных.
Рассчитать температуру стенки теплообменных элементов рекуператора можно из следующих условий (рис. 5.8.):
![]()
![]()
![]()

Рис. 5.8. Распределение температур в стенке рекуператора
Если термическим сопротивлением стенки пренебречь, то
![]() .
.
При условии стационарности процесса передачи теплоты справедливо равенство:
![]() ,
,
откуда
![]() (5.18)
(5.18)
Температуру стенки следует рассчитывать для сечения с максимальной температурой горячего и холодного теплоносителя. В противоточной схеме
это место входа горячего потока в рекуператор.
