2.3.4. Метод расчета нагрева(охлаждения) тел по графикам

Ранее показано, что решение задачи нестационарной теплопроводности при граничных условиях Ш рода имеет вид:

,

где корни определяются из решения уравнения .

Многочисленные исследования показали, что при значениях ряд представленный суммой становится настолько быстро сходящимся, что распределение температур достаточно точно описывается первым членом ряда при n=1):

(2.68)

Представим уравнение (2.68) в виде:

(2.69)

Величина является функцией только числа Bi и заранее может быть рассчитана и табулированая. Кроме того, если рассматривать температуру для определенного значения , то и является функцией только числа Bi. Конкретно для оси пластины и , а для поверхности и .

Для оси пластины произведение обозначим как некоторую функцию , тогда уравнение (2.69) можно записать в виде:

(2.70)

Для поверхности пластины произведение обозначим через и уравнение (2.69) можно записать в виде:

(2.71)

Из уравнений (2.70) и (2.71) следует, что при заданной координате безразмерная температура является функцией двух безразмерных параметров Bi и , то есть

и

Логарифмируя уравнения (2.70) и (2.71) получим:

и .

Из последних уравнений следует, что при заданном значении координаты и при заданном значении Bi натуральный логарифм безразмерной температуры линейно зависит от времени. Последнее обстоятельство позволяет представить для уравнений (2.70) и (2.71) графическое решение. В литературе представлены графические решения для пластины, цилиндра и шара.

2.3.5. Охлаждение тел конечных размеров.

Охлаждение параллелепипеда. Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой и постоянным коэффициентом теплоотдачи α на всех его гранях. В начальный момент времени (τ=0) все точки параллелепипеда имеют одинаковую температуру t₀. Параллелепипед с размерами является однородным и изотропным (рис. 2.11). Требуется найти распределение температуры для любого момента времени.

Поместим начало координат в центр параллелепипеда. При этом дифференциальное уравнение запишется следующим образом:

Начальные условия:

Граничные условия:

Условия симметричности нагрева:

Рис. 2.11. Схема для определения температуры в избранных точках

параллелепипеда

Параллелепипеды, цилиндры конечных размеров и прямоугольные стержни можно рассматривать как тела, образованные пересечением неограниченных тел. Так параллелепипед – тело, образованное пересечением трех неограниченных пластин толщиной цилиндр конечных размеров – тело, образованное пересечением неограниченного цилиндра диаметром 2r и пластиной толщиной 2R; стержень бесконечной длины – тело, образованное пересечением двух неограниченных пластин с толщиной .

Можно доказать, что решение таких задач представляется произведением безразмерных температур для тел неограниченных размеров, в результате пересечения которых образовалось рассматриваемое тело.

Как было сказано ранее, параллелепипед образован в результате пересечения трех взаимно перпендикулярных бесконечных пластин конечной толщины. Следовательно, для него и решение можно представить как произведение безразмерных температур для трех безграничных пластин:

где

Общее решение в развернутом виде запишется следующим образом:

Приведенное решение удовлетворяет как дифференциальному уравнению, так и граничным условиям, описывающим процесс теплопроводности в параллелепипеде.

Таким образом, решение задачи для параллелепипеда свелось к решению задачи для безграничной пластины конечной толщины. Последнее уравнение можно записать так:

,

или

В последнем уравнении вычисляются по решениям для граничных условий III рода, выведенных ранее, или определяются по графикам функций, построенным по этим решениям.

Охлаждение длинного прямоугольного стержня. Однородный стержень охлаждается в среде с постоянной температурой t_c и при постоянном коэффициенте теплопроводности на его поверхностях. В начальный момент времени все точки стержня имеют одинаковую температуру.

Поперечное сечение стержня представляет собой прямоугольник размерами . Такое тело можно рассматривать как результат пересечения двух пластин толщиной , условия однозначности для которых такие же, как и для образовавшегося стержня. Безразмерное температурное поле для поставленной задачи определяется произведением:

_где

Порядок расчета температур в избранных точках следующий. Температура в точке 1 устанавливается произведением решений для осей пластин толщиной 2R_x и 2R_y (рис. 2.12):

^.

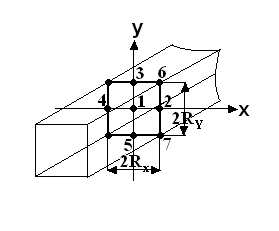
_{Рис. 2.12. Схема расположения расчетных точек в прямоугольном стержне}

_{Каждое из них определяется по графикам для оси пластины по значениям:}

.

После этого пересчетом определяется размерная температура на оси стержня:

Точка 2 находится на поверхности стержня и равно отстоит от граней (рис. 2.12). Эта точка лежит на оси пластины толщиной 2R_y и на поверхности пластины толщиной 2R_x . Поэтому температура в точке 2 определяется произведением соответствующих решений:

Значение определяется по графику для поверхности пластины по значениям , а значение определяется по графику для середины пластины по значениям . По значению пересчетом определяется размерная температура в точке 2:

Температура в точке 6 определяется произведением:

_.

Далее расчет выполняется по приведенному выше алгоритму.

Охлаждение цилиндра конечной длины. Однородный цилиндр диаметром 2r₀ и длиной 2R_z охлаждается в среде с постоянной температурой t_c (рис.2.13). Коэффициент теплоотдачи α на основаниях цилиндра и его боковой поверхности одинаков. В начальный момент времени все точки цилиндра имеют одинаковую температуру t₀. Найти распределение температуры в цилиндре в любой момент времени.

Рис. 2.13. Схема расположения расчетных точек в цилиндре