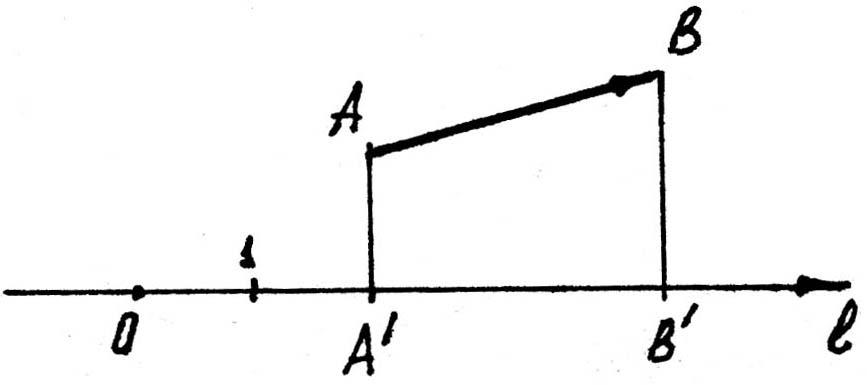
Проекция вектора на ось

Ориентированной осью называется прямая, на которой закреплена точка - начало отсчета, выбрана единица длины и направление отсчета.

Рис. 6

Проекцией вектора на ось называется величина, численно равная длине отрезка между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от к совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.

Углом между осью и вектором называется угол, на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что .

Свойства проекции вектора на ось.

1. Проекция равна нулю тогда и только тогда, когда вектор перпендикулярен оси (говорят, вектор ортогонален оси).

2. При параллельном переносе вектора его проекция не меняется.

3. Проекция вектора на ось равна произведению длины вектора на

косинус угла между вектором и осью.

.

Рис. 7 Рис. 8

В этой формуле знак проекции регулируется знаком косинуса:

- если острый угол (рис. 7), то и ;

- если тупой угол (рис. 8), то и .

4. Скалярный множитель можно выносить за знак проекции

.

5. Проекция суммы векторов равна сумме проекций слагаемых

.

Декартова прямоугольная система координат

Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единицам.

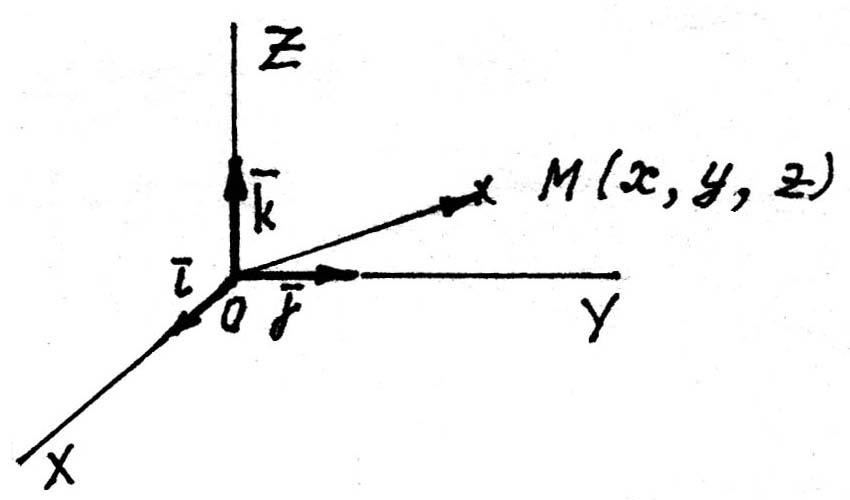Система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.

Рис. 9

Б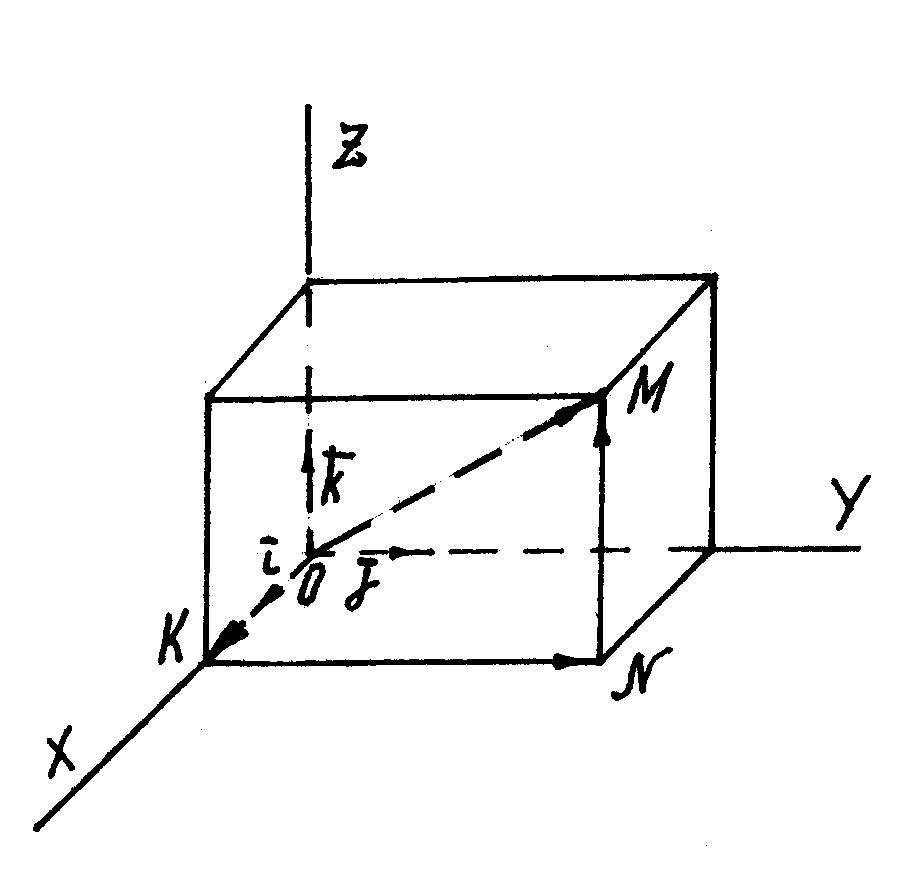азисные векторы такой системы называются ортами и обозначаются соответственно , , (рис. 9). Оси идущие в направлении базисных векторов соответственно OX – ось абсцисс, OY – ось ординат, OZ – ось аппликат. Система координат называется правой, если кратчайший поворот первого базисного вектора до совмещения со вторым базисным вектором смотрится с конца третьего базисного вектора происходящим против хода часовой стрелки. В противном случае имеем левую систему координат. Нетрудно видеть (рис. 10), что координатами вектора , равно как и точки М, являются проекции на координатные оси.

Рис. 10

Тогда , аналогично , . Теперь радиус-вектор или , где – координаты радиус-вектора , а ,, - составляющие или компоненты этого вектора. .

Поскольку, например, , а . Теперь . , где - угол между вектором и осью OX. Теперь , аналогично , , где и - углы между и осями OY и OZ соответственно. Приведенные косинусы называются направляющими косинусами радиуса вектора .

Если - произвольный вектор и X, Y, Z – его проекции на оси, то перенося начало в точку О, будем иметь , , , , .

Если вектор задан координатами начала и конца , то и расстояние между точками А и В будет .