
- •Міністерство науки і освіти, молоді та спорту України
- •Квадратичні форми.
- •Передмова
- •Лекція 1 Тема: Квадратичні форми План:
- •Алгоритм зведення квадратичної форми до канонічного виду методом Лагранжа.
- •Лекція 2 Тема: Закон інерції квадратичних форм План:
- •Лекція 3 Тема: Ортогональне перетворення квадратичної форми до канонічного виду
- •Лекція 4 Тема: Застосування квадратичних форм до дослідження алгебраїчних рівнянь другого степеня План:
- •Лекція 5 Тема: Квадратична форма в трьохвимірному просторі та її застосування до дослідження рівнянь поверхонь другого порядку План:
- •Лекція 6 Тема: Системи лінійних нерівностей
- •Лекція 7 Тема: Системи лінійних нерівностей
- •Короткий зміст лекції:
- •Система лінійних нерівностей
- •Лекція 8 Тема: Системи лінійних нерівностей План:
- •Лекція 9 Тема: Невід’ємні розв’язки системи лінійних нерівностей План:
- •Лекція 10 Тема: Принцип граничних розв’язків системи лінійних нерівностей План:
- •Лекція 11 Тема: Задачі лінійного програмування План:
- •Лекція 12 Тема: Взаємно двоїсті задачі лінійного програмування
- •Лекція 13 Тема: Симплекс-метод розв’язування канонічної задачі лінійного програмування
- •Контрольні питання для самоперевірки:
- •Лекція 14 Тема: Знаходження невід’ємних розв’язків системи лінійних рівнянь симплекс-методом План:
- •Лекція 15 Тема: Знаходження невід’ємних розв’язків системи лінійних нерівностей симплекс-методом
Лекція 7 Тема: Системи лінійних нерівностей
План:
-
Теорема Мінковського.
-
Критерії несумісності систем лінійних нерівностей.
-
Узагальнення теореми Кронекера‑Капеллі.
Короткий зміст лекції:
Нехай
система
![]() ,
сумісна і всі її розв’язки задовольняють
нерівності
,
сумісна і всі її розв’язки задовольняють
нерівності
![]() тоді ця нерівність називається наслідком
даної системи.
тоді ця нерівність називається наслідком
даної системи.
Теорема
Мінковського.
Якщо лінійна нерівність
![]() є наслідком системи однорідних лінійних
нерівностей
є наслідком системи однорідних лінійних
нерівностей
![]() ,
то існують дійсні невід’ємні числа
,
то існують дійсні невід’ємні числа
![]() ,
для яких виконується тотожне відносно
,
для яких виконується тотожне відносно
![]() співвідношення
співвідношення
![]() .
.
З цієї теореми випливають наступні критерії несумісності та сумісності систем лінійних нерівностей.
Критерій Александрова:
Система лінійних нерівностей

несумісна (нерозв’язна) тоді і тільки тоді, коли існують невід’ємні розв’язки системи лінійних нерівностей:

Критерій Вороного:
Система однорідних лінійних нерівностей

несумісна тоді і тільки тоді, коли система рівнянь

має додатній розв’язок.
Критерій Чернікова:
Система
лінійних нерівностей
![]() ,
рангу
,
рангу
![]() несумісна тоді і тільки тоді, коли хоча
б для одного відмінного від нуля мінору
r-ого
рангу порядку ∆ її матриці будь-який
супровідний його визначник цієї системи
несумісна тоді і тільки тоді, коли хоча
б для одного відмінного від нуля мінору
r-ого
рангу порядку ∆ її матриці будь-який
супровідний його визначник цієї системи
![]() або дорівнює нулю, або співпадає з ним
за знаком (тобто
або дорівнює нулю, або співпадає з ним
за знаком (тобто
![]() ).
Супровідні визначники
).
Супровідні визначники
![]()
![]() ,
одержуються з визначника ∆ оторочуванням
його знизу та праворуч відповідно
елементами j-ого
рядка матриці системи і відповідними
цим рядкам елементами стовпця вільних
членів.
,
одержуються з визначника ∆ оторочуванням
його знизу та праворуч відповідно
елементами j-ого
рядка матриці системи і відповідними
цим рядкам елементами стовпця вільних
членів.
З
критерію Чернікова випливає, що якщо
система лінійних нерівностей
![]() ,
,
![]() рангу
рангу
![]() сумісна, то сумісна і кожна визначена
нею система
сумісна, то сумісна і кожна визначена
нею система
![]() рангу r.
рангу r.
Узагальнення теореми Кронекера‑Капеллі:
Нехай
![]() – ранг системи
– ранг системи

![]()
і
![]() –
ранг системи рівнянь, що входять до цієї
системи. Система
–
ранг системи рівнянь, що входять до цієї
системи. Система
![]() сумісна тоді і тільки тоді, коли в її
матриці існує такий відмінний від нуля
мінор ∆ r-ого
порядку, який містить
сумісна тоді і тільки тоді, коли в її
матриці існує такий відмінний від нуля
мінор ∆ r-ого
порядку, який містить
![]() рядків, складених із коефіцієнтів
рівнянь системи
рядків, складених із коефіцієнтів
рівнянь системи
![]() ,
всі супровідні його визначники цієї
системи, які відповідають її рівнянням,
рівні нулю; відношення
,
всі супровідні його визначники цієї
системи, які відповідають її рівнянням,
рівні нулю; відношення
![]() для всіх супровідних визначників
для всіх супровідних визначників
![]() ,
які відповідають її нерівностям,
невід’ємні.
,
які відповідають її нерівностям,
невід’ємні.
Якщо
в системі
![]() ,
коефіцієнти при невідомих і‑ого
стовпця,
,
коефіцієнти при невідомих і‑ого
стовпця,
![]() ,
мають однаковий знак, то дана система
сумісна. Надаючи невідомим
,
мають однаковий знак, то дана система
сумісна. Надаючи невідомим
![]() довільних значень, одержуємо систему:
довільних значень, одержуємо систему:
![]() ,
,
з
якої знаходимо наступну область значень
![]() :
:

Контрольні питання для самоперевірки
-
Означення наслідку системи нерівностей.
-
Сформулюйте теорему Мінковського.
-
Які ви знаєте критерії сумісності системи лінійних нерівностей.
-
Сформулюйте критерії несумісності системи лінійних нерівностей Александрова, Чернікова.
-
Для яких систем нерівностей стверджується критерій Вороного? Сформулюйте цей критерій.
-
В чому полягає критерій Кронекера‑Капеллі?
-
Дослідити на сумісність наступні системи нерівностей:
а) б)
б)
 в)
в)

Література:
-
Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел, ч. ІІ – К.: Вища шк., 1980. – 402 с., гл. І, §2.
-
С.Г. Колесник, В. В. Цыбуленко. Алгебра и теория чисел, ч. ІІ. – Х., ХГПИ, 1992. – гл. ІV, §2.
Лекція 8 Тема: Системи лінійних нерівностей План:
-
Розв’язання системи лінійних нерівностей методом послідовного виключення невідомих.
-
Невід’ємні розв’язки системи лінійних рівнянь:
а) базисні розв’язки системи;
б) зв’язок між невід’ємними базисними розв’язками системи з невід’ємними розв’язками системи лінійних нерівностей;
в) зв’язок між невід’ємними розв’язками системи лінійних рівнянь з сумісністю відповідної системи однорідних нерівностей.
Короткий зміст лекції:
Нехай
![]() ,
,![]() –
система m
лінійних нерівностей з n
невідомими. Позначимо її через S.
–
система m
лінійних нерівностей з n
невідомими. Позначимо її через S.
-
Якщо в системі S коефіцієнти при невідомих i-ого стовпця,
 мають однаковий знак, то система сумісна;
для будь-якого
мають однаковий знак, то система сумісна;
для будь-якого
 ,
надаючи невідомим
,
надаючи невідомим
 довільних значень, знаходимо область
значень
довільних значень, знаходимо область
значень
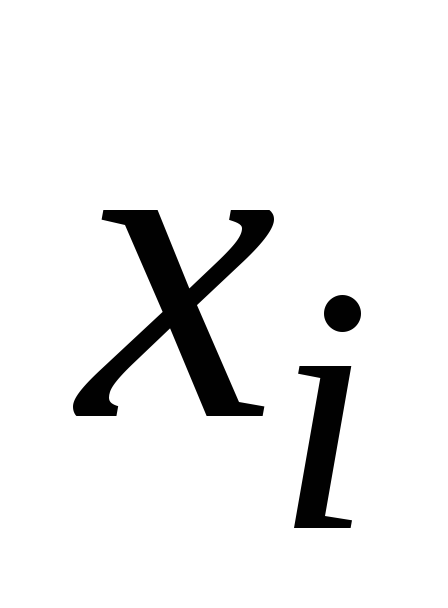 .
. -
Нехай
 –
будь-яка нерівність системи S.
–
будь-яка нерівність системи S.
Якщо
![]() ,
то залишаємо цю нерівність без змін.
,
то залишаємо цю нерівність без змін.
Якщо
![]() ,
то переносимо член
,
то переносимо член
![]() в праву частину і ділимо обидві частини
нерівності на додатне число –
в праву частину і ділимо обидві частини
нерівності на додатне число –
![]() ,
одержуємо нерівність виду:
,
одержуємо нерівність виду:
![]() .
.
Якщо
![]() ,
то переносимо в праву частину нерівності
всі доданки, крім
,
то переносимо в праву частину нерівності
всі доданки, крім
![]() ,
і ділимо обидві частини нерівності на
,
і ділимо обидві частини нерівності на
![]() ,
одержуємо нерівність
,
одержуємо нерівність
![]()
Помноживши кожну із нерівностей заданої системи на певне додатне число, одержуємо рівносильну до неї систему виду:

![]()
де
![]() –
вирази виду
–
вирази виду
![]() ,
які не містять
,
які не містять
![]() .
.
Тоді система

яка
не містить
![]() ,
називається супровідною
відносно даної системи S
або рівносильної до неї системи Т.
,
називається супровідною
відносно даної системи S
або рівносильної до неї системи Т.
Між
системами S
і
![]() існує зв’язок, який виражається теоремою:
існує зв’язок, який виражається теоремою:
Якщо
від будь-якого розв’язку системи S
відкинути значення останнього невідомого
![]() ,
то одержимо деякий розв’язок супровідної
системи S.
,
то одержимо деякий розв’язок супровідної
системи S.
Доведення.
Перше
твердження теореми очевидне (якщо деякий
набір значень невідомих задовольняє
системі S,
то він задовольняє і системі Т,
але тоді для цього ж набору виконуються
і всі нерівності системи
![]() ).
).
Доведемо друге твердження
Нехай
![]() – будь-який розв’язок системи
– будь-який розв’язок системи
![]() .
Підставивши вказані значення невідомих
у вирази
.
Підставивши вказані значення невідомих
у вирази
![]() ,
одержимо деякі числа
,
одержимо деякі числа
![]() .
Для них повинні виконуватись нерівності
.
Для них повинні виконуватись нерівності
![]() .
.
Ці
нерівності показують, що кожне з чисел
![]() не більше будь-якого з чисел
не більше будь-якого з чисел
![]() .
Але в такому випадку обов’язково
знайдеться число
.
Але в такому випадку обов’язково
знайдеться число
![]() ,
яке задовольняє нерівності
,
яке задовольняє нерівності
![]() ,
але ці нерівності разом з нерівностями
,
але ці нерівності разом з нерівностями
![]() означають, що набір значень невідомих
означають, що набір значень невідомих
![]() є розв’язком системи Т,
а отже, і системи S.
є розв’язком системи Т,
а отже, і системи S.
Теорему доведено.
Важливу роль відіграють наступні додатки до теореми:
-
Система S лінійних нерівностей сумісна тоді і тільки тоді, коли сумісна супровідна до неї система
 .
Це – прямий наслідок доведеної теореми.
.
Це – прямий наслідок доведеної теореми. -
Всі розв’язки даної системи S можна одержати наступним способом: треба до кожного розв’язку
 супровідної системи
супровідної системи
 приєднати будь-яке з чисел
приєднати будь-яке з чисел
 ,
що знаходиться між усіма числами
,
що знаходиться між усіма числами
 і всіма числами
і всіма числами
 .
.
Отже,
для довільної системи S
лінійних нерівностей з невідомими
![]() ми побудували нову супровідну систему
ми побудували нову супровідну систему
![]() ,
в якій невідомими є
,
в якій невідомими є
![]() .
.
Але
для системи
![]() можна, в свою чергу, побудувати супровідну
систему
можна, в свою чергу, побудувати супровідну
систему
![]() (з невідомими
(з невідомими
![]() )
для останньої – супровідну систему
)
для останньої – супровідну систему
![]() і т.д.
і т.д.
Продовжуючи
цей процес, ми після ряду кроків прийдемо
до системи
![]() ,
яка складається з нерівностей з одним
невідомим
,
яка складається з нерівностей з одним
невідомим
![]() .
.
З
вказаного вище твердження 1 випливає,
що система S
сумісна тоді і тільки тоді, коли сумісна
система
![]() .
.
Отже, за допомогою простих обчислень вирішується питання про сумісність системи S.
Припустимо, що система S сумісна. Як знайти всі її розв’язки?
Система
S
розв’язана, якщо побудовані системи
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Означення.
Набір значень перших k
невідомих
![]() називається допустимим,
якщо його можна продовжити до розв’язку
заданої системи S,
тобто якщо існують такі числа
називається допустимим,
якщо його можна продовжити до розв’язку
заданої системи S,
тобто якщо існують такі числа
![]() ,
що набір
,
що набір
![]() є розв’язком системи S.
є розв’язком системи S.
Як
тільки побудовані системи
![]() ,
,
![]() ,
…,
,
…,
![]() ,
ми одержуємо можливість:
,
ми одержуємо можливість:
-
знайти всі допустимі значення невідомого
 із системи
із системи
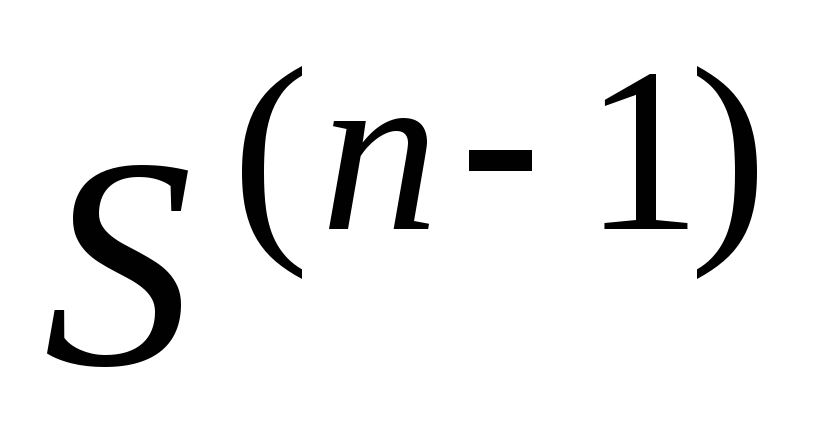 ;
; -
для будь-якого конкретного допустимого значення
 знайти всі сумісні з ним значення
невідомого
знайти всі сумісні з ним значення
невідомого
 ,
тобто такі значення , які разом з
,
тобто такі значення , які разом з
 утворюють допустимий набір (вони
знаходяться шляхом підстановки
утворюють допустимий набір (вони
знаходяться шляхом підстановки
 в систему
в систему
 );
); -
для будь-якого конкретного допустимого набору
 ,
,
 знайти всі сумісні з ним значення
невідомого
знайти всі сумісні з ним значення
невідомого
 (вони знаходяться шляхом підстановки
(вони знаходяться шляхом підстановки
 ,
,
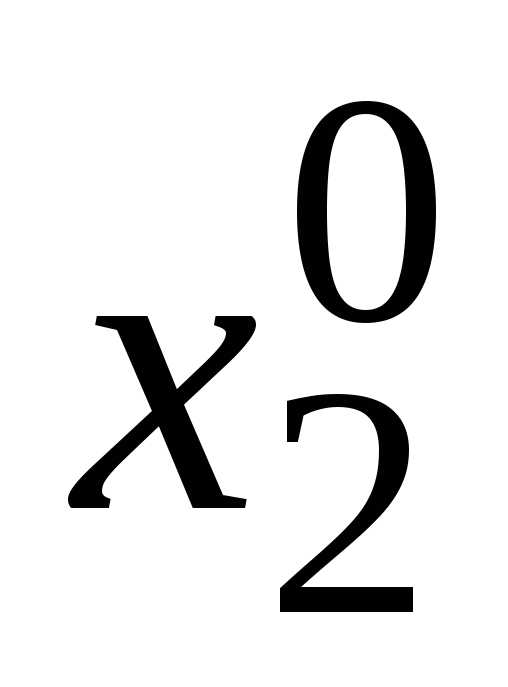 в систему
в систему
 )
і т.д.
)
і т.д.
Отже,
саме так треба розуміти наше твердження,
що система S
розв’язана, якщо побудовані системи
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Розглянемо питання про невід’ємні розв’язки системи лінійних рівнянь.
Нехай
|
|
(1) |
є
сумісна система лінійних рівнянь рангу
![]() .
Стовпці матриці цієї системи будемо
розглядати як вектори простору
.
Стовпці матриці цієї системи будемо
розглядати як вектори простору
![]() :
:

Серед
стовпців
![]() виділимо базис. Нехай це будуть вектори
виділимо базис. Нехай це будуть вектори
![]() .
Невідомим із системи рівнянь, які не
відповідають стовпцям виділеного
базису, надамо значень, рівних нулю,
тобто
.
Невідомим із системи рівнянь, які не
відповідають стовпцям виділеного
базису, надамо значень, рівних нулю,
тобто
![]() .
.
Одержуємо систему з r невідомими рангу r, що має єдиний розв’язок.
Для
виділеного базису
![]() існує єдиний розв’язок системи (1)
існує єдиний розв’язок системи (1)
![]() ,
де
,
де
![]() при
при
![]() .
Цей розв’язок називається базисним.
.
Цей розв’язок називається базисним.
Система
(1) має стільки базисних розв’язків,
скільки різних базисів можна вибрати
в системі векторів
![]() .
.
Стверджуються наступні теореми:
-
Якщо система лінійних рівнянь
 має невід’ємні розв’язки, то вона має
також невід’ємні базисні розв’язки.
Щоб встановити, чи існує невід’ємний
розв’язок даної системи лінійних
рівнянь, достатньо знайти базисні
розв’язки системи (кількість їх
скінчена) і встановити, чи існують серед
них невід’ємні розв’язки. Якщо серед
базисних розв’язків системи лінійних
рівнянь немає жодного невід’ємного,
то система немає жодного невід’ємного
розв’язку.
має невід’ємні розв’язки, то вона має
також невід’ємні базисні розв’язки.
Щоб встановити, чи існує невід’ємний
розв’язок даної системи лінійних
рівнянь, достатньо знайти базисні
розв’язки системи (кількість їх
скінчена) і встановити, чи існують серед
них невід’ємні розв’язки. Якщо серед
базисних розв’язків системи лінійних
рівнянь немає жодного невід’ємного,
то система немає жодного невід’ємного
розв’язку. -
Система лінійних рівнянь
 ,
має невід’ємні розв’язки тоді і тільки
тоді, коли несумісна система лінійних
нерівностей:
,
має невід’ємні розв’язки тоді і тільки
тоді, коли несумісна система лінійних
нерівностей:

Контрольні питання для самоперевірки:
-
В чому полягає метод послідовного виключення невідомих розв’язування системи лінійних рівнянь?
-
Як побудувати супровідну систему до заданої системи лінійних нерівностей?
-
Який зв’язок існує між сумісністю заданої системи та супровідної до неї системи?
-
Який набір значень невідомих називається допустимими?
-
Як знайти розв’язки сумісної системи лінійних нерівностей за допомогою методу послідовного виключення невідомих?
-
Який розв’язок називається базисним розв’язком системи лінійних рівнянь?
-
Який розв’язок називається невід’ємним? Додатнім?
-
Теорема про існування невід’ємного розв’язку системи лінійних рівнянь.
-
Який зв’язок між існуванням невід’ємного розв’язку системи лінійних рівнянь з несумісністю відповідної системи однорідних лінійних нерівностей?
-
Методом послідовного виключення невідомих розв’язати системи нерівностей:
а) б)
б)

-
З’ясувати, чи мають системи рівнянь невід’ємні розв’язки:
а)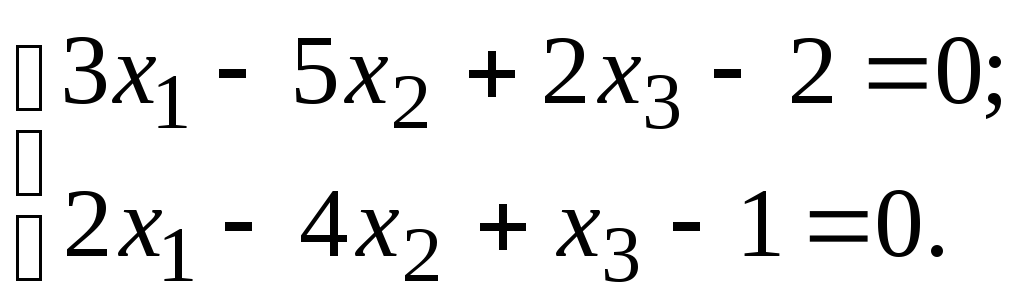 б)
б)

(розв’язати вправи двома способами).
Література:
-
Солодовников А.С. Системы линейных неравенств. – М.: Наука, 1977.
-
С.Г. Колесник, В. В. Цыбуленко. Алгебра и теория чисел, ч. І. – Х, 1992. – 255 с.
