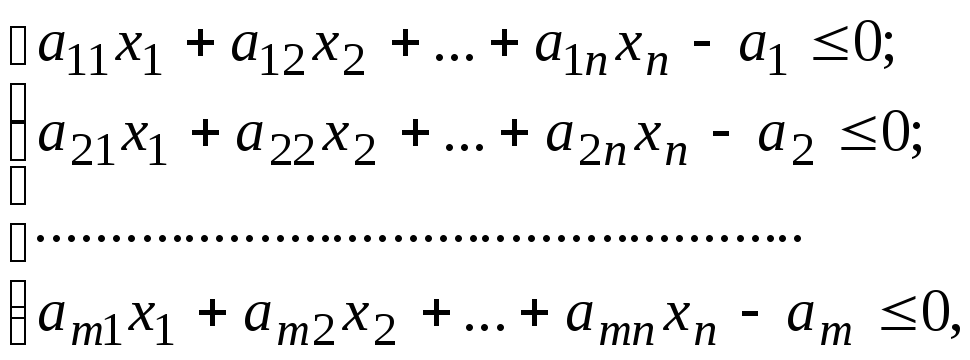Лекція 6 Тема: Системи лінійних нерівностей

План:

1. Означення системи лінійних нерівностей.

2. Однорідні системи нерівностей.

3. Геометричний зміст системи.

4. Розв’язок системи лінійних нерівностей.

5. Поняття опуклої множини, півпростору, многогранника розв’язків.

6. Сумісні системи нерівностей. Ранг системи.

7. Зв’язок між системою лінійних нерівностей і системою лінійних рівнянь.

Короткий зміст лекції:

Нехай R – поле дійсних чисел, – арифметичний n-вимірний векторний простір.

називається лінійною формою над простором . Лінійна форма , якщо всі ; , якщо хоча б одне із .

Сукупність елементів , що задовольняє рівнянню

,

називається площиною простору . Співвідношення називається лінійною нерівністю.

Множина елементів з , яка задовольняє нерівності називається півпростором, який визначається площиною

Нехай – елементи з . Сукупність елементів з , які визначаються формулою називається відрізком в просторі , що з’єднує .

Півпростір є опуклою множиною, тобто поряд з будь-якими своїми елементами містить і весь відрізок, що їх сполучає. Будь-яку опуклу множину можна одержати як перетин всіх півпросторів, які мають з даною множиною спільну точку.

Опуклим многогранником простору називається непустий перетин скінченої кількістю півпросторів. Многогранник є опуклою множиною і алгебраїчно визначається системою нерівностей:

(1)

де кожній нерівності , відповідає півпростір в , а їх перетин утворює многогранник, тобто многогранник – це множина елементів простору , що задовольняє системі (1).

Будь-яка система нерівностей виду (1) називається системою m лінійних нерівностей з n невідомими, числа – коефіцієнти при невідомих; – вільні члени.

Якщо ,, то система (1) називається однорідною.

Набір дійсних чисел , який задовольняє кожній нерівності системи (1), називається розв’язком системи нерівностей.

Якщо всі , розв’язок називається невід’ємним.

Система лінійних нерівностей (1) сумісна (розв’язна), якщо вона має хоч би один розв’язок, у противному випадку несумісна (нерозв’язна).

Дві системи лінійних нерівностей називаються рівносильними, якщо множини їх розв’язків співпадають.

Рангом системи лінійних нерівностей називається максимальна кількість лінійно незалежних в ній лінійних форм.

Ранг системи лінійних нерівностей дорівнює рангу матриці цієї системи.

Якщо система (1) сумісна і множина її розв’язків відмінна від , то ця множина називається многогранником розв’язків системи, або просто многогранником.

Між системами лінійних нерівностей та лінійних рівнянь можна встановити наступне співвідношення. Будь-якій системі m лінійних нерівностей з n невідомими

(2)

поставимо у відповідність систему m лінійних рівнянь з n + m невідомими:

(3)

Тоді справедлива наступна теорема:

Якщо є розв’язком системи лінійних рівнянь (3) і , , то є розв’язком системи лінійних нерівностей (2).

Зв’язок між системою лінійних нерівностей і відповідною системою лінійних рівнянь дозволяє визначити сумісність системи лінійних нерівностей (2), і у випадку сумісності знайти мінімальну кількість нерівностей, яка визначає многогранник її розв’язків.

Розв’язати систему лінійних нерівностей означає:

а) дослідити її на сумісність;

б) у випадку сумісності знайти многогранник її розв’язків.

Контрольні питання для самоперевірки:

1. Дайте означення лінійної форми від n невідомих, лінійної нерівності.

2. Що розуміють під площиною простору ?

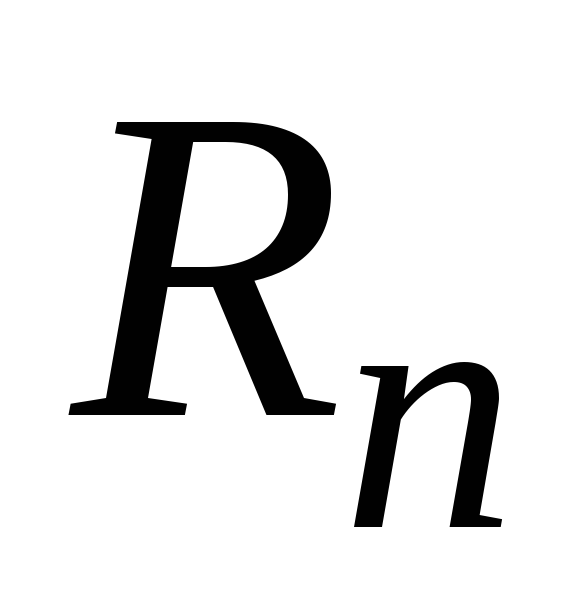3. Дайте означення півпростору; чим визначається півпростір?

4. Що розуміють під відрізком в просторі ?

5. Дайте означення опуклої множини; опуклого многогранника?

6. Як алгебраїчно виражається многогранник?

7. Дайте означення системи лінійних нерівностей.

8. Який геометричний зміст системи лінійних нерівностей з двома невідомими?

9. Який геометричний зміст системи лінійних нерівностей з n невідомими?

10. Який існує зв’язок між системою m лінійних нерівностей з n невідомими і відповідними системами лінійних рівнянь?

11. Що означає розв’язати систему лінійних нерівностей?

12. Що називається рангом системи лінійних нерівностей?

13. Користуючись теоремою про зв’язок між системою лінійних нерівностей з відповідною системою лінійних рівнянь, розв’язати системи нерівностей:

а) б)

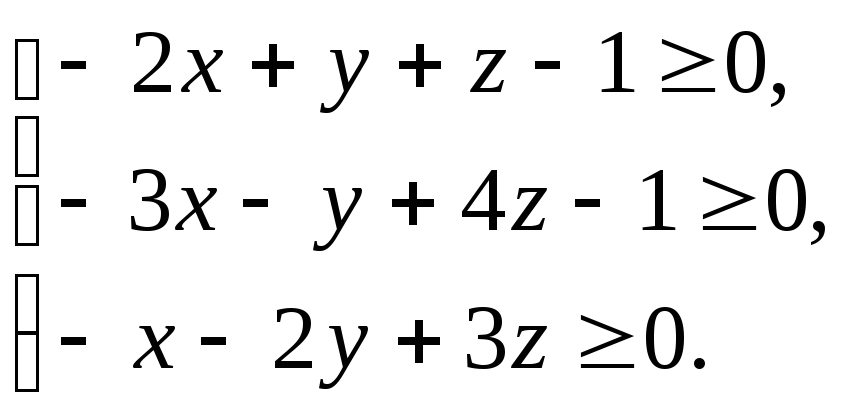
14. Знайти область розв’язків систем лінійних нерівностей:

а)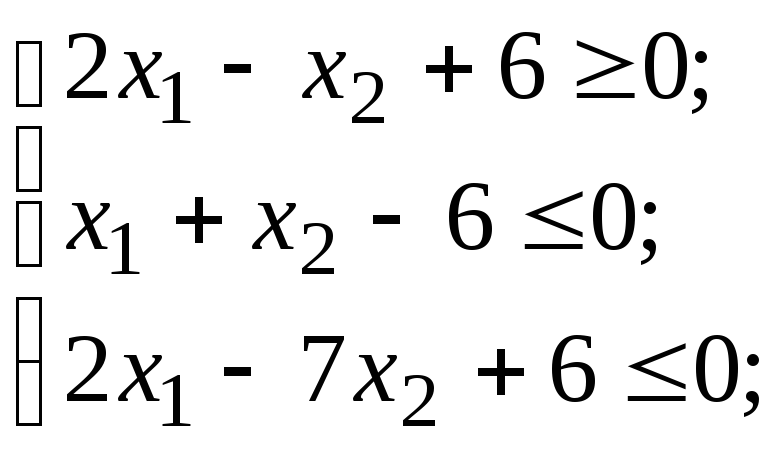 б)

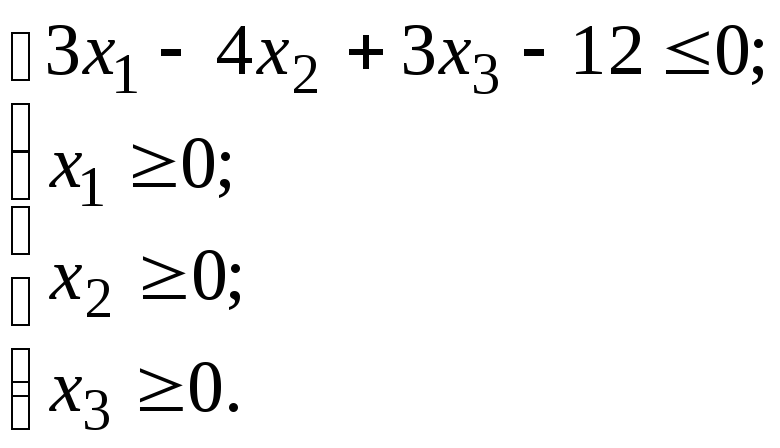
15. Доведіть, що область розв’язків М будь-якої системи лінійних нерівностей є опуклою множиною.

Література:

1. Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел, ч. ІІ – К.: Вища шк., 1980. – 402 с., гл. І, §1.

2. С.Г. Колесник. Алгебра. – Х., ХГПИ, 1992. – Гл. V, §1.