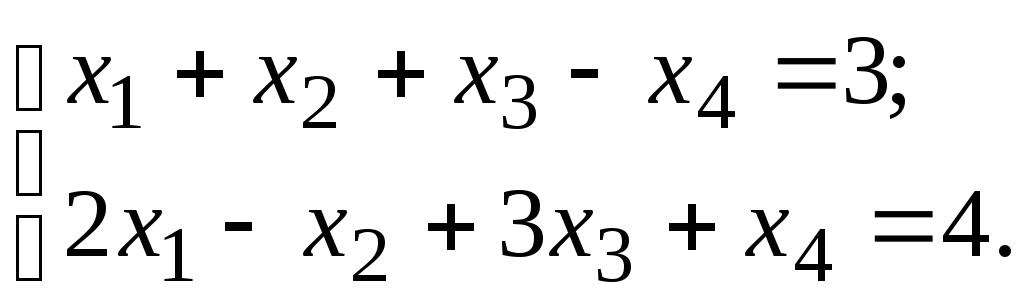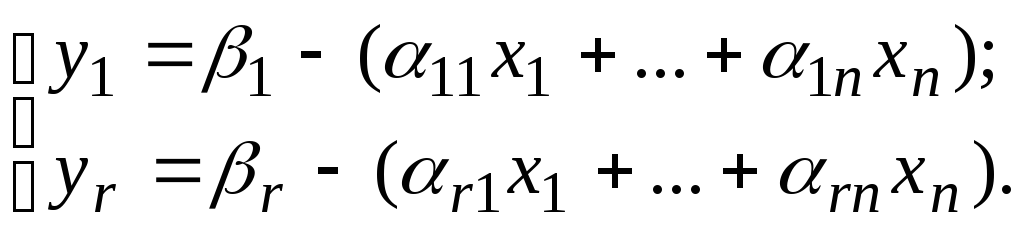Контрольні питання для самоперевірки:

1. Сформулюйте канонічну задачу лінійного програмування.

2. В чому полягає суть симплекс-методу розв’язування задачі лінійного програмування?

3. Сформулюйте порядок роботи за симплекс-методом.

4. Як складаються симплекс-таблиці та в чому полягає операція заміщення вектора базису?

5. На множині невід’ємних розв’язків системи лінійних рівнянь

знайти такий, який мінізував би цільову функцію .

6. На множині невід’ємних розв’язків системи лінійних нерівностей

знайти такий, який мінімізує цільову функцію .

Література:

1. С.Т.Завало, В.М.Костарчук, Б.І.Хацет. Алгебра і теорія чисел, Ч.2. – К.: Вища школа, 1980. – Гл.І, 3,4,5.

2. Колесник С.Г., Цыбуленко В.В.. Алгебра и теория чисел, Ч.І – Х.: ХГПУ, 1998. – Гл. 5, 2.2.

Лекція 14 Тема: Знаходження невід’ємних розв’язків системи лінійних рівнянь симплекс-методом План:

1. Застосування канонічної задачі мінімізації для знаходження невід’ємних розв’язків системи лінійних рівнянь.

2. Відшукання першого базису канонічної задачі.

Короткий зміст лекції:

При вивченні симплекс-методу ми припускаємо, що нам відомий допустимий базисний розв’язок канонічної задачі мінімізації, тобто невід’ємний базисний розв’язок системи обмежень цієї задачі. Але розв’язування кожної канонічної задачі симплекс-методом починається саме з відшукання невід’ємного базисного розв’язку її системи обмежень, тобто системи рівнянь виду:

.

(1)

Тому треба з’ясувати, як знайти невід’ємний базисний розв’язок системи (1).

Звичайно, можна було б спробувати знайти всі базисні розв’язки системи (1), вважаючи, що на певному етапі знайдемо і невід’ємний базисний розв’язок. Але доцільніше розв’язати цю задачу зведенням її до канонічної задачі мінімізації.

Будемо вважати, що в системі (1) всі вільні члени невід’ємні, тобто, (цього завжди можна досягти, помноживши кожне рівняння системи (1), в якого вільний член від’ємний, на –1).

Розглянемо наступну канонічну задачу мінімізації: знайти невід’ємний вектор , який задовольняє системі обмежень та мінімізує функцію:

.

(2)

Назвемо цю задачу І. Доведемо, що система рівнянь(1) має невід’ємний розв’язок тоді і тільки тоді, коли значення задачі І дорівнює нулю.

Доведення.

Якщо система (1) має невід’ємний розв’язок , то задача І має допустимий розв’язок: .

Значення цільової функції при дорівнює нулю. Для будь-якого іншого допустимого розв’язку задачі І значення цільової функції (2) не менше, ніж нуль. Тому є оптимальним розв’язком задачі І, і її значення .

Обернено, якщо – оптимальний розв’язок задачі І, , то, враховуючи співвідношення (2), і, отже, є невід’ємним розв’язком системи (1).

Отже, якщо – оптимальний розв’язок задачі І і значення , то є невід’ємним розв’язком системи (1); якщо ж значення задачі І не дорівнює нулю, то система (1) невід’ємних розв’язків не має.

Розглянемо приклад.

Для заданої системи лінійних рівнянь:

(1)

за допомогою канонічної задачі та симплекс-методу з’ясувати, чи має вона невід’ємний розв’язок; якщо має, то знайти його.

Розв’язання.

Будуємо систему рівнянь:

(*)

та цільову функцію .

Одержуємо канонічну задачу мінімізації функції f на множині невід’ємних розв’язків системи (*).

Система рівнянь (1) має невід’ємний розв’язок, якщо на множині невід’ємних розв’язків системи (*) існує оптимальний розв‘язок системи (1). Симплекс-методом знайдемо оптимальний розв’язок поставленої задачі. Ранг системи рівнянь (*) дорівнює 2. Отже, система має чотири вільних невідомих. Нехай це будуть .

Виражаємо базисні невідомі і функцію через вільні невідомі, одержуємо систему.

Складаємо таблицю 1.

Таблиця 1

Базисні невідомі							Вільні члени
	1	0		0
	0	1		–1
f	0	0	0	0	–1	–1	0

З таблиці 1 знаходимо оптимальний розв’язок канонічної задачі . Значення канонічної задачі . Отже, є невід’ємним розв’язком заданої системи лінійних рівнянь.

В багатьох задачах лінійного програмування базис убачається безпосередньо. В інших задачах його треба шукати.

Розглянемо один з методів відшукання базису – метод штучного базису.

Нехай система обмежень задана у загальному виді:

(1)

Числа можна вважати невід’ємними, якщо це не так, наприклад, якщо , то, помноживши обидві частини першого рівняння на –1, одержимо рівняння, в якому вільний член буде більше нуля. Отже, нехай . Введемо допоміжні, або штучні невідомі , пов’язані з рівняннями:

(2)

Очевидно, що розв’язування системи (1) рівносильне розв’язуванню системи (2) при додаткових умовах .

В системі (2) штучні невідомі утворюють базис. Припустимо, що нам вдалося, відправляючись від цього базису, перейти до іншого базису, в якому немає жодного штучного невідомого, наприклад, до базису . Інакше, припустимо, що після даних перетворень система (2) зводиться до виду:

(3)

Надаючи нульових значень, одержуємо систему:

(4)

яка рівносильна заданій системі (1). Але в системі (4) невідомі утворюють базис; отже, задача знаходження базису розв’язана.

Залишається вирішити, як від системи (2) перейти до системи (3). Застосуємо симплекс-метод. Симплекс-методом будемо розв’язувати задачу мінімізації форми при обмеженнях (2), а також при умовах: .

Умови, при яких починає діяти симплекс-метод, тут виконані, оскільки система (2) має належний вид (виділено базис). Після декількох кроків буде одержано шуканий мінімум.

Оскільки, то і min, тому можливі два випадки:

1. min F > 0. Це означає, що система (2) не має невід’ємних розв’язків, для яких (в протилежному випадку min F = 0). Отже, задана система (1) також немає невід’ємних розв’язків. Звідси випливає, що будь-яка задача лінійного програмування з системою обмежень (1) не має розв’язків.

2. min F = 0. З останньої симплекс-таблиці знаходимо оптимальній розв’язок: . Оскільки , то . Звідси випливає, що – невід’ємний розв’язок даної системи (1).

Отже, у випадку min F = 0 дана система (1) має хоча б один невід’ємний розв’язок.

Далі, якщо з останньої симплекс-таблиці дістанемо, що штучні невідомі знаходяться серед небазисних, то ми досягли (3), а, отже, і (4), відкидаючи з останньої таблиці стовпці , а також останній рядок (для форми F), приходимо до першої симплекс-таблиці для системи (4), тобто по суті для даної системи (1).

Залишається доповнити одержану таблицю рядком для форми f, яку треба мінімізувати в заданій задачі, і перша симплекс-таблиця готова.

Примітка: Може статися, що серед невідомих заданої системи (1) є таке, наприклад,, яке входить тільки в одне рівняння системи, нехай в перше, причому коефіцієнт при цьому невідомому має такий же знак, що і вільний член. Тоді немає необхідності вводити для першого рівняння штучне невідоме. Достатньо представити рівняння у вигляді:

де , і розглядати як перше невідоме базису.

Розглянемо приклад.

Задана система рівнянь:

та лінійна форма . Серед невід’ємних розв’язків даної системи вибрати такий, який мінімізує форму.

Розв’язання.

Знайдемо з першого рівняння:

і оголошуємо одним з базисних невідомих.

Для інших двох рівнянь вводимо штучні невідомі i . Одержуємо систему:

За допомогою симплекс-методу мінімізуємо форму .

Перша симплекс-таблиця має вигляд.

Таблиця 1

	Базисні невідомі								Вільні члени
		3	-5	1	2	0	0	0	1
		-2	2	0	-1	1	1	0	4
		-1	3	0	-2	1	0	1	5
	F	-3	5	0	-3	2	0	0	9
	f	-1	-2	0	0	0	0	0	0

У результаті першого кроку невідоме виходить з базису. Наступні кроки мають на меті мінімізувати форму F. Переходимо до таблиці 2, викреслюючи стовпчик .

Таблиця 2

	Базисні невідомі							Вільні члени
		3	-5	1	2	0	0	1
		-2	2	0	-1	1	0	4
		1	1	0	-1	0	1	1
	F	1	1	0	-1	0	0	1
	f	-1	-2	0	0	0	0	0

Розв’язувальний елемент 1 обираємо в рядку і стовпці . Отже, після другого кроку обидва штучних невідомих стають небазисними. Цей факт свідчить про те, що min F = 0 (оскільки в останньому базисному розв’язку == 0). Відкидаємо стовпчик , а також рядок F і переходимо до таблиці 3.

Таблиця 3

	Базисні невідомі						Вільні члени
		8	0	1	–3	0	6
		– 4	0	0	1	1	2
		1	1	0	–1	0	1
	f	1	0	0	–2	0	2

Отже, в заданій системі обмежень виділено базис .

Таблицю 3 можна розглянути як першу симплекс-таблицю заданої задачі.

Розв’язувальний елемент 8 обираємо в рядку і стовпці . Переходимо до таблиці 4.

Таблиця 4

Базисні невідомі						Вільні члени
	1	0	1	–3	0
	0	0	0	0	1	5
	0	1	0	0	0
f	1	0	0	2	0

Звідси видно, що форма f досягає мінімуму, . Оптимальний розв’язок є .

Якщо в процесі мінімізації форми F ми прийшли до такої таблиці, в якій штучні невідомі вже знаходяться серед небазисних, то це свідчить про те, що мінімум F досягнуто, і він дорівнює нулю. Дійсно, в останньому базисному розв’язку , отже, і F = 0.

Тому, переходячи до наступної таблиці, відкидаємо не тільки стовпчик для останнього штучного невідомого, але і рядок для F. Одержана так таблиця розглядається як перша симплекс-таблиця для поставленої задачі.

Контрольні питання для самоперевірки:

1. Як знайти невід’ємний базисний розв’язок канонічної задачі мінімізації?

2. В чому полягає «метод штучного базису» відшукання базису системи-обмежень канонічної задачі?

3. За допомогою симплекс-методу з’ясувати, чи мають системи рівнянь невід’ємний розв’язок та знайти будь-який з них:

а) б)

4. Серед невід’ємних розв’язків системи рівнянь:

знайти такий, що мінімізує функцію .

Література:

1. С.Т.Завало, В.М.Костарчук, Б.І.Хацет. Алгебра і теорія чисел, Ч.2. – К.: Вища школа, 1980. – Гл.І, §4.4.

2. Колесник С.Г., Цыбуленко В.В.. Алгебра и теория чисел, Ч.І – Х.: ХГПУ, 1996. – Гл. 5,§ 22.

3. Солодовников А.С. Введение в линейную алгебру и линейное программирование. – М.: Просвещение, 1966. – Гл. 6,§ 26.