§2. Понятие координатной системы

В математике рассматриваются различные множества и пространства. Среди них предпочтение отдается числовым множествам и арифметическим пространствам различной размерности, так как в таких пространствах отношения между элементами выражаются через операции сложения и умножения чисел. Если для не числового пространства удается установить взаимно однозначное соответствие с элементами арифметического пространства определенной размерности, то отношения связывающие элементы не числового пространства можно также описать с помощью операций сложения и умножения чисел, что очень удобно.

Итак, пусть нам дано непустое множество М, элементы которого условно назовем точками, n-мерное арифметическое пространство Rⁿ и некоторые подмножества Ω и Λ в них соответственно, т.е. Ω М, Λ Rⁿ.

Определение 2.1. Всякое взаимно однозначное отображение f множества Ω на множество Λ называется n-мерной координатной системой на множестве М, а множество Ω координатной окрестностью этой координатной системы.

Число п называется размерностью координатной системы и оно совпадает с показателем размерности арифметического пространства Аⁿ, в котором находится множество Λ.

Пусть точка М принадлежит множеству Ω и пусть f (М) = (m₁, m₂, …, m_n), где (m₁, m₂, …, m_n) элемент из множества Λ. В этом случае числа m₁, m₂, …, m_n называются координатами точки М в данной координатной системе f и записывают М(m₁, m₂, …, m_n).

Для задания координатной системы на исходном множестве М выбирают конечную упорядоченную систему элементов или, как мы их назвали, упорядоченную систему точек. Она должна быть такой, чтобы с ее помощью, используя существующие на множестве М отношения между его элементами, можно было задать координатную систему. Эта система точек называется репером.

Выбор репера зависит от математической структуры, которая задана на данном множестве. Например, в векторном пространстве его элементы – векторы могут быть линейно зависимыми или нет. Если в таком пространстве, например, существует упорядоченная система из п линейно независимых векторов , обладающая тем свойством, что она становится линейно зависимой при добавлении к этой системе еще одного вектора , то такую систему называют базисом. В этом случае вектор может быть представлен единственным образом в виде линейной комбинации с некоторыми числовыми коэффициентами

= х₁ + … + х_п .

Таким образом, всякому вектору ставится в соответствие упорядоченный набор чисел (х₁, …, х_п) и обратно. Следовательно, построенное отображение является координатной системой, векторы образуют базис, а коэффициенты разложения вектора по базису являются координатами вектора в данном базисе.

Также легко задается координатная система в точечном евклидовом 3-мерном пространстве. Для этого достаточно взять точку, например, О и три линейно независимых вектора , , и отложить их от точки О. В результате появятся еще три точки, например, Х₁, Х₂, Х₃. Фигуру R, состоящую из точек О, Х₁, Х₂, Х₃ взятых в указанном порядке, можно обозначить иначе - R = {О, , , }. В этом случае для произвольной точки М будем иметь

= m₁ + m₂ +m₃ .

Тройку чисел (m₁, m₂, m₃) называют декартовыми координатами точки М.

Следует заметить, что построение координатной системы задача не простая. Бывают структуры, в которых координатная система задается достаточно сложно. Например, в проективных пространствах. Поскольку проективное пространство Рⁿ порождается векторным пространством размерности п+1, то для построения системы координат в Рⁿ можно воспользоваться координатной системой соответствующего векторного пространства. Рассмотрим, например, проективную прямую. Пусть проективная прямая Р¹ порождена векторным пространством и пусть базис этого пространства состоит из векторов и . Будем считать, что

= + (2.1)

Векторы порождают на проективной прямой соответственно точки Х₁(), Х₂(), Х₀(). Тогда, в силу условия (2.1), эти точки согласованы между собой, то есть Х₀ = Х₁+ Х₂. Упорядоченную тройку точек Х₁, Х_2, Х₀, где Х₀ = Х₁+ Х₂, называют проективным репером на прямой.

Пусть точка М() принадлежит проективной прямой. Тогда векторы, порождающие точки М, Х₁ и Х₂, будут линейно зависимыми, то есть

= m₁ + m_{2 .}

Данное условие запишем при помощи точек, порождаемых этими векторами, в виде

М = m₁ Х₁ + m₂ Х₂.

Согласно определению проективного пространства точка М порождается не только вектором , но также вектором r. Таким образом, точке М необходимо поставить в соответствие числовые пары вида (rm₁ , rm₂), где r - произвольный скалярный множитель отличный от нуля. В результате возникает взаимно однозначное соответствие между множеством точек проективной прямой и множеством таких пар. Пару чисел (rm₁, rm₂) называют однородными проективными координатами точки М в проективном репере R = {Х₁, Х_2, Х₀} и записывают М(rm₁, rm₂) или М(m₁: m₂). Эти записи означают, что при вычислительных операциях можно использовать либо пару чисел m₁ , m₂, либо пару пропорциональную данной.

Из определения координатной системы следует, что на одном и том же множестве может быть много координатных систем, среди которых есть так называемые «удобные » координатные системы. Заметим, что понятие «удобная координатная система» зависит от той задачи, которая рассматривается на данном множестве. В такой системе решение задачи выглядит наиболее просто. В этой связи часто возникает необходимость перехода от данной системы к другой, например «удобной». Пусть на множестве М заданы две координатные системы, например, f₁ и f₂ реперами R₁ и R₂ соответственно. Координаты произвольной точки М из множества М в этих координатных системах обозначим соответственно (, , …, ) и (, ,…, ). Рассмотрим композицию ◦ = f. Тогда, ◦ = (М) = (, , …, ). Таким образом, отображение f элементы (, ,…, ) множества Rⁿ взаимно однозначно отображает на элементы (, , …, ) этого же множества, т.е. f (, , …, ) = (, , …, ), и называется оно преобразованием координат (рис. 2.1).

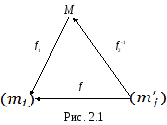
Если координатные системы f₁ и f₂ задаются соответственно реперами R и R¢, то в этом случае говорят, что осуществлен переход от репера R¢ к реперу R. При этом координаты данной точки М относительно этих реперов будут связаны между собой некоторыми зависимостями, порождаемых отображением f:

= (, , …, ),

= (, , …, ), (2.2)

……….

= (, , …, ).

Так как реперы R и находятся в одном множестве, то элементы одного репера обладают вполне определенными координатами относительно другого репера и эти координаты обязаны входить в функции . В классических однородных пространствах простейшие геометрические объекты задаются уравнениями первой степени. При замене координатной системы объект не должен менять своих свойств, то есть должен сохраняться порядок уравнения его задающего. Отсюда, функции должны носить линейный характер и обеспечивать возможность выражения координат через координаты , так как отображение f , их порождающее, является биекцией. То есть эти функции должны иметь вид

= (), i = 1,…, п. (2.3)

При этом коэффициенты a_ij образуют матрицу c определителем отличным от нуля.

Таким образом, если на множестве выбрана какая либо координатная система f, то все координатные системы на этом множестве можно разбить на два класса К₁ и К₂. К классу К₁ отнесем саму систему f и все те переход от которых к системе f осуществляется согласно (2.3) при условии  0. К классу К₂ отнесем все остальные, т.е. те для которых  0.

Если на множестве из классов К₁ и К₂ выбран один, то говорят, что на данном множестве задана ориентация. Таким образом, на множестве возможны только две ориентации. Одну из них называют провой ориентацией (или положительной), тогда другую, соответственно, левой (отрицательной).

В качестве примера, найдем соотношения (2.2) в случае n-мерного векторного пространства, поскольку это пространство наиболее часто участвует в построении других математических структур. Пусть в даны два базиса В = (, … , ) и базис В¢=(,…, ). В n-мерном векторном пространстве всякие n+1 вектора линейно зависимы. Следовательно, векторы базиса В¢ есть линейные комбинации базисных векторов базиса В, т.е.

= +…+ ,

………. (2.4)

= +…+ ,

В формулах 2.4 матрицу называют матрицей перехода от базиса В к базису В¢. Заметим, ранг этой матрицы равен п (в силу линейной независимости базисных векторов).

Возьмем произвольный вектор и пусть его координаты относительно базиса В будут (, , …, ), а относительно базиса В¢ соответственно - (, , …, ). Тогда, по определению координат вектора, будем иметь

= +…+ (2.5)

= +…+ . (2.6)

Разложения (2.4) подставим в правую часть равенства (2.6) и сравним полученный результат с правой частью равенства (2.5). В силу линейной независимости базисных векторов получим:

= + … + ,

= + … + , (2.7)

……….

= + … + .

Коэффициенты в равенствах 2.7 образуют матрицу транспонированную к матрице . В силу линейной независимости векторов , определитель матрицы не равен нулю. Матрицу называют матрицей перехода от координатной системы задаваемой базисом В¢, к координатной системе задаваемой базисом В или, допуская вольность речи, матрицей перехода от базиса В¢ к базису В.

Таким образом, функции (2.2) в п-мерном векторном пространстве имеют вид (2.7). В других пространствах функции (2.2) будут иметь другой вид.