3. 5. Комплексные числа

В предыдущем пункте мы получили фундаментальный результат, состоящий в установлении непрерывности действительной оси, т.е. это означает, что никаких других чисел на действительной оси не существует. Однако множество не замкнуто относительно операции извлечения корня. В частности, уравнение типа мы по-прежнему не умеем решать. Р. Декарт (1637 г.) предложил искать новые числа, на множестве которых станет возможным решение подобных задач на плоскости, т.е. рассматривать их как координаты точек в ДПСК-2. При этом число представляется как упорядоченная пара двух действительных чисел, где пара . Для пар вида должны выполняться все операции над действительными числами (принцип перманентности). Оказалось, это возможно сделать, если дать следующее определение.

Определение 1. Комплексным числом называется упорядоченная пара действительных чисел такая, что выполняются следующие условия. Пусть и , тогда:

1. ;

2. ;

3. .

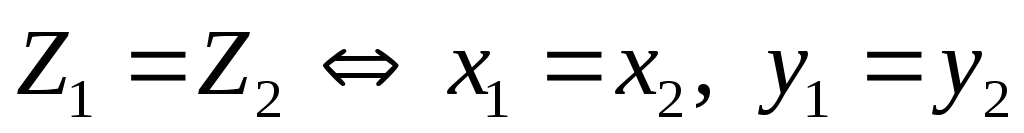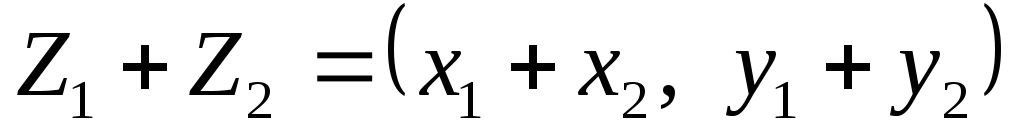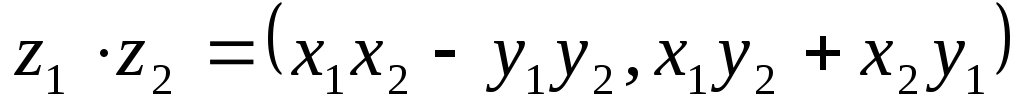Число (первый элемент пары) называется действительной частью числа , а (второй элемент пары) – мнимой частью. Обозначим их через , .

Операции над комплексными числами обладают свойствами ассоциативности, коммутативности и дистрибутивности (показать).

Положим . Числа , удовлетворяют всем правилам операций над действительными числами (показать).

Рассмотрим число и возведём его в квадрат: . Таким образом, число является решением уравнения . Это число Р. Декарт назвал мнимой единицей и обозначил .

3. 5. 1. Алгебраическая форма комплексного числа

Запись комплексного числа в виде не совсем удобна при выполнении арифметических операций над комплексными числами. Поэтому перейдем к алгебраической форме записи комплексного числа. Пусть . Рассмотрим число и умножим его на :

, т.е. .

Используя введённые обозначения , , , получим: . Такое представление называют алгебраической формой комплексного числа .

Определение 2. Число называется комплексно сопряжённым числу . Отметим, что , .

Арифметические действия над комплексными числами , выполняются по следующим формулам:

1. ;

2. ;

3. , .

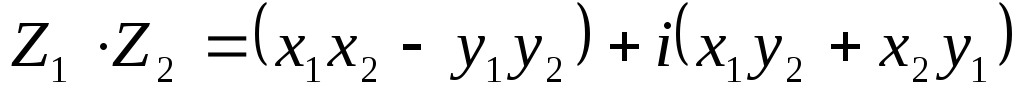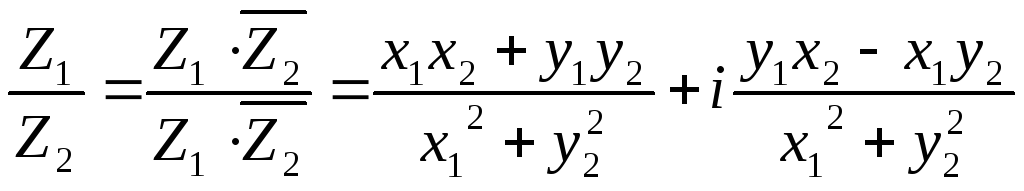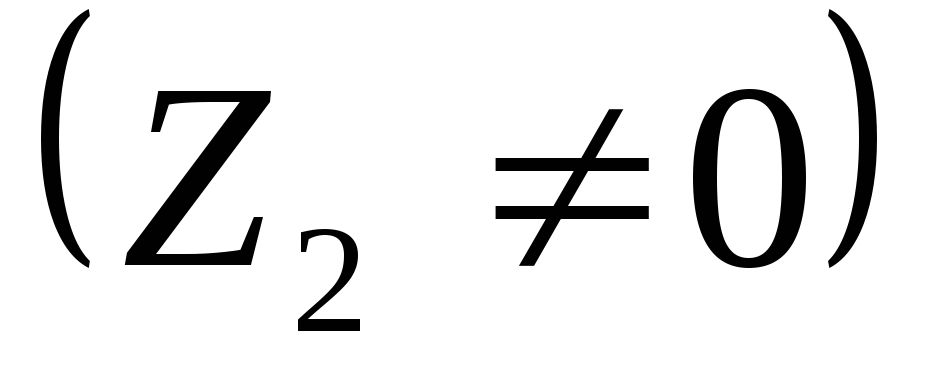Пример. Пусть , . Найти , , .

,

,

. ■

3.5. 2. Геометрическая интерпретация комплексного числа

В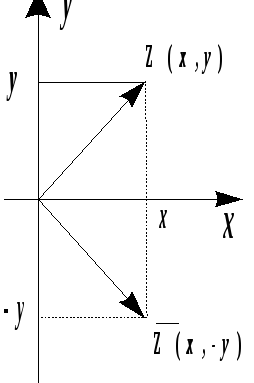 соответствии с идеей Декарта, каждому комплексному числу можно сопоставить точку на плоскости или её радиус-вектор. Можно показать, что между множеством комплексных чисел и множеством радиус-векторов точек плоскости существует взаимно однозначное соответствие. Таким образом, комплексно сопряжённые числа и изображаются точками, симметричными относительно оси . Заметим, что комплексные числа складываются и вычитаются по правилу сложения векторов.

Определение 1. Длина радиус-вектора, соответствующего числа , называется модулем этого числа и .

Определение 2. Аргументом комплексного числа называется угол между соответствующим радиус-вектором и положительным направлением оси .

Отметим, что , если отсчет ведет против часовой стрелки, и , если – по часовой стрелке. Для числа понятие аргумента не вводится, а при , определяется с точностью до слагаемого , . Среди всех значений , , существует только одно значение, лежащее в промежутке (или ). Оно называется главным и обозначается . Следовательно, .