
- •Глава II Векторная алгебра
- •П. 1 Понятие вектора. Линейные операции
- •Определение 2. Вектор (Гиббс) – математический объект, характеризуемый скалярной величиной, направлением и геометрическим характером сложения.
- •Пример. В одномерном случае преобразование пространства – это биекция, у которой ,.
- •П. 2 Базис на плоскости
- •Доказательство:
- •П. 4 Линейная независимость векторов
- •П. 7 Скалярное произведение векторов
- •Свойства скалярного произведения:
- •Дистрибутивность: .
- •Решение:
- •П. 8 Скалярное произведение в дпск
- •Наличие обратной операции
- •П. 9 Орт вектора. Направляющие косинусы вектора
- •П. 10 Векторное произведение векторов
- •Свойства векторного произведения:
- •Антикоммутативность: .
- •Дистрибутивность:
- •Векторное произведение в дпск
- •Решение:
- •П. 11 Произведения тройки векторов п. 11.1 Смешанное произведение векторов
- •Свойства смешанного произведения
- •Доказательство:
- •П. 12 Основные задачи векторной алгебры
- •П. 12.1 Плоскость в пространстве
- •Основные задачи
- •Угол между двумя плоскостями.
- •Расстояние от точки до плоскости.
- •П. 12.2 Прямая на плоскости
- •Другие уравнения прямой:
- •Угол между двумя прямыми
- •Условие перпендикулярности:
- •Условие параллельности:
- •Расстояние от точки до прямой
- •П. 12.3 Прямая в пространстве
- •Угол между прямыми
- •П.13 Линии второго порядка п.13.1 Эллипс
- •Свойства эллипса
- •Доказательство:
- •П. 13.2 Гипербола
- •Свойства гиперболы
- •П. 13.3 о гиперболических функциях
- •П. 13.4 Парабола
- •Свойства параболы
- •П.14 Поверхности второго порядка п. 14.1 Поверхности вращения
- •П. 14.2 Поверхности второго порядка
- •3. Двуполостной гиперболоид:
- •Цилиндрические поверхности
- •9. Гиперболический параболоид
П. 7 Скалярное произведение векторов
Определение 1.
Скалярным произведением векторов
![]() и
и
![]() называется операция (результат операции),
ставящая в соответствии упорядоченной
паре векторов
называется операция (результат операции),
ставящая в соответствии упорядоченной
паре векторов
![]() и
и
![]() скаляр,
равный произведению длин векторов на
косинус угла между ними.
скаляр,
равный произведению длин векторов на
косинус угла между ними.
![]() .
.
Замечание.
Из определения
скалярного произведения, следует, что
![]() .
.
Замечание.
Заметим, что
![]() .
Если взять вектор
.
Если взять вектор
![]() такой, что
такой, что
![]() ,
то
,
то
![]() .
Таким образом, скалярное произведение
одного вектора на другой, имеющий
единичную длину, равно проекции первого
вектора на направление, определяемое
вторым. В этом заключается геометрический
смысл
скалярного произведения.
.
Таким образом, скалярное произведение
одного вектора на другой, имеющий
единичную длину, равно проекции первого
вектора на направление, определяемое
вторым. В этом заключается геометрический
смысл
скалярного произведения.
Замечание.
Механический смысл скалярного
произведения.
Если рассмотреть действия силы
![]() на
материальную точку при её перемещении
по вектору
на
материальную точку при её перемещении
по вектору
![]() ,
то работа
,
то работа
![]() ,
совершаемая этой силой равна:
,
совершаемая этой силой равна:
![]() .
.
Свойства скалярного произведения:
-
Коммутативность:
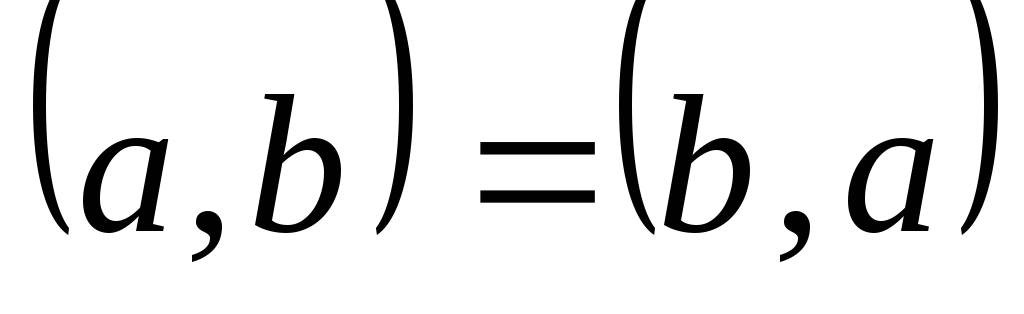 .
.
Доказательство:
![]() .
■
.
■
-
Унитарность:
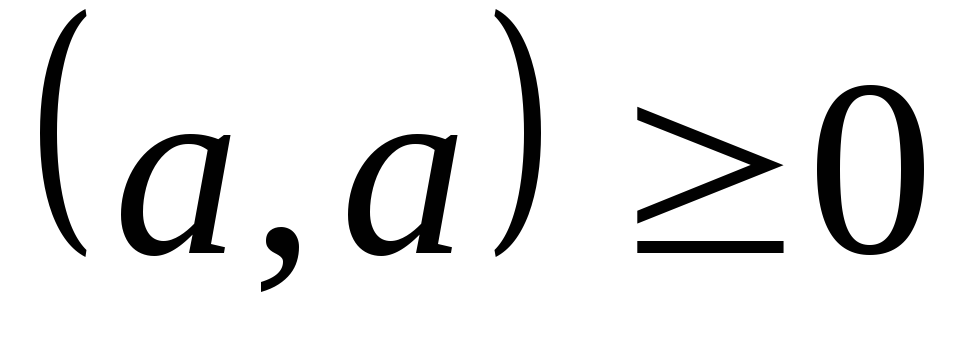 ,
причём
,
причём
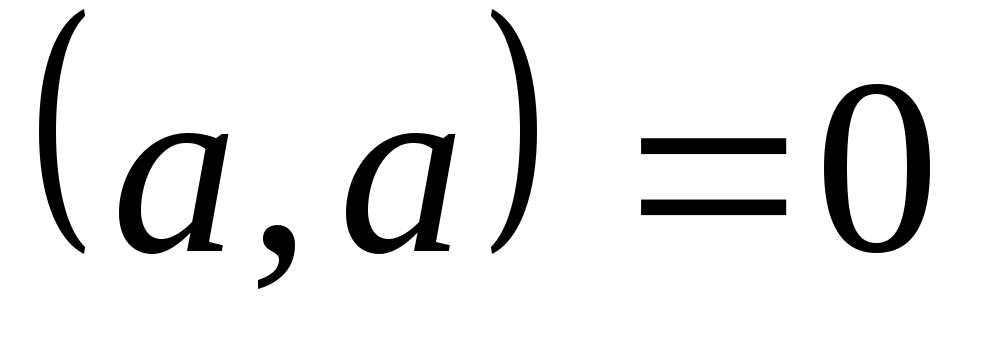 тогда и только тогда, когда
тогда и только тогда, когда
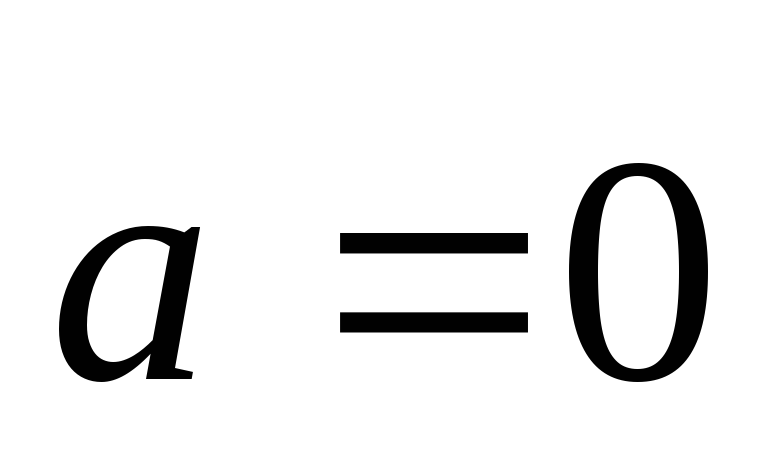 .
.
Доказательство:
![]() .
■
.
■
-
Однородность:
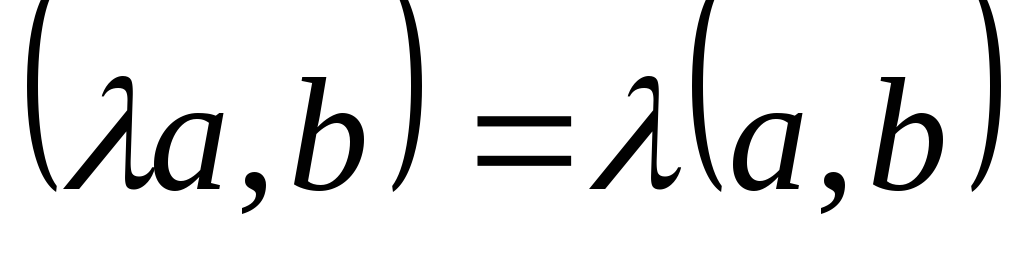 .
.
Доказательство:
![]() .
■
.
■
-
Дистрибутивность: .
Доказательство:
![]()
![]() .
■
.
■
Замечание. « однородность + дистрибутивность = линейность».
Теорема1. Критерий ортогональности
Пусть
векторы
![]() и
и
![]() .
Тогда
.
Тогда
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
.
Пример.
В треугольнике
![]() медиана
медиана
![]() перпендикулярна биссектрис
перпендикулярна биссектрис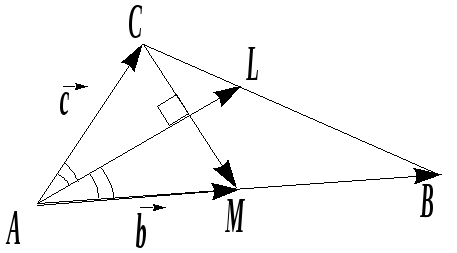 е
е![]() ,
причём
,
причём
![]() .
Найти угол
.
Найти угол![]() .
.
Решение:
Обозначим
![]() ,
,
![]() ,
,
![]()
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
Выразим
.
Выразим
![]() .
.
Известно,
что биссектриса угла делит противолежащую
сторону в отношении, равном отношении
длин прилежащих сторон. Таким образом,
![]() .
По условию,
.
По условию,
![]() ,
т.е.
,
т.е.
![]()
![]() .
.
Так
как
![]() ,
,
![]() ,
то
,
то
![]() .
(В этом можно было убедиться и геометрически:
по условию задачи, в
.
(В этом можно было убедиться и геометрически:
по условию задачи, в
![]() биссектриса
биссектриса
![]() является и высотой, а значит,
является и высотой, а значит,
![]() –
равнобедренный, т.е.
–
равнобедренный, т.е.
![]() ).
).
Таким
образом,![]()
![]()
![]() ,
,![]()
![]() .
Следовательно,
.
Следовательно,
![]() .
Отсюда находим
.
Отсюда находим
![]() .
.
П. 8 Скалярное произведение в дпск
Рассмотрим
векторы
![]() и
и
![]() в ДПСК
в ДПСК
![]() .
Из определения скалярного произведения
для базисных векторов имеем:
.
Из определения скалярного произведения
для базисных векторов имеем:
![]() ,
,
![]() или
или
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
0 |
1 |
0 |
|
|
0 |
0 |
1 |
Тогда
![]()
![]()
![]() .
.
Итак,
![]() .
Заметим, что
.
Заметим, что
![]() .
Тогда
.
Тогда
![]() ,
а также
,
а также
![]() .
.
Наличие обратной операции
П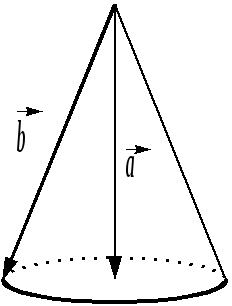 усть
даны вектор
усть
даны вектор
![]() и скалярное произведение
и скалярное произведение
![]() .
Можно ли найти вектор
.
Можно ли найти вектор
![]() ?
?
Как
было показано,
![]() .
Все векторы
.
Все векторы
![]() лежат
на конусе, осью которого является
носитель вектор
лежат
на конусе, осью которого является
носитель вектор
![]() (прямая, на которой лежит вектор), т.е.
таких векторов
(прямая, на которой лежит вектор), т.е.
таких векторов
![]() бесконечно много.
бесконечно много.
Таким образом, обратная операция не определена.
П. 9 Орт вектора. Направляющие косинусы вектора
О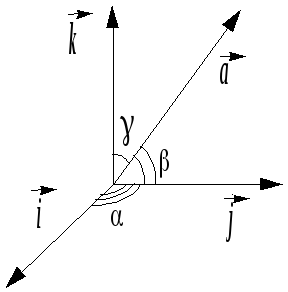 пределение 1.
Косинусы углов, которые вектор
пределение 1.
Косинусы углов, которые вектор
![]() образует с базисными
образует с базисными
![]() ,
,![]() ,
,![]() ,
называются направляющими
косинусами
вектора
,
называются направляющими
косинусами
вектора
![]() .
Обозначают
.
Обозначают
![]() ,
,
![]() ,
,
![]() .
.
Определение 2.
Ортом вектора
называется вектор
![]() ,
имеющий единичную длину и тоже направление,
что и вектор
,
имеющий единичную длину и тоже направление,
что и вектор
![]() :
:
![]() .
.
Покажем,
что координатами орта
![]() вектора
вектора
![]() являются его направляющие косинусы.
являются его направляющие косинусы.
Пусть
![]() .
Рассмотрим
.
Рассмотрим
![]() .
С другой стороны,
.
С другой стороны,
![]() .
Следовательно,
.
Следовательно,
![]() .
Аналогично можно показать, что
.
Аналогично можно показать, что
![]() ,
,
![]() .
Заметим, что
.
Заметим, что
![]() .
.
П. 10 Векторное произведение векторов
Определение
1.
Рассмотрим некоторую произвольную
тройку некомпланарных векторов
![]() ,
,![]() ,
,![]() ,
приведённых к точке
,
приведённых к точке
![]() .
Тройка векторов
.
Тройка векторов
![]() ,
,![]() ,
,![]() называется правой,
если для неё выполняется правило
буравчика: глядя с конца вектора
называется правой,
если для неё выполняется правило
буравчика: глядя с конца вектора
![]() и
и
![]() ,
можно увидеть, что кратчайший поворот
от
,
можно увидеть, что кратчайший поворот
от
![]() к
к
![]() происходит против часовой стрелки.
происходит против часовой стрелки.
Определение
2.
Векторным
произведением векторов
называется операция (рез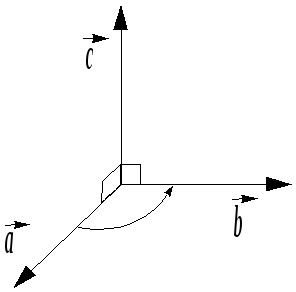 ультат
операции), которая любой упорядоченной
паре векторов
ультат
операции), которая любой упорядоченной
паре векторов
![]() и
и ![]() ставит в соответствие вектор
ставит в соответствие вектор
![]() ,
обладающий следующими свойствами:
,
обладающий следующими свойствами:
-
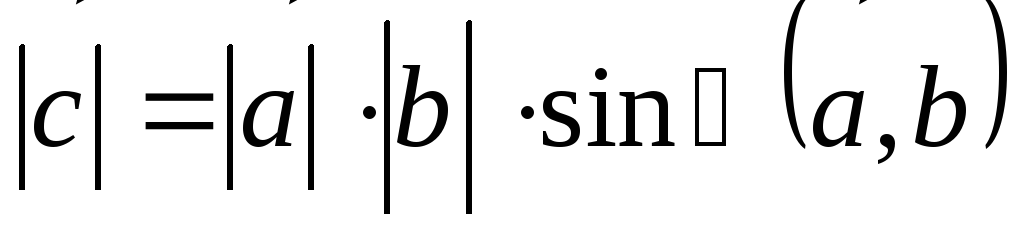 ;
;
2)
вектор
![]() ортогонален каждому
ортогонален каждому
из
![]() и
и
![]() ;
;
-
 ,
,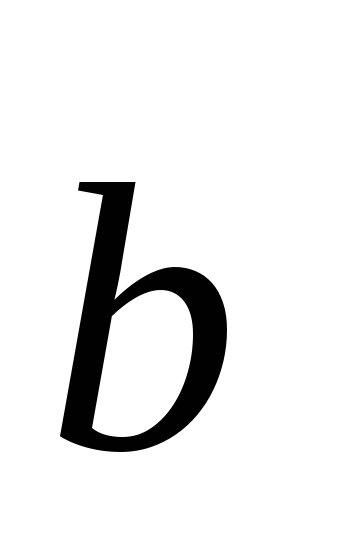 ,
, – правая тройка;
– правая тройка; -
если
 и
и
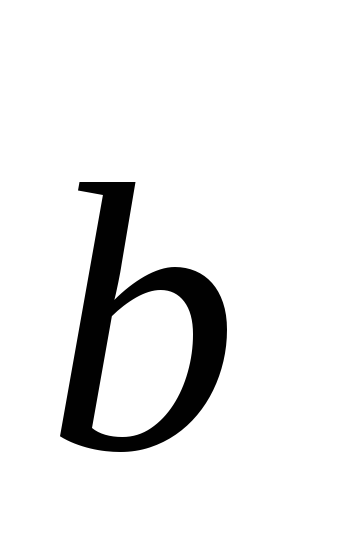 - коллинеарные, то
- коллинеарные, то
 =
= .
.
Замечание.
Геометрический смысл векторного
произведения
двух вектор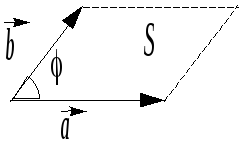 ов
ов
![]() и
и
![]() состоит в том, что модуль
состоит в том, что модуль
![]() равен площади
равен площади
![]() параллелограмма, построенного на
векторах
параллелограмма, построенного на
векторах
![]() и
и
![]() .
.
Замечание.
Механический смысл векторного
произведения.
Если вектор
![]()
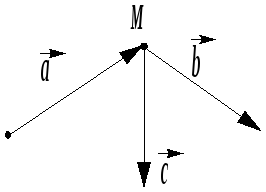 изображает приложенную в некоторой
точке М
силу, а вектор
изображает приложенную в некоторой
точке М
силу, а вектор
![]() идёт из некоторой
точки О
в точку
М,
то вектор
идёт из некоторой
точки О
в точку
М,
то вектор
![]() представляет собой момент силы
представляет собой момент силы
![]() относительно точки О.
относительно точки О.
