Основное уравнение термодинамики. Это уравнение объединяет формулы первого и второго начала термодинамики:

Q = dU + р dV, (3.9)

. (3.10)

Подставим уравнение (3.9), выражающее второе начало термодинамики, в равенство (3.10):

.

Это и есть основное уравнение термодинамики.

В заключение еще раз отметим, что если первый закон термодинамики содержит энергетический баланс процесса, то второй закон показывает его возможное направление.

Третье начало термодинамики

Ещё один закон термодинамики был установлен в процессе исследования изменения энтропии химических реакций в 1906 г. В. Нернстом. Он носит название теорема Нернста или третье начало термодинамики и связан с поведением теплоемкости веществ при абсолютном нуле температур.

Теорема Нернста утверждает, что при приближении к абсолютному нулю энтропия системы также стремится к нулю, независимо от того, какие значения принимают все остальные параметры состояния системы:

.

Поскольку энтропия 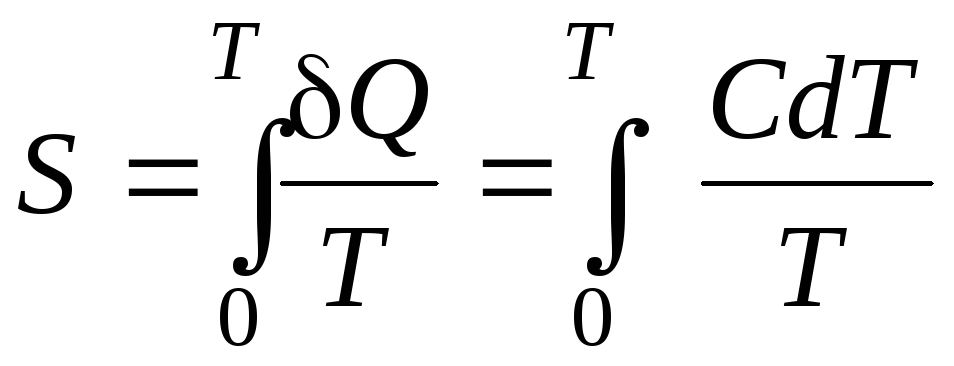, а температура Т стремится к нулю, теплоемкость вещества также должна стремиться к нулю, причем быстрее, чем Т. Отсюда следует недостижимость абсолютного нуля температуры при конечной последовательности термодинамических процессов, то есть конечного числа операций – циклов работы холодильной машины (вторая формулировка третьего начала термодинамики).

Реальные газы

Уравнение Ван-дер-Ваальса

Изменение состояния разреженных газов при достаточно высоких температурах и низких давлениях описывается законами идеального газа. Однако при увеличении давления и понижении температуры реального газа наблюдаются значительные отступления от этих законов, обусловленные существенными различиями между поведением реальных газов и поведением, которое приписывается частицам идеального газа.

Уравнение состояния реальных газов должно учитывать:

• конечное значение собственного объема молекул;

• взаимное притяжение молекул друг к другу.

Для этого Я. Ван-дер-Ваальс предложил включить в уравнение состояния не объем сосуда, как в уравнении Клапейрона-Менделеева (pV = RT), а объем моля газа, не занятый молекулами, то есть величину (V_  b), где V_ – молярный объем. Для учета сил притяжения между молекулами Я. Ван-дер-Ваальс ввел поправку к давлению, входящему в уравнение состояния.

Внося поправки, связанные с учетом собственного объема молекул (сил отталкивания) и сил притяжения в уравнение Клапейрона-Менделеева, получим уравнение состояния моля реального газа в виде:

.

Это уравнение Ван-дер-Ваальса, в котором постоянные а и b имеют разное значение для разных газов.

Лабораторная работа 9 Определение отношения теплоемкостей газов методом клемана - дезорма

Цель работы: определить отношение теплоемкостей газов (коэффициент Пуассона) методом Клемана – Дезорма.

Методика эксперимента

Общая схема установки представлена на рис. 3.7. Стеклянный баллон Б соединен с манометром М, измеряющим давление в сосуде. Изменение давления может осуществляться насосом Н, имеющим три рабочих положения, которые задействуются с помощью переключателя П.

У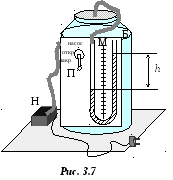становив переключатель П в положение насос, накачиваем воздух до некоторого давления, превышающего атмосферное. Через 1 – 2 минуты температура воздуха в баллоне становится равной температуре окружающей среды. Это состояние газа характеризуется давлением p₁, температурой Т₁ и удельным объёмом (V – объём баллона, m₁ – масса газа, находящегося в нем).

Давление p₁ определяется по формуле ,

где p₀ – атмосферное давление; p₁ – добавочное давление, измеряемое разностью уровней в манометре М.

Затем переводим переключатель в положение Открыто и как только уровни в манометре сравняются  в положение Закрыто. Выход воздуха происходит очень быстро и, пренебрегая в первом приближении передачей тепла через стенки сосуда, процесс расширения воздуха можно считать адиабатическим. В сосуде устанавливается давление p, равное атмосферному p₀. Газ имеет удельный объём (m₂ – масса газа, оставшегося в баллоне) и температуру Т₂.

Для адиабатического процесса справедливо уравнение Пуассона

или . (3.11) напомним, что V₁ и V₂ - объёмы единицы массы газа.

Через 1 – 2 минуты газ нагреется до температуры окружающей среды Т₂. Его давление в баллоне будет , где p₂ добавочное давление, измеряемое разностью уровней в манометре. удельный объём останется равным V₂, так как масса и объём газа не меняются. Сравнивая конечное состояние с начальным, видим, что температура в этих состояниях одинакова. Запишем для изотермического процесса закон Бойля-Мариотта

или . (3.12)

Решая ¹ систему уравнений (3.11) и (3.12), найдем :

.

Добавочные давления р₁ и р₂ определяются по формулам:

; , где   плотность воды, h₁ и h₂ – разность уровней воды в коленах манометра.

Окончательно получаем расчетную формулу для нашего опыта

. (3.13)

Таким образом, измеряя разности уровней воды в коленах манометра h₁ и h₂ , можно найти отношение теплоемкостей .

Примечание. При выполнении работы можно варьировать величину h₁, соответственно будет изменяться и h₂. Однако слишком большие значения h₁ брать нельзя, так как при этом в манометре возникают колебания столбика воды большой амплитуды.

Порядок выполнения работы

1. Включить насос в сеть 220 В.

2. Поставить переключатель П в положение Насос и накачать воздух в баллон Б до разности уровней воды в коленах манометра М приблизительно 8 – 10 см (см. примечание выше).

3. Перекрыть сообщение между баллоном Б и насосом Н, поставив переключатель П в положение Закрыто.

4. Подождать 2 – 3 минуты пока разность уровней воды в коленах манометра не перестанет меняться. Измерить h₁ (разность уровней воды в коленах манометра) по шкале линейки. Записать результат измерения в таблицу 3.1.

5. Поставить переключатель П в положение Открыто, как только уровни воды в коленах манометра сравняются, сразу перевести его в положение Закрыто.

6. Выждав 2 – 3 минуты (пока давление в манометре перестанет изменяться), снять отсчет h₂  установившейся разности уровней воды в коленах манометра. Записать результат измерения в таблицу 3.1.

7. Повторить пункты 2 – 6 пятикратно.

Таблица 3.1

h1	h2	i	теор	эксп	

Обработка результатов измерений

1. Рассчитать значения коэффициента Пуассона по формуле (3.13) для всех пяти измерений.

2. Вычислить теоретическое значение коэффициента Пуассона (_теор) по формуле .

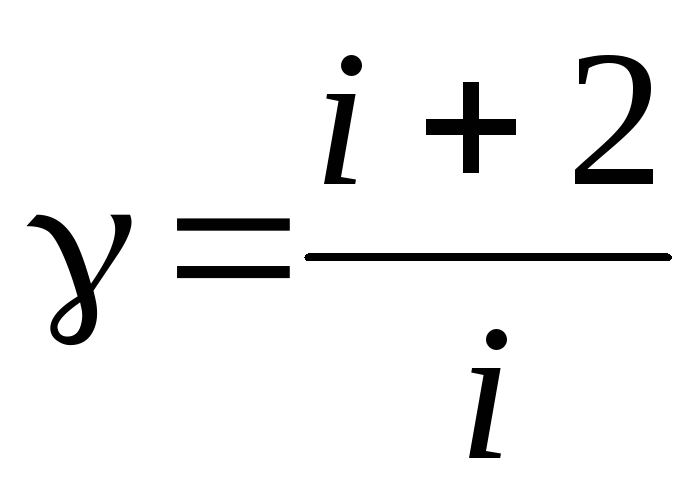3. В качестве результата эксперимента (_эксп) выбрать наиболее близкое к теоретическому значению из пяти, рассчитанных в п. 1.

4. Для _эксп рассчитать относительную погрешность по формуле .

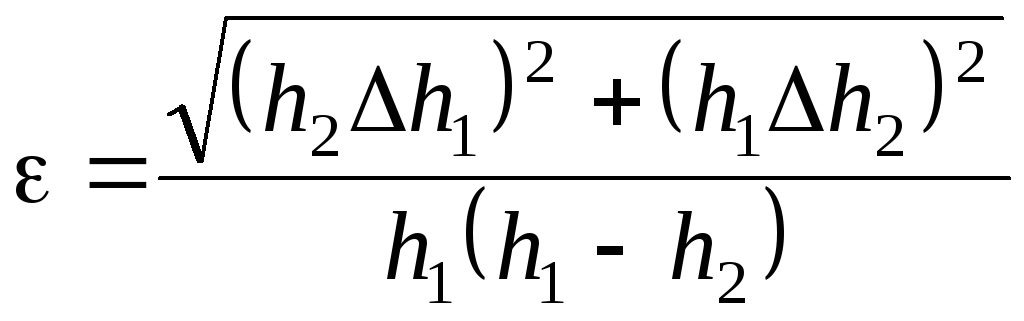5. Определить абсолютную погрешность по формуле  = _эксп.

6. Записать результат экспериментального определения коэффициента Пуассона  = (_эксп  )

7. Сделать вывод по проделанной работе.

Контрольные вопросы и задания

1. Сформулируйте первое начало термодинамики.

2. Как определяется внутренняя энергия системы? Запишите выражение для внутренней энергии идеального газа.

3. Что такое число степеней свободы? Как определяется это число для одно-, двух- и трехатомных молекул?

4. Что называется удельной и молярной теплоёмкостями?

5. Какие физические величины обозначаются знаками С_Р и С_V? Каким уравнением описывается связь между ними? Какие законы используются при выводе этого уравнения?

6. Какой процесс называется изотермическим? Изобарическим? Изохорическим? Адиабатическим? Запишите уравнения состояния для этих процессов.

7. Запишите первое начало термодинамики для всех изопроцессов и для адиабатического процесса.