Задачи с экономическим содержанием

Понятие матрицы часто используется в практической деятельности. Например, данные о выпуске продукции нескольких видов в каждом квартале года или нормы затрат нескольких видов ресурсов на производство продукции нескольких типов и т.д. удобно записывать в виде матриц.

Задача. Предприятие выпускает продукцию трёх видов: р₁, р₂, р₃ и использует сырьё двух типов: s₁ и s₂. Нормы расхода сырья характеризуются матрицей , где каждый элемент a_{i j} (i=1, 2, 3; j=1, 2) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой С=(100 80 130), стоимость единицы каждого типа сырья (ден.ед) ― матрицей-столбцом . Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.

► Затраты 1-го сырья составляют

ед.

и 2-го

ед.,

поэтому матрица-строка затрат сырья S может быть записана:

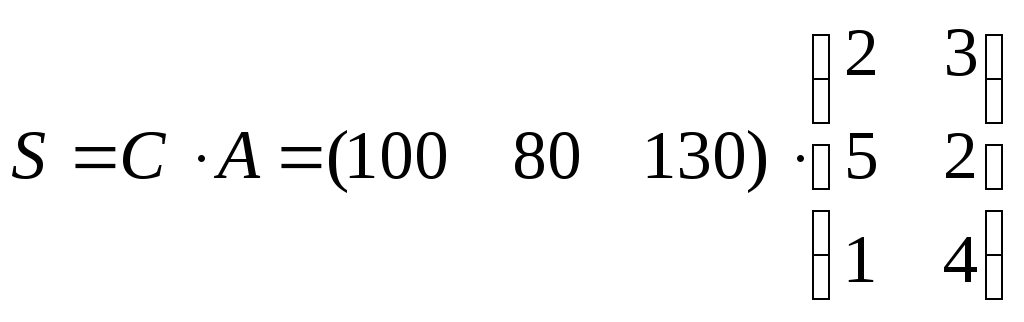=(730 980).

Тогда общая стоимость сырья

=70900 ден.ед. может быть записана в матричном виде:

=(70900).

Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу

,

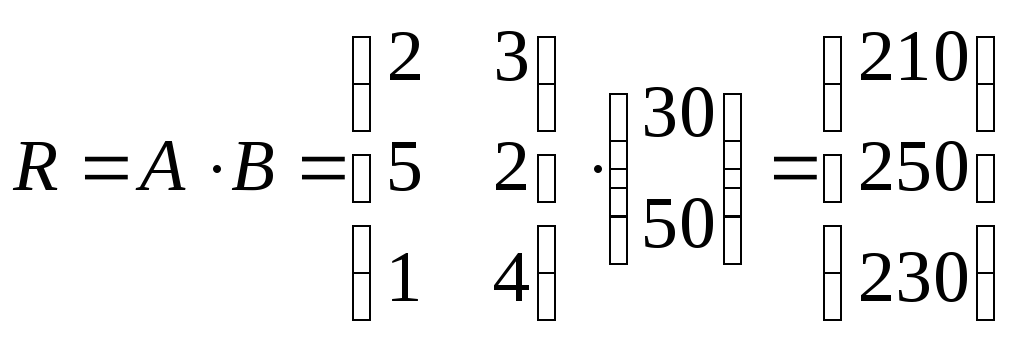а затем общую стоимость сырья

. ◄

№161. В некоторой отрасли m заводов выпускают n видов продукции. Матрица задаёт объёмы продукции на каждом заводе в первом квартале, матрица — соответственно во втором; — объёмы продукции j–го типа на i-м заводе в 1-м и 2-м квартале соответственно:

; .

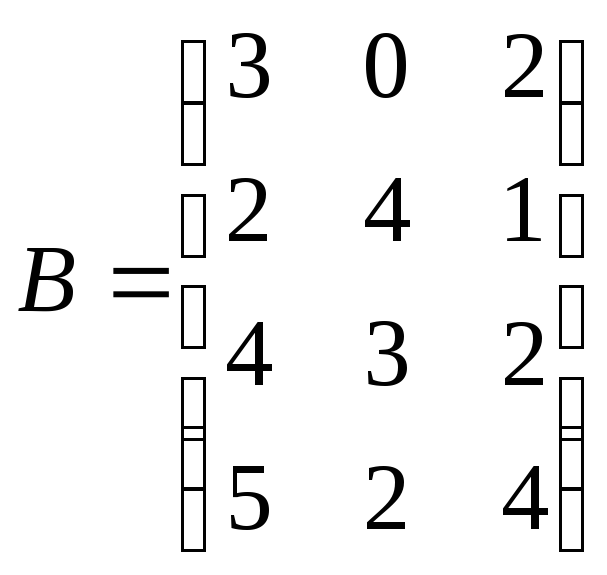Найти: а) объёмы продукции; б) прирост объёмов производства во втором квартале по сравнению с первым по видам продукции и заводам; в) стоимостное выражение выпущенной продукции за полгода (в долларах), если λ — курс доллара по отношению к рублю.

№162. Предприятие производит n типов продукции, объёмы выпуска заданны матрицей . Цена реализации единицы i-го типа продукции в j-м регионе задана матрицей , где k — число регионов, в которых реализуется продукция. Найти С — матрицу выручки по регионам.

№163. Предприятие производит n типов продукции, используя m видов ресурсов. Нормы затрат ресурса i-го товара на производство j-го типа задана матрицей затрат . Пусть за определённый отрезок времени предприятие выпустило количество продукции каждого типа x_{i j}, записанное матрицей . Определить S — матрицу полных затрат ресурсов каждого вида на производство всей продукции за данный период времени.

№164. Пусть в условии предыдущей задачи указана стоимость каждого вида ресурсов в расчёте на единицу, заданных матрицей Р=(10 20 10 10). Определить полную стоимость всех затраченных за данный отрезок времени ресурсов.

№165. Завод производит двигатели, которые могут быть либо сразу потребовать дополнительной регулировки (в 40% случаев), либо сразу могут быть использованы (в 60% случаев). Как показывают статистические исследования, те двигатели, которые изначально требовали регулировки. Требуют дополнительной регулировки через месяц в 65% случаев, а в 35% случаев через месяц будут работать хорошо. Те же двигатели, которые не требовали первоначальной регулировки, потребуют её через месяц в 20% случаев и продолжат хорошо работать в 80% случаев. Какова доля двигателей, которые будут работать хорошо или потребуют регулировки через 2 месяца после выпуска? Через 3 месяца?

№166. Три завода выпускают четыре вида продукции. Необходимо: а) найти матрицу выпуска продукции за квартал, если заданы матрицы месячных выпусков ; ; ; 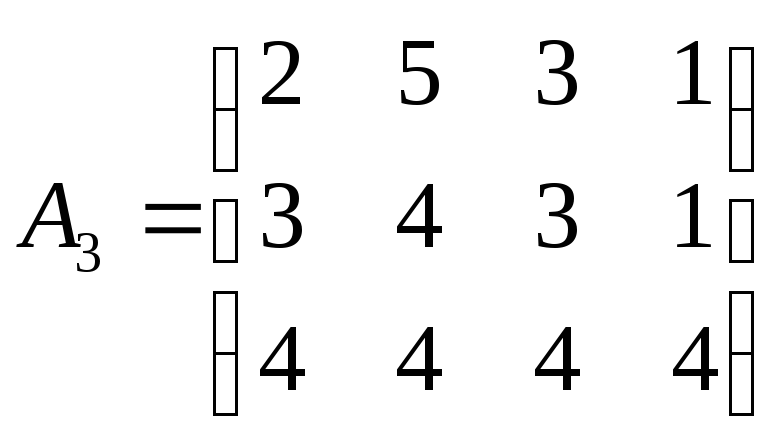найти матрицы приростов выпуска продукции за каждый месяц В₁ и В₂ и проанализировать результаты.

№167. Найти С — матрицу выручки по регионам в условиях задачи 162, если А=(10 40 10 20); .

Определить, какой из трёх регионов наиболее выгоден для реализации товара.

№168. Предприятие производит мебель трёх видов и продаёт её в четырёх регионах. Матрица задаёт цену реализации единицы мебели i-го типа j-м регионе. Определить выручку предприятия в каждом регионе, если реализация мебели за месяц (по видам) задана матрицей .

№169. В условиях задачи 163 и 164 определить:

1) полные затраты ресурсов 3-х видов на производство месячной продукции, если заданы нормы затрат матрицей и объём выпуска каждого из двух видов продукции ;

2) стоимость всех затраченных ресурсов, если задана стоимость единиц каждого ресурса Р=(50 10 20).

№170. Продавец может закупить от 1 до 5 билетов на спектакль по цене 100 руб. и продать перед спектаклем по 200 руб. каждый. Составить матрицу выручки продавца в зависимости от количества купленных им билетов (строка матрицы) и от результатов продажи (столбец матрицы).

№171. В ремонтную мастерскую поступают телефонные аппараты, 7% которых требуют малого ремонта, 20% — среднего ремонта, 10% — сложного ремонта. Статистически установлено, что 10% аппаратов, прошедших малый ремонт, через год требуют малого ремонта, 60% — среднего, 30% — сложного ремонта. Из аппаратов, прошедших средний ремонт. 20% требуют через год малого ремонта, 50% — среднего, 30% — сложного ремонта. Из аппаратов, прошедших сложный ремонт, через год 60% требуют малого ремонта, 40% — среднего. Найти доли из отремонтированных в начале года аппаратов, которые будут требовать ремонта того или иного вида: через 1 год; 2 года; 3 года.

№172. Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн. усл. ден. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго — на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: а) в минувшем году; б) в этом году?

№173. Фирмой было выделено 236 тыс. усл. ден. ед. для покупки 29 предметов для оборудования офиса: несколько компьютеров по цене 20 тыс. усл. ден. ед. за компьютер, офисных столов по 8, 5 тыс. усл. ден. ед. за стол, стульев по 1,5 тыс. усл. ден. ед. за стул. Позже выяснилось, что в другом месте компьютеры можно приобрести по 19,5 тыс. усл. ден. ед., а столы — по 8 тыс. усл. ден. ед. (стулья по той же цене), благодаря чему на туже сумму было куплено на 1 стол больше. Выяснить, какое количество единиц каждого вида оборудования было приобретено.

№174. Швейная фабрика в течение трёх дней производила костюмы, плащи и куртки. Известны объёмы выпуска продукции за три дня и денежные затраты на производство за эти дни:

день	Объём выпуска продукции (единиц)			Затраты (тыс.усл.ед)
	костюмы	плащи	куртки
Первый Второй третий	50 35 40	10 25 20	30 20 30	176 168 184

Найти себестоимость единицы продукции каждого вида.

Примерный вариант контрольной работы

Вариант 1

Выполнить задания:

№1. Вычислить определитель .

№2. Найти матрицу, обратную к матрице .

№3. Решить матричное уравнение

.

№4. Решить систему по формулам Крамера или методом Гаусса

№5. Найти значение матричного многочлена f(A):

f(x)= –x³+2x² – x+3, .

Вариант 2

Выполнить задания:

№1. Вычислить определитель .

№2. Найти матрицу, обратную к матрице .

№3. Решить матричное уравнение .

№4. Решить систему по формулам Крамера или методом Гаусса

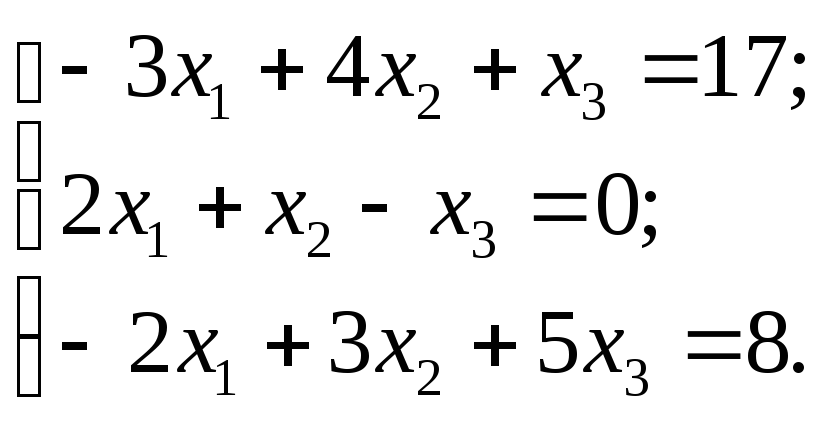
№5. Найти значение матричного многочлена f(A):

f(x)=x³ – 3x²+2x – 2, .

Контрольные вопросы

1. Если матрицы А и В можно умножать, следует ли из этого, что их можно складывать?

2. Если матрицы А и В можно складывать, следует ли из этого, что их можно умножать?

3. Можно ли умножить квадратную матрицу на неквадратную?

4. Может ли произведение неквадратных матриц быть квадратной матрицей?

5. Может ли при умножении ненулевых матриц получиться нулевая матрица?

6. Могут ли совпадать матрицы А и А^Т?

7. Как выглядит матрица ?

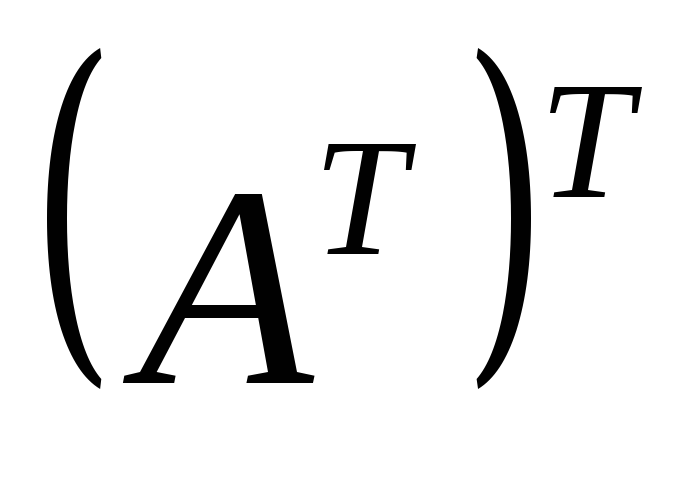8. Верно ли равенство ?

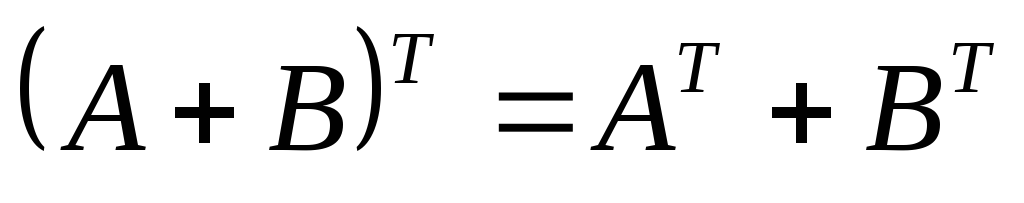9. Верно ли равенство (А+Е)(А – Е)=А² – Е?

10. Верно ли равенство ?

11. Верно ли равенство (А+В)(А – В)=А² – В²?

12. Верно ли равенство ?

13. Могут ли быть эквивалентными матрицы с различным количеством строк? столбцов?

14. Обязательно ли существует произведение ВА, если АВ=Е?

15. Может ли нулевая матрица быть эквивалентной ненулевой матрице?

16. Может ли произведение матриц быть числом?

17. Как изменится произведение матриц А и В, если переставить i-ю и j-ю строки матрицы А?

18. Как изменится произведение матриц А и В, если к i-й строке матрицы А прибавить j-ю строку, умноженную на число с?

19. Как изменится произведение матриц А и В, если переставить i-й и j-й столбцы матрицы В?

20. Как изменится произведение матриц А и В, если к i-му столбцу матрицы В прибавить j-й столбец, умноженный на число с?

21. Всегда ли определитель суммы матриц равен сумме их определителей?

22. Привести пример двух таких матриц, что определитель их суммы равен сумме их определителей.

23. Привести пример двух таких матриц, что определитель их суммы равен сумме их определителей, причём ни один из трёх определителей не равен нулю.

24. Могут ли все алгебраические дополнения некоторой матрицы быть равны соответствующим минорам?

25. Могут ли все алгебраические дополнения некоторой матрицы быть равны соответствующим элементам?

26. Может ли определитель 2-го порядка принимать значение больше, чем определитель 5-го порядка?

27. Может ли определитель изменить знак на противоположный при транспонировании матрицы?

28. Дана квадратная матрица n-го порядка. Чему равна сумма ?

29. Можно ли вычислять миноры, дополнительные к элементам неквадратной матрицы?

30. Как изменится определитель 3-го порядка, если его строки переставить следующим образом: первую — на место второй, вторую — на место третьей, третью — на место первой?

31. Как изменится определитель n-го порядка, если его строки переставить следующим образом: первую — на место второй, вторую — на место третьей, …, (n – 1)-ю — на место n-й, n-ю — на место первой?

32. Может ли ранг матрицы быть равным нулю? меньше нуля? равным 2,5?

33. Ранг матрицы А равен r. Что можно сказать о r(2A)?

R(–A)? r(0 A)?

34. Как может измениться ранг матрицы при транспонировании?

35. Как может измениться ранг матрицы при добавлении к ней одной произвольной строки? Одного произвольного столбца?

36. Как может измениться ранг матрицы при вычёркивании одной строки? Одного столбца?

37. Ранг матрицы А равен r₁, ранг матрицы В равен r₂. Что можно сказать о r(A+B)?

38. Как изменится ранг матрицы при добавлении к ней одной (такой же как первая) строки?

39. Если матрица А не квадратная, может ли существовать такая матрица В, что: а) ВА=Е; б) АВ=Е?

40. Верно ли, что:

а) (2А)^-1=0,5А^-1;

б) (А+В)^-1=А^-1+В^-1;

в) (–Е)^-1= – Е;

г) (АВ)^-1=А^-1В^-1;

д) (А^Т)^-1=(А^-1)^Т;

е) (А²)^-1=(А^-1)²?

41. Верно ли, что:

а) если |A|=0, то |A^-1|=0;

б) если |A|=2, то |A^-1|= –2;

в) если |A|=2, то |A^-1|= –0,5;

г) |A||A^-1|=1?

42. Верно ли, что матрица A^-1 имеет те же размеры, что и матрица А?

43. Следует ли второе утверждение из первого (если матрицы А и В произвольные):

а) АВ=Е, ВА=Е;

б) АВ=2Е, ВА=2Е;

в) А А=Е, А=Е или А= –Е?

44. Следует ли второе утверждение из первого (если матрицы А и В квадратные):

а) АВ=Е, ВА=Е;

б) АВ=2Е, ВА=2Е?

45. Может ли матричное уравнение АХ=В иметь: а) одно решение; б) два решения; в) 17 решений; г) ни одного решения?

46. Равносильны ли уравнения:

а) АХ=В и Х=А^-1В;

б) АХ=В и Х=ВА^-1;

в) АХ=В и Х=АВ^-1;

г) АХ=В и Х=В^-1А?

47. Как изменится матрица А^-1, если в матрице А:

а) поменять местами i–ю и j-ю строки (i–й и j-й столбцы);

б) i–ю строку (столбец) умножить на число ;

в) к i–й строке (столбцу) прибавить j-ю строки (столбец), умноженную на число ?

48. К СЛАУ с n неизвестными дописали произвольное уравнение с n неизвестными. Как при этом изменится количество решений системы?

49. Из несовместной СЛАУ удалили какое-то одно уравнение. Будет ли полученная система совместной?

50. Множества решений двух СЛАУ совпадают. Равны ли расширенные матрицы этих систем? Равны ли ранги этих матриц?

51. Что можно сказать о множестве решений СЛАУ, если ранг r(A) матрицы этой системы и ранг r(A|) расширенной матрицы равны нулю?

52. Что можно сказать о множестве решений СЛАУ с матрицей А и расширенной (A|), если r(A)>r(A|)?

53. Совместная система n линейных уравнений с n неизвестными записана в матричной форме: АХ=В. Будут ли решениями системы оба набора из n чисел:

А^-1В и В^ТА^-1?

54. В системе n линейных уравнений с n неизвестными поменяли местами два уравнения. Изменится ли форма записи решения с помощью обратной матрицы и по формулам Крамера? Изменится ли общее решение?

55. Следует ли, что СЛАУ является однородной, из того, что сумма любых двух решений системы также является её решением?

56. Могут ли совпадать множества решений у двух различных СЛАУ — однородной и неоднородной?