Аудиторные задания

№132. Зная основную матрицу А и расширенную матрицу , записать соответствующую им систему линейных уравнений решить вопрос о её совместности пользуясь теоремой Кронекера-Капелли

.

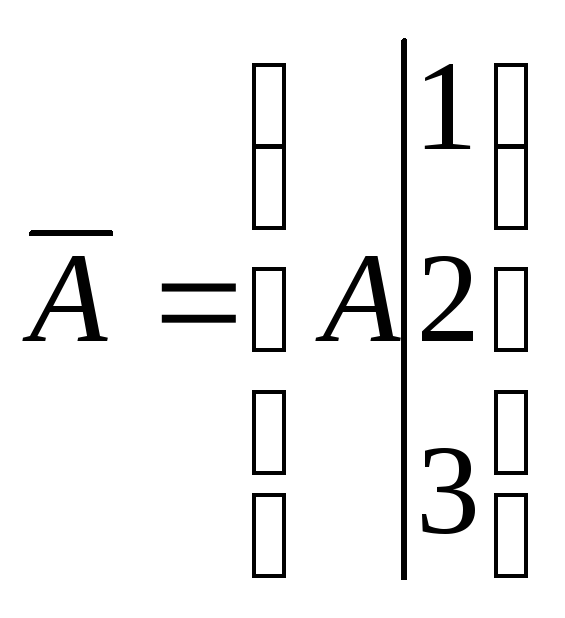Ответ: система несовместна.

№133. Решить систему матричным способом

Ответ: х₁= – 1; х₂=3; х₃=2.

№134. Решить систему с помощью формул Крамера

Ответ: x = –9; y= –10; z =13.

Решить систему методом Гаусса

№135. Ответ: х₁=1; х₂= –2; х₃=1.

№136.

Ответ: х₁= –1+k+t; х₂=3 –k – t; х₃=k; x₄=t.

Решить однородную систему уравнений:

№137. Ответ: х₁=х₂=х₃=0.

№138.

Ответ: х₁=s+2p; х₂=3s+3p; х₃=s; x₄=p.

Домашние задания

№139. Зная основную матрицу А и расширенную матрицу , записать соответствующую им систему линейных уравнений решить вопрос о её совместности пользуясь теоремой Кронекера-Капелли

. Ответ: система не совместна.

Проверить совместность системы уравнений:

№140. Ответ: система несовместна.

№141. Ответ: единственное решение.

№142. Ответ: множество решений.

№143. Решить систему уравнений матричным способом

Ответ: x=1; y=3; z=5.

№144. Решить систему с помощью формул Крамера

Ответ: x=2; y= –1; z=1.

Решить систему методом Гаусса

№145.

Ответ: x₁=1; x₂=2; x₃=3; x₄=4.

№146.

Ответ: x₁= –10t+10; x₂=t; x₃= –16t+15; x₄=4 – 5t.

№147. Решить однородную систему уравнений

Ответ: x₁=14t; x₂=21t; x₃=x₄=t.

Дополнительные задания

Проверить совместимость системы уравнений:

№148.

Ответ: система решений не имеет.

№149. Ответ: система решений не имеет.

№150. Ответ: множество решений.

Решить систему одним из способов (матричным методом, по формулам Крамера, методом Гаусса):

№151.

Ответ: x₁= –1; x₂= –1; x₃=2; x₄=0.

№152.

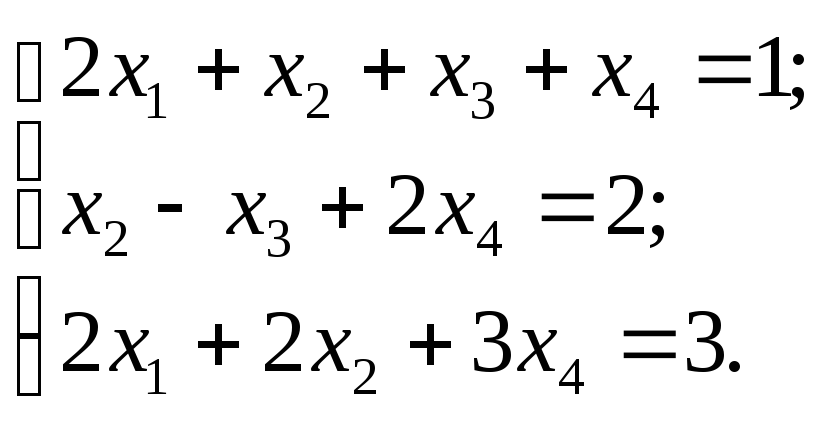
Ответ: , ; х₃=u; x₄=v.

№153. Ответ: x₁=8; x₂=6; x₃=4; x₄=2.

№154. Ответ: x=1; y=3; z=5.

№155. Ответ: x= –1; y=3; z=1.

№156. Ответ: х₁=3; х₂=1; х₃= –1.

№157. Ответ: х₁=1; х₂=2; х₃=3.

№158.

Ответ: система решений не имеет.

№159.

Ответ: x₁= –1; x₂=5; x₃=2; x₄=1.

№160.

Ответ: ; ; х₃=n; x₄=m.

Решение типового варианта индивидуального домашнего задания «Системы линейных алгебраических уравнений»

Задание 1. Дана система линейных алгебраических уравнений

Проверить, совместна ли эта система, и в случае совместности решить её: а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.

► Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований найдём ранги основной матрицы А и расширенной матрицы .

.

Следовательно, RangA=Rang=3=r; число неизвестных n=3; r = n, следовательно, исходная система совместна и имеет единственное решение.

а) Решим её по формулам Крамера: ; ; , где ; ; ; ; х₁= –4, х₂=1, х₃= –2.

б) Для нахождения решения системы с помощью обратной матрицы запишем систему уравнений в матричной форме: ; ; .

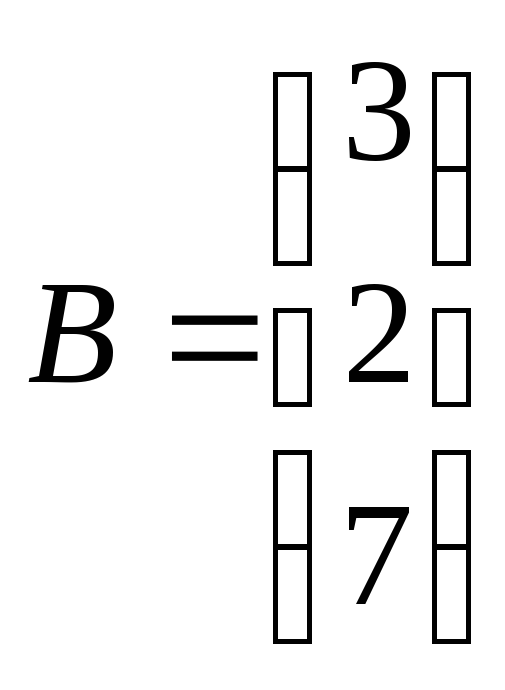Найдём обратную матрицу А^-1 (она существует, т.к. =detA= –160):

А₁₁== –15; А₂₁= –=16; А₃₁== –11;

А₁₂= –= –3; А₂₂==0; А₃₂= –=1;

А₁₃== –14; А₂₃= –=16; А₃₃== –6.

А^-1=.

Решение системы в матричной форме имеет вид: Х=А^-1В.

Х===.

Из полученной матрицы имеем решение системы: х₁= –4, х₂=1, х₃= –2.

в) Решим систему методом Гаусса. Исключим х₁ из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго, затем первое уравнение умножим на 3 и вычтем из третьего:

Из полученной системы находим: х₁= –4, х₂=1, х₃= –2.

Задание 2. Дана система линейных алгебраических уравнений

Проверить, совместна ли эта система, и в случае совместности решить её: а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.

► Проверяем совместимость системы с помощью теоремы Кронекера-Капелли. Для этого найдём ранги основной и расширенной матриц:

.

Rang A=2, Rang=3, т.е. Rang ARang, таким образом, исходная система несовместна. 

Задание 3. Решить однородную систему линейных алгебраических уравнений

► Для однородной системы Rang A=Rang, поэтому она всегда совместна.

⋙Для того чтобы однородная система имела ненулевое решение, необходимо и достаточно, чтобы определитель основной матрицы был равен нулю.

Найдём определитель системы: , следовательно, исходная система имеет нулевое решение: х₁=х₂=х₃=0. 

Задание 4. Решить однородную систему линейных алгебраических уравнений

► Найдём определитель системы: , следовательно, система имеет бесконечно много решений.

Решим данную систему по формулам Крамера в общем виде. Возьмём любые два уравнения системы (например, первое и второе) и найдём её решение. Имеем:

Т.к. определитель из коэффициентов при неизвестных х₁ и х₂ (хотя можно брать и другие пары неизвестных) и переместим члены с х₃ в правые части уравнений:

Решаем последнюю систему по формулам Крамера:

, =17х₃, = –16х₃.

Отсюда находим, что х₁= –, х₂=. Полагая x₃=13k, k–произвольный коэффициент пропорциональности, получаем решение исходной системы:x₁= –17k, x₂=16k, x₃=13k. 