Свойства определителей
Свойство 1. Значение определителя не изменится от замены его строк столбцами, и наоборот (транспонирование).
Пример.
.
Свойство 2. Если поменять местами две любые строки (столбца), то определитель меняет знак.
1)
;
2)
.
Следствие. Определитель, у которого две любые строки (столбца) одинаковы, равен нулю.
Пример.
.
Свойство 3. Если все элементы
какой-нибудь строки (столбца) определителя
умножить на одно и тоже ненулевое число
«
»,
то значение определителя от этого
увеличится (уменьшится) в «
»
раз.
Пример.
.
Умножим все элементы второго столбца
на 4. Получим:
.
Следствие 1. Если все элементы какой-нибудь строки (столбца) определителя обладают ненулевым общим множителем, то его можно вынести за знак определителя.
Пример.
(из последнего столбца вынесли общий множитель 2).
Следствие 2. Определитель, у которого элементы любых двух строк (столбцов) соответственно пропорциональны, равен нулю.
Пример.
.
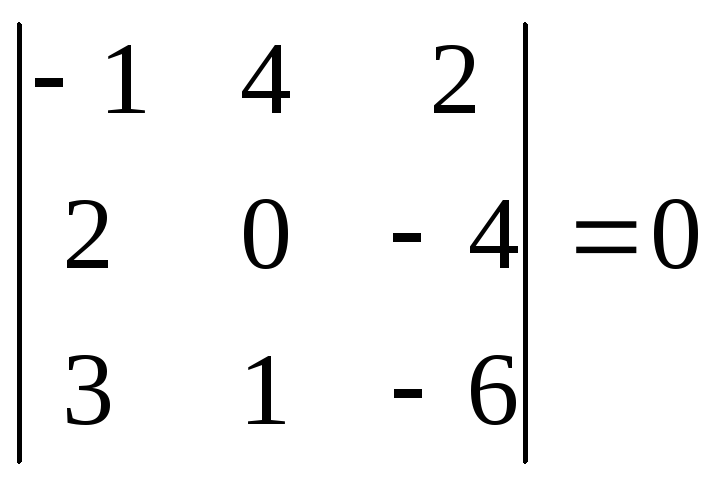Элементы первого и третьего столбцов
соответственно пропорциональны, т.е.
.
Свойство 4. Пусть каждый элемент какой-нибудь строки (столбца) определителя есть сумма двух слагаемых. Тогда определитель равен сумме двух определителей. Причём в одном из них соответствующая строка (столбец) состоит из первых слагаемых, а в другом — из вторых слагаемых.
Пример. Пусть, в определителе первый столбец есть сумма двух слагаемых, тогда
.
Следствие. Определитель не меняет своего значения от прибавления (вычитания) ко всем элементам какой-нибудь строки (столбца) соответствующих элементов любой другой строки (столбца), умноженных на одно и то же ненулевое число.
№8. Пользуясь свойствами, вычислить
определитель
.
► 1) Замечаем, что второй столбец обладает общим множителем 2. Вынесем его за знак определителя. Получим:
.
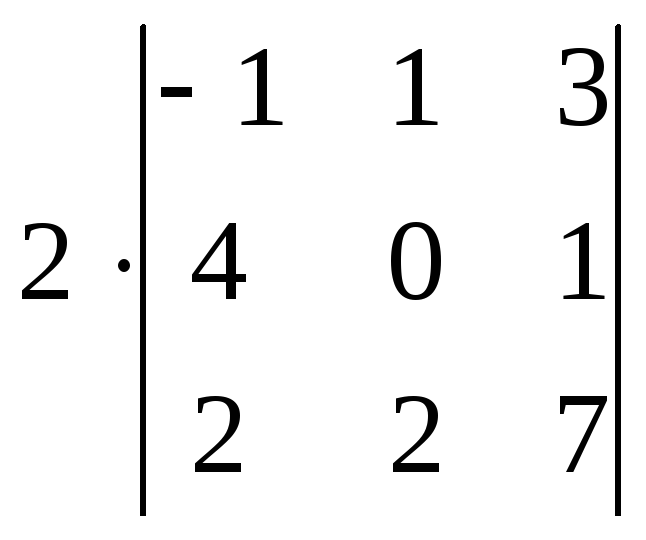2) Если прибавить второй столбец к первому, то полученный первый столбец также будет обладать общим множителем, т.е.:
.
3) Если из третьей строки вычесть вторую, то полученная третья строка также будет обладать общим множителем, т.е.:
.
4) Замечаем, что в определителе одинаковы первая и третья строки. Следовательно, он равен нулю. ◄
№9. Найти М13, М32
для определителя
.
►
Используя
определение минора элемента определителя:
минором Мij
элемента аi
j
называется определитель, полученный
из данного определителя путём вычёркивания
в нём строки и столбца, на пересечении
которых находится элемент aij
имеем:
;
.
◄
№10. Найти А23 и А31
для определителя
.
► Используя определение алгебраического
элемента определителя: алгебраическим
дополнением Аij
элемента aij
данного определителя, называется
минор этого элемента Mij,
умноженный на число
,
т.е.
имеем:
;
.
№11. Вычислить определитель
,
разложением его по элементам второй
строки.
=
◄
№12. Вычислить определитель
,
приведя его к треугольному виду.
► Вычитая первую строку из всех остальных,
получаем
.
◄
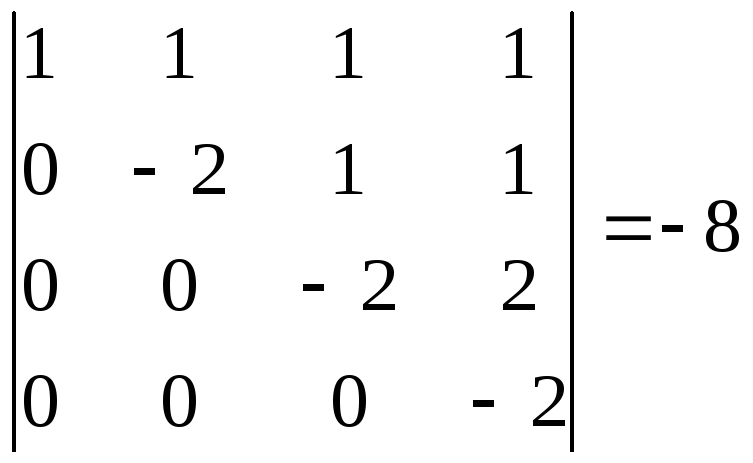Аудиторные задания
Вычислить определитель:
№33.
.
Ответ: 3.
№34.
.
Ответ: 1.
№35.
.
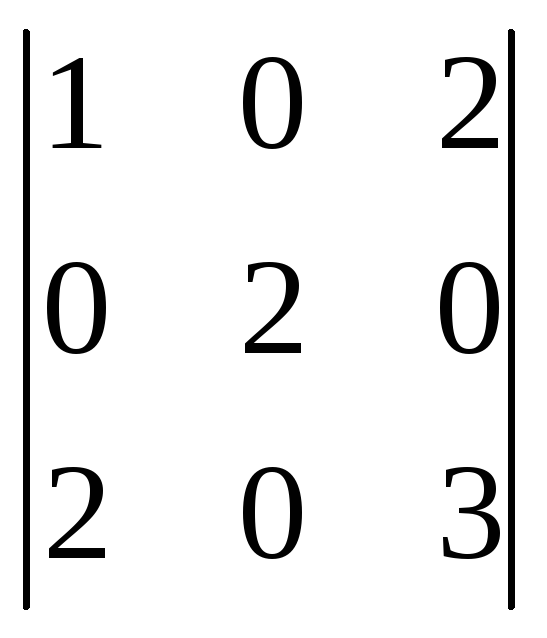Ответ: 2.
№36.
.
Ответ:
–21.
№37. Дан определитель
.
Найти М12; М31; А22;
А32.
Вычислить определитель, используя его свойства:
№38.
.
Ответ: 0.
№39.
.
Ответ: –96.
№40.
.
Ответ: 223.
Решить уравнения:
№41.
.
Ответ: х1= –4;
х2= –1.
№42.
.
Ответ:
.
Решить неравенства:
№43.
.
Ответ: x>3.
№44.
.
Ответ:
.
Вычислить определитель:
№45.
.
Ответ: 17.
№46.
.
Ответ: –4.