2. Закон Рауля.

Обширные экспериментальные исследования Франсуа Мари Рауля (1886 г.) обнаружили, что в типичных случаях давление насыщенного пара растворителя над раствором (Р) равно его давлению над чистым растворителем (Р⁰), умноженному на мольную долю растворителя (N₀) в растворе:

Р = Р⁰ N₀. (7.1)

Из (7.1) следует, что Р < Р⁰, так как N₀ < 1. Уменьшение давления насыщенного пара над раствором может быть объяснено уменьшением поверхности испарения при добавлении растворяемого вещества.

Закон Рауля часто применяется в другой, более удобной для практического использования форме. Для этого правая и левая часть (7.1) делится на Р⁰ и из обоих частей вычитается единица:

, (7.2)

где N - молярная доля растворенного вещества.

Из выражения (7.2) следует, что относительное понижение давления насыщенного пара растворителя над раствором, равно молярной доле растворенного вещества.

На практике большинство растворов обнаруживают более или менее значительные отклонения от закона Рауля, растущие с увеличением концентрации.

Растворы, в которых поведение растворенного вещества и растворителя подчиняются закону Рауля называются абсолютно идеальными или совершенными. Для этих растворов закон Рауля справедлив для любых концентраций растворителя и растворенного вещества. Такие растворы образуют вещества с близкими физическими свойствами и, как следствие, при отсутствии взаимодействия частиц растворителя и растворенного вещества.

Например, если компоненты совершенного раствора А, В, то справедливо соотношение:

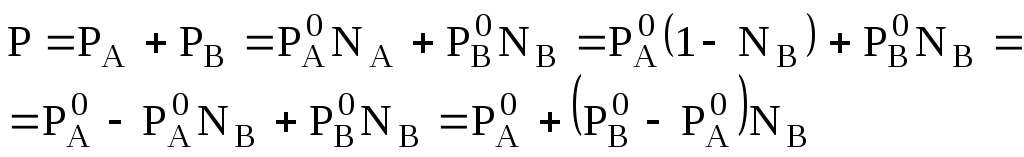, (7.3)

где Р_А, Р_В - давления насыщенных паров компонентов над раствором;

, - давления насыщенных паров компонентов над чистыми компонентами;

N_A, N_B - мольные доли компонентов.

Из (7.3) следует, что давление паров над раствором (Р) линейно изменяется с изменением состава раствора.

3. Температура замерзания и кипения разбавленных растворов (следствия из закона Рауля).

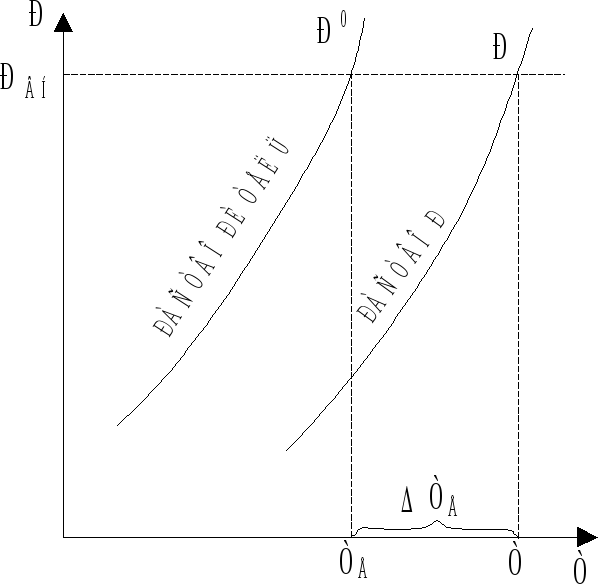
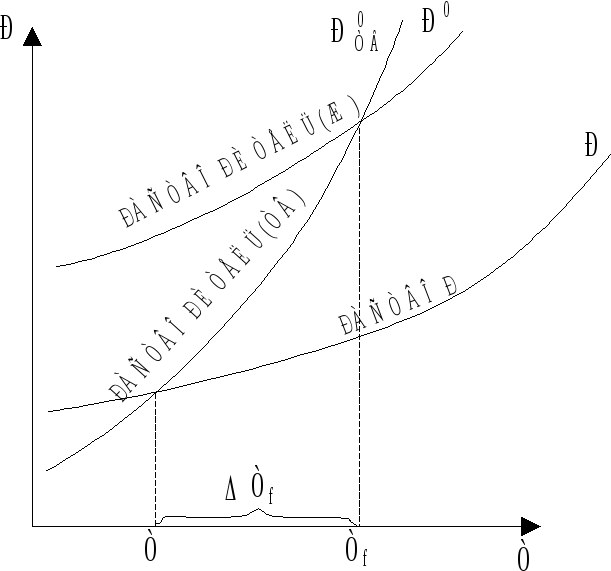
Растворы замерзают при более низкой, а закипают при более высокой температуре, чем чистый растворитель. Эти закономерности относятся только к растворам нелетучих веществ в разбавленных растворах, для которых мольная доля растворенного вещества (N) близка к нулю.

Действительно, если давление пара над раствором понижено (Р < P⁰), то последний нужно нагреть до более высокой температуры, чтобы достигнуть равенства давления пара над раствором и внешнего давления, обеспечивающего кипение (рис. 7.1). Из рис. 7.1 следует, что внешнее давление (Р_ВН) достигается растворителем при температуре Т_Е, а раствором - при Т > T_E, так как Р < P⁰.

Метод исследования, основанный на измерении повышения температуры кипения растворов, называется эбулиоскопическим [ebulliare (лат.) - выкипать], а сам эффект - эбулиоскопическим эффектом.

Условие кипения раствора:

Р = Р⁰ N₀ = Р_ВН, (7.4)

где Р_ВН = 1 (условная единица).

После логарифмирования (7.4) с учетом Р_ВН = 1:

lnР⁰ + lnN₀ = 0,

а после дифференцирования:

.

Из уравнения Клазиуса - Клапейрона следует:

,

поэтому

, (7.5)

где - молярная теплота испарения растворителя.

После разделения переменных и интегрирования (7.5):

Рис. 7.1. Повышение температуры кипения раствора:

Т_Е, Т - температура кипения чистого растворителя и раствора соответственно;

Р_ВН - внешнее давление.

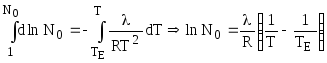
или

,

где .

Для разбавленных растворов , а N << N₀.

Тогда: , причем точность расчета при этом не хуже 1%, если N < 0,02.

Таким образом:

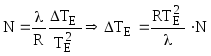. (7.6)

Из (7.6) очевидно, что повышение температуры кипения раствора не зависит от природы растворенного вещества, а определяется лишь его молярной долей в растворе.

Выражению (7.6) можно придать иную форму записи, если концентрацию раствора выразить в единицах его моляльности (m):

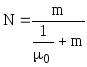, (7.7)

где - молярная масса растворителя.

В разбавленном растворе , поэтому N = m и соотношение (7.6) запишется в виде:

, (7.8)

где = k_Э - эбулиоскопическая постоянная растворителя.

Тогда:

. (7.9)

Эбулиоскопическая постоянная, называемая также молярным повышением температуры кипения, представляет собой величину повышения температуры кипения раствора, содержащего 1 моль растворенного вещества в 1 кг растворителя, по сравнению с температурой кипения чистого растворителя. Каждый растворитель имеет свою эбулиоскопическую постоянную, не зависящую от природы растворенного вещества: k_Э для воды составляет 0,52 К/моль, для бензола 2,57 К/моль.

Эбулиоскопическим методом определяют молярные массы растворенных веществ, однако его используют лишь в тех случаях, когда растворенное вещество нелетучее и растворитель не диссоциирует при температуре кипения раствора.

Другим следствием понижения давления насыщенного пара растворителя над раствором нелетучего растворенного вещества является то, что температура замерзания (кристаллизации) раствора ниже, чем чистого растворителя (рис. 7.2).

Совершенно очевидно, что если при замерзании раствора вымораживается чистый растворитель, то условие замерзания раствора имеет вид:

, (7.10)

где Р - давление пара растворителя над раство-

ром;

- давление пара растворителя над чис-

тым твердым растворителем.

Условие замерзания чистого растворителя:

. (7.11)

Согласно уравнению Клаузиуса - Клапейрона (4.80):

Рис. 7.2. Понижение температуры замерзания раствора:

Т_f, T - температуры замерзания растворителя и раствора соответственно.

и

Совместное решение этих уравнений дает:

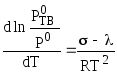, (7.12)

где - молярная теплота плавления.

При температуре замерзания раствора , поэтому 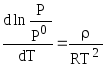, где .

Тогда окончательно:

. (7.13)

Уравнение (7.13) называется уравнением Шредера. Его решение позволяет рассчитать понижение температуры замерзания раствора:

или , (7.14)

где - криоскопическая постоянная растворителя, зависящая как и k_Э только от свойств рас-

творителя.

Из (7.14) следует, что понижение температуры замерзания разбавленных растворов определяется только концентрацией растворенного вещества.

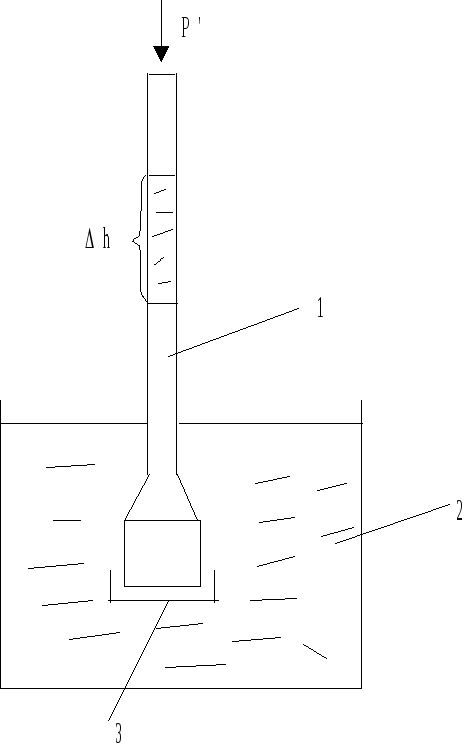Криоскопический метод используется как и эбулиоскопический для определения молярных масс растворенных веществ, однако им пользоваться удобнее, так как для водных растворов в несколько раз больше k_Э, поэтому точность оценок повышается. Так для воды составляет 1,86 К/моль, для бензола - 5,2 К/моль. Как в том, так и в другом методе точность опыта зависит от точности определения . Для повышения точности определения в случае водных растворов пользуются термометром Бекмана, особенностью которого является большая длина шкалы (0,05 м на 1 К). В верхней части термометра имеется резервуар со ртутью, позволяющей изменять количество ртути в рабочей части термометра.