1.3. Множення матриць. Обернена матриця

Означення. Добутком матриці А на матрицю В називається матриця , у якій елемент дорівнює сумі добутків елементів і-го рядка матриці А на відповідні елементи k-го стовпця матриці В.

Якщо де і де , то добуток де

(1.7)

Для існування добутку необхідно, щоб розміри множників були узгоджені: число стовпців першого множника А повинно дорівнювати числу рядків другого множника В.

Приклади. 1. Знайти добуток матриці на матрицю .

.

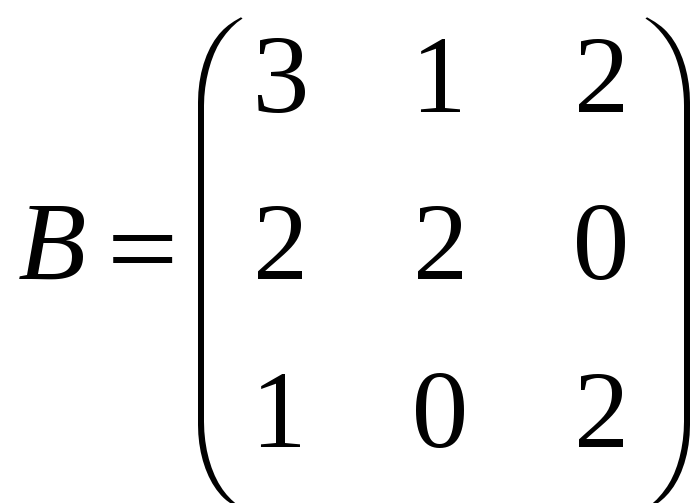Зазначимо, що тут добуток не існує через неузгодженість розмірів.

2. Знайти добутки і , якщо , .

.

.

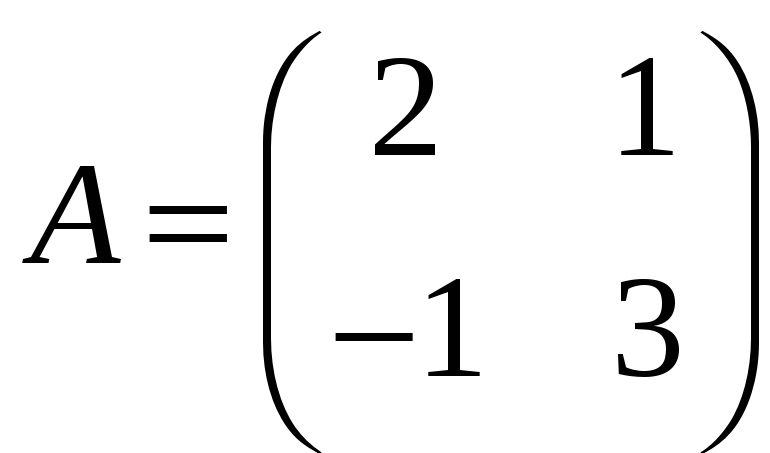Бачимо, що в даному випадку .

Властивості множення матриць.

1. В загальному випадку , як це видно із наведених прикладів. Якщо ж , то матриці А і В називають переставними (комутативними).

2. (λА)·В=А·(λВ)=λ(А·В) – асоціативність відносно множення на число.

3. і – дистрибутивність відносно додавання.

4. асоціативність множення матриць.

5. – одинична матриця відіграє роль одиниці при множенні на будь-яку матрицю А.

6. для будь-якої матриці А.

7. .

8. Для квадратних матриць .

Означення. Матриця називається оберненою до матриці А, якщо , де Е – одинична матриця.

Означення. Квадратна матриця А називається невиродженою, якщо , і виродженою, якщо .

Теорема. Для того, щоб дана матриця А мала обернену, необхідно і достатньо, щоб вона була невиродженою.

Необхідність. Нехай для матриці А існує обернена . Тоді , а значить за властивістю 8:

,

отже і , при чому , і матриця А є невиродженою.

Достатність. Доводиться безпосередньо побудовою оберненої матриці. Процес побудови проілюструємо на прикладі квадратної матриці А третього порядку, але алгоритм залишається в силі для матриці будь-якого порядку.

Алгоритм побудови оберненої матриці.

Нехай .

Для побудови оберненої матриці потрібно:

1. Знайти визначник . Якщо він не дорівнює нулю, то матриця А невироджена і має обернену.

2. В матриці А замінити кожний елемент його алгебраїчним доповненням . Одержимо матрицю

.

3. Транспонувати матрицю :

.

4. Кожний елемент отриманої матриці розділити на визначник даної матриці А, внаслідок чого й одержимо обернену матрицю :

. (1.8)

Доведемо, що це справді так. Множимо за формулою (1.7):

тому що

(формула (1.6)). Аналогічно перевіряється рівність .

Приклад. Знайти матрицю, обернену до матриці

.

1. Знаходимо .

2. Обчислюємо алгебраїчні доповнення:

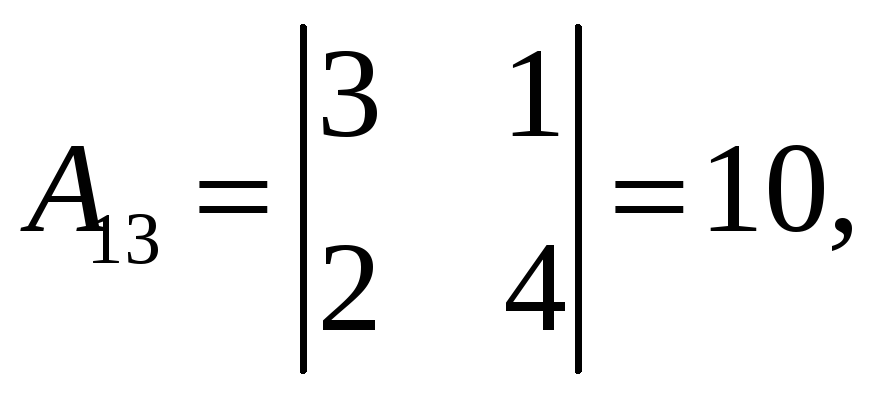
3. Транспонуємо матрицю з алгебраїчних доповнень:

.

4. Знаходимо обернену матрицю:

.

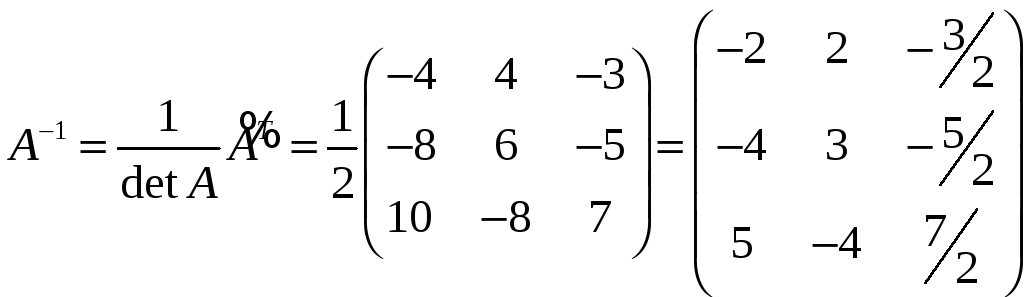Зробимо перевірку:

.

1.4. Система п лінійних алгебраїчних рівнянь з п невідомими. Матричний спосіб розв’язання систем

Нехай задано систему лінійних алгебраїчних рівнянь (СЛАР) з невідомими:

(1.9)

Означення. Система (1.9) називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має розв’язків.

Сумісність системи означає, що існує принаймні один набір чисел , який при підстановці в рівняння системи перетворює їх у вірні рівності.

Запишемо коефіцієнти при невідомих з кожного рівняння системи у відповідний рядок матриці:

. (1.10)

Цю матрицю називають основною матрицею системи (1.9). Розглянемо матричний запис і матричний спосіб розв’язання системи лінійних алгебраїчних рівнянь.

Нехай задано систему лінійних рівнянь з невідомими. Така система називається квадратною. В цьому випадку матриця системи є квадратною. Потрібні міркування проведемо на прикладі системи трьох рівнянь з трьома невідомими, але всі висновки залишаються вірними для будь-якого . Отже розглянемо систему

(1.11)

Запровадимо позначення:

; ; . (1.12)

Тоді, використовуючи правило множення матриць (1.7), систему (1.11) можна записати в еквівалентній матричній формі:

(1.13)

де А –матриця системи, В – задана матриця -стовпець, Х – невідома матриця -стовпець. Розв’язком рівняння (1.13) є такий вектор-стовпець Х, який обертає рівняння (1.13) у вірну рівність.

Якщо , то існує обернена до А матриця . Помножимо рівняння (1.13) почленно зліва на і скористаємося властивостями множення матриць:

.

Отже розв’язок рівняння (1.13) дається формулою

. (1.14)

Ця формула особливо зручна, коли потрібно розв’язувати системи з однією і тією ж матрицею А і різними стовпцями правих частин B.

Таким чином, якщо матриця квадратної СЛАР невироджена, система має єдиний розв’язок.

Приклад. Розв’язати систему

Тут

Матрицю, обернену до матриці А, було обчислено в попередньому пункті:

.

Тоді за формулою (1.14)

.

Відповідь: х=2,5; у=1,5;