1.2. Види матриць. Лінійні дії над матрицями

Означення. Матриця називається нульовою (нуль-матрицею), якщо всі її елементи нулі. Вона позначається О. Наприклад, нульова матриця розміром :

.

Означення. Матриця, одержана з даної матриці А заміною рядків стовпцями і навпаки (перший рядок замінюється на перший стовпець, другий – на другий і т.д.), називається транспонованою матрицею по відношенню до А і позначається . Наприклад,

нехай , тоді .

Елементи матриць А і пов’язані співвідношенням де – число рядків, а – число стовпців матриці А). Очевидно , тобто матриця А є транспонованою по відношенню до . Для квадратної матриці А має місце рівність (див. властивість 1 з п. 1.1).

Означення. Квадратна матриця називається діагональною, якщо всі її елементи, за винятком елементів головної діагоналі, дорівнюють нулю, наприклад , де .

Означення. Діагональна матриця А називається одиничною, якщо всі елементи її головної діагоналі дорівнюють одиниці. Одинична матриця позначається Е, наприклад .

Зазначимо, що .

Означення. Матриця називається трикутною, якщо всі її елементи, розташовані над або під головною чи побічною діагоналлю, дорівнюють нулю. Наприклад

, , .

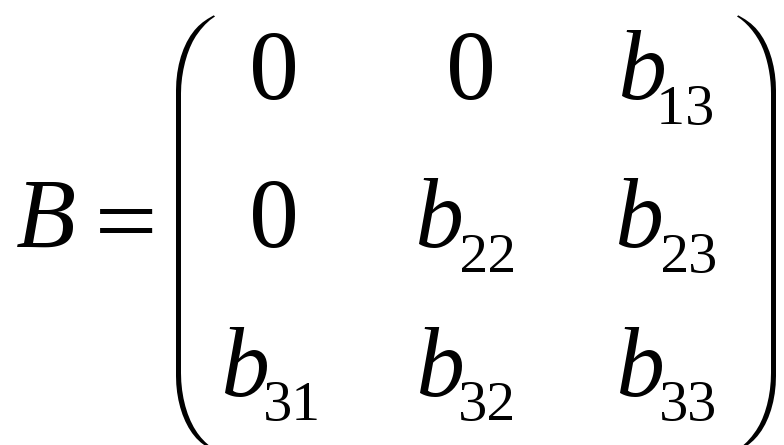Означення. Матриця називається східчастою, якщо кожен її рядок, починаючи з другого, починається з більшої кількості нульових елементів, ніж попередній. Наприклад

Означення. Дві матриці одного розміру рівні, якщо вони поелементно співпадають, тобто А = В, якщо а_ij=b_ij для будь-яких ;.

Означення. Лінійними діями над матрицями називаються додавання (і пов’язане з ним віднімання) і множення матриці на число.

Означення. Сумою двох матриць однакових розмірів називається матриця того ж розміру, елементи якої дорівнюють сумам відповідних елементів матриць-доданків. Наприклад

.

Таким чином додавання матриць виконується аналогічно додаванню числових векторів, отже має такі самі властивості, зокрема:

1. комутативність: ,

2. асоціативність: ,

3. А + О = О + А = А, де О – нуль-матриця.

Матриці А і В називаються взаємно протилежними, якщо О, де О – нуль-матриця. Матриця, протилежна матриці А, позначається і її елементи протилежні за знаком відповідним елементам матриці А.

Різницею матриць є сума матриці А і матриці, протилежної матриці В, тобто

.

Означення. Добутком матриці А на число λ називається матриця λА, елементи якої є добутками елементів матриці А на це число. Наприклад

.

Множення матриці на число має такі властивості:

1) λ(μА)=(λμ)А – асоціативність відносно числових множників;

2) (λ + μ)А=λА + μА – дистрибутивність відносно числового множника;

3) λ(А + В)= λА +λВ – дистрибутивність відносно матричного множника;

4) λ·О = О для будь-якого числа λ;

5) = О для будь-якої матриці А;

6) для будь-якої матриці А.

Зазначимо, що результати лінійних дій над матрицями даного розміру дають матриці такого ж розміру.

Приклад. Обчислити матрицю С=3А – 2В, де

, .

Згідно з означенням добутку матриці на число,

3А=, – 2В=.

Далі, 3А – 2В=3А +(– 2В)=.

Таким чином, С=.