Пример 2.12

Рассмотрим задачу Эйлера "О ходе шахматного коня". Требуется шахматным конем обойти вся поля доски и вернуться в исходное поле, при этом ни разу не бывая в одном поле более одного раза.

Если поля шахматной доски принять за вершины графа G_{8  8} , ребрами считать возможность коня согласно шахматным правилам перемещаться с поля  u на поле v  ({u, v}  G_{8  8} , если конь может пойти с поля u на поле v), то это задача о гамильтоновом цикле. Задача Эйлера имеет хорошо известные многочисленные исследования и решения. Попробуем решить эту задачу для шахматной доски 5  7. Ей соответствует граф G_{5  7} . Заметим, что согласно шахматным правилам конь не может пойти с некоторой клетки на другую клетку того же цвета, т.е. рассматриваемый граф является двудольным. Так как граф G_{5  7}  содержит 35 вершин, то он не является гамильтоновым, так как нарушаются необходимые условия существования гамильтонова цикла в двудольном графе. В то же время гамильтонова цепь в таком графе может существовать, так |17 – 18| = 1.

2.5. Планарные графы

             Плоские графы

             Формула Эйлера

             Критерий планарности Понтрягина-Куратовского

Плоские графы

Граф G называется плоским, если он изображен на плоскости без пересечения ребер (кроме соединения ребер в вершинах).     

Говорят, что граф G изоморфно укладывается на плоскость, если он изоморфен плоскому графу.

Граф G называется  планарным, если он изоморфно укладывается на плоскость.

Гранью плоского графа G называется часть плоскости, не содержащая вершин и ребер, ограниченная простым циклом. Конечная грань графа называется внутренней, а бесконечная – внешней.

Замечание. Если у графа, содержащего простой цикл, удалить одно ребро из этого цикла, то количество внутренних граней этого графа уменьшится на единицу.

Пример 2.13

1.      На рис. 2.21,а  изображен плоский граф, у которого грани 1, 2, 3 – внутренние, а грань 4 – внешняя.

2.      На рис. 2.21,б  изображен планарный граф, изоморфный плоскому графу (рис. 2.20,в).

 

Рис. 2.21. Планарные графы

Формула Эйлера

Пусть G – планарный граф с n  вершинами, m   ребрами и g  гранями.

Лемма 2.4. Число g граней плоского связного графа G  равно:  g = 1 + ,

где  – цикломатическое число графа G.

Доказательство. По смыслу числовая характеристика    (см. разд. 2.3) равна количеству ребер, которые нужно удалить из простых циклов графа, чтобы получить его  остовное  дерево. Удаление каждого такого ребра в плоском графе приводит к уменьшению количества внутренних граней графа G на единицу. Из определений планарного графа и внутренних граней следует, что дерево представляет собой плоский граф с одной внешней гранью (так как он связен и не имеет циклов). Следовательно, число граней графа G определяется формулой: g = 1 + , что и требовалось доказать.

Теорема 2.13. В любом связном плоском графе числа n, m, g удовлетворяют равенству

n – m + g = 2      –      формула Эйлера.

Доказательство. По лемме 2.4 g = 1 + , где цикломатическое число графа G:       = 1 + m – n. Откуда, g = 1 + (1 + m – n)  или окончательно:

n – m + g = 2.

Следствие. Если G связный плоский (n, m) – граф, в котором каждая внутренняя грань имеет t ребер, то справедлива оценка:

.                                                        (_*)

Доказательство. Оценим число граней графа. Ясно, что число ребер внешней грани не меньше, чем t. Так как каждое ребро входит в две грани, то получаем неравенство: gt  2m или g  2m  t. Подставив оценку для числа граней в формулу Эйлера, найдем:  2  n – m + 2m  t.  После ряда преобразований получим неравенство: m(t – 2)  t(n-2) откуда и получается  доказываемая оценка.

Утверждение 2.9. Граф K₅ не планарный.

Доказательство. Пусть граф K₅ (рис. 2.22) – планарный и граф G – плоский граф, изоморфный K₅. Так как K₅ – полный 5-вершинный граф, то граф G имеет  n = 5,  m = 10, причем каждая грань его содержит t = 3 ребра. Тогда, подставляя эти значения в неравенство (_*) , получаем:

, 10  9   –   

противоречие. Следовательно, K₅ – это не планарный граф.

Утверждение 2.10. Граф K_3,3 не планарный.

Доказательство. Пусть граф K_3,3 (рис. 2.23) – планарный и граф G – плоский граф, изоморфный K_3,3. Так как K_3.3 – полный 6-вершинный двудольный граф, то граф G имеет  n = 6, m = 9, причем каждая грань его содержит t = 4 ребра. Тогда, подставляя эти значения в неравенство (_*), получаем:

, 9  8  –  

противоречие. Следовательно, K_3,3 – это не планарный граф.

Рис. 2.23. Не планарный граф K_3,3

 

Замечание. Следует отметить, что неравенство (_*) является необходимым условием планарности графа. Иначе говоря, если это неравенство справедливо, то это еще не означает, что этот граф планарный. Действительно, применим это неравенство к графу изображенному на рис. 2.24.

 

Рис. 2.24. Не планарный граф.

 

Данный граф имеет n = 9 вершин, m = 20 ребер, простые циклы, ограничивающие внутренние грани, с числом ребер t = 3. Следовательно, в результате получаем:

 -

противоречия нет. Однако рассмотренный граф не является планарным. Что непосредственно следует из теоремы Понтрягина-Куратовского.

Планарный граф G называется максимальным планарным графом, если добавление к нему одного ребра нарушает свойство планарности. Приведем условия максимальности планарного графа.

Утверждение 2.11. Если планарный граф максимальный, то все его внутренние грани содержат по три ребра.

Доказательство. Пусть G – максимальный планарный граф, тем не менее,  у него существует внутренняя грань, ограниченная простым циклом, с длиной не равной 3.

Так как минимальная длина простого цикла не может быть меньше трех,  то такая грань содержит 4 или более ребер. Следовательно, в цикле, ограничивающем данную грань, найдутся не смежные вершины. Добавление  ребра, инцидентного этим вершинам, не нарушит планарности графа G так, как  он изоморфно укладывается на плоскость. Это противоречит максимальности графа.

Пусть (n, m) граф максимальный. Согласно утверждению 2.11 число ребер каждой его внутренней грани t = 3, тогда оценка общего количества ребер максимального планарного графа будет,

.

Оценка: m  3n – 6 будет справедливой для любого планарного графа (следует из определения максимального планарного графа (n, m)).

Утверждение 2.12. Каждый планарный (n, m) граф имеет хотя бы одну вершину степени   5.

Доказательство. Пусть все вершины  планарного (n, m) графа G имеют степень   6. Для всех графов справедливо (см. разд. 1.1) соотношение: , из этого равенства в нашем случае для графа G имеем: 6n  2m, откуда получается первое неравенство: m  3n. С другой стороны, для планарного графа справедлива оценка:  m  3n – 6. Вычитая из первого неравенства второе, получаем: 0  6 – противоречие. Следовательно, G – планарный (n, m) граф имеет вершину степени, меньшей или равной 5.

 

Рис. 2.24. Не планарный граф

 

Операции редуцирования

Вершина v в графе  G называется проходной, если ее степень: (v) = 2.

Пусть задан граф G = (V, E).

Добавление проходной вершины. Добавление проходной вершины w производится по следующей схеме:

1)      удаляется ребро e  E, инцидентное вершинам u, w  V;

2)      добавляются ребра e' = {u, w} и e'' = {w, v}.

В результате, получается граф: G' = (V', E'),

где V' = V  {w}, E'= E\{e}  {e', e''}.

Удаление проходной вершины.  Удаление проходной вершины w производится по следующей схеме:

1)      удаляется ребро e', инцидентное вершинам u, w  V, и ребро e'', инцидентное вершинам w, v  V;

1)      добавляется ребро e, инцидентное вершинам u, v  V.

В результате, получается граф: G' = (V', E'),

где V' = V\{w}, E'= E\{e', e''}    {e}.

Стягивание ребра. Стягивание ребра e инцидентного вершинам u, v в графе G = (V, E) производится по следующей схеме:

1)           удаляется ребро e, инцидентное вершинам u, v  V;

2)           склеиваются вершины u, v, образуя вершину uv  V.

В результате, получается граф G' = (V', E'), где V' = V\{u, v}  {uv} , E'= E\ {e} (рис. 2.25).

В общем, операции добавления проходной вершины, удаления проходной вершины и стягивания ребра называются операциями редуцирования.

 

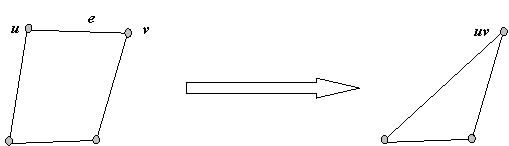
Рис. 2.25. Операция стягивания ребра

Критерий планарности Понтрягина-Куратовского

Два графа гомеоморфные, если один из них может быть получен из другого  применением конечного числа раз операций редуцирования.        

Если графы гомеоморфные, то они планарные или не планарные одновременно.

Теорема 2.14. (Понтрягина-Куратовского). Граф G планарный тогда и только тогда, когда он не содержит подграфов, гомеоморфных  графам K₅ или K_3,3.

(Без доказательства).