4.5. Пример счетчика с прямым/обратным счетом

На рис. 3.47 показана конфигурация счетчика с прямым счетом (суммирующего счетчика), реализованного посредством трех триггеров. Этот счетчик считает в таком порядке: 0,1,2, …7,0,.... Для обратного счета, то есть счета в порядке 0,7,6, .применяются похожие схемы. При построении этих простых схем используется заложенная в Т-триггере возможность переключения состояний.

Сейчас же мы рассмотрим возможность реализации счетчиков на основе D-триггеров. В частности, речь пойдет о структуре счетчика, который способен считать как в прямом, так и в обратном порядке, в зависимости от значения на внешнем управляющем входе. Для того чтобы приводимый пример не оказался слишком большим, мы ограничимся счетом по модулю 4, для которого достаточно двух битов состояния, представляющих четыре возможных значения счетчика.

Счетчик будет сконструирован на основе стандартной технологии синтеза последовательных схем. Такая схема считает в прямом направлении, если входной сигнал х равен 0, и в обратном, если входной сигнал равен 1. Текущее значение счетчика будет изменяться на отрицательном фронте тактового сигнала. Предположим, что нас особо интересует состояние счетчика в тот момент, когда мы досчитаем до 2. Поэтому при значении счетчика 2 мы будем выдавать выходной сигнал z = 1, а все остальное время сигнал z будет равен 0.

Такой счетчик можно реализовать как последовательную схему. Для того чтобы определить новое значение счетчика, которое будет установлено после очередного тактового импульса, достаточно знать значение х и текущее значение счетчика. Предшествующие его значения для этого не нужны. Если текущее значение равно 2 и х = 0, следующим значением будет 3. И не важно, получено текущее значение путем прямого счета от 1 или путем обратного счета от 3.

Прежде чем показать, как реализуется такая схема, давайте опишем ее поведение с помощью диаграммы состояний. У нашего счетчика имеется четыре разных состояния: S0, S1, S2 и S3. Диаграмма состояний — это граф, в котором состояния представлены окружностями (иногда называемыми узлами). Переходы между состояниями представлены стрелками с надписями. Связанная со стрелкой надпись указывает, какое значение переменной х вызывает данный переход и какое значение счетчика получается в результате. Диаграмма состояний для нашего счетчика с прямым/обратным счетом приведена на рис. 4.8. Например, стрелка, исходящая

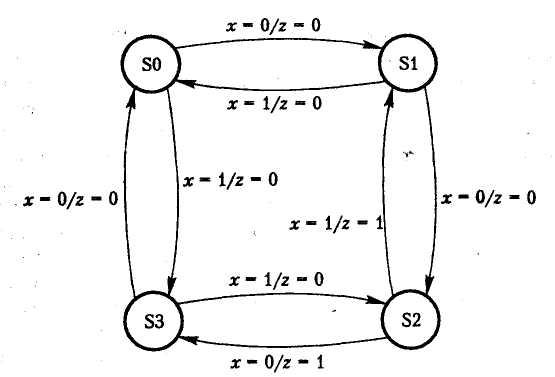
Рис. 4.8. Диаграмма состояния для счетчика с прямым/обратным счетом по модулю 4, сигнализирующего о значении 2

от состояния S1 (счетчик = 1) при х = 0, указывает на состояние S2. При этом сообщается, что пока схема находится в состоянии S1 и х = 0, выходное значение z должно быть равным 0. Стрелка, ведущая от узла S2 к узлу S3, указывает, что когда х = 0, на следующем такте будет выполнен переход в состояние S3, а выходное значение z будет установлено в 1.

Обратите внимание, что диаграмма состояний описывает функциональное поведение счетчика вне какой бы то ни было связи с его конкретной реализацией. Так, рис. 4.8 может соответствовать цифровой схеме, механическому счетному устройству или компьютерной программе. Подобные диаграммы позволяют описывать любую систему с последовательным поведением.

В качестве альтернативы диаграмме состояний для представления той же информации можно воспользоваться таблицей состояний (табл. 4.1).

Таблица 4.1

Состояния для счетчика с прямым/обратным счетом

Текущее состояние

Следующее состояние

Выход zг

Х=0

Х= 1

Х=0

Х=1

В ней описаны переходы из каждого текущего состояния в следующие состояния, определяемые входным значением х. Выходной сигнал z определяется текущим состоянием схемы и входным значением х. Определив функциональное поведение счетчика, можно переходить к его физической реализации.

Для того чтобы закодировать все четыре состояния счетчика, достаточно двух битов. Обозначим их как у₂ (старший бит) и у₁ (младший бит). Состояния счетчика, определяемые значениями переменных у₂ и y₁, мы 6удем записывать в форме у2у1. У нашего счетчика четыре состояния у2у1: S0 = 00, S1 = 01, S2 = 10 и S3 = 11.

Как видите, это просто двоичная запись чисел из диапазона от 0 до 3, применяемая для обеспечения наглядности счета. Переменные у2 и у1 называются переменными состояния последовательной схемы. При указанных значениях этих переменных таблицу состояний для нашего примера можно переписать так, как показано в табл. 4.2. Для обозначения следующих состоянии в ней используются переменные Y2 и Y1.

Таблица А.49

Значения состояний для примера, приведенного на рис. А.48

Текущее состояние	Следующее состояние		Выход z
	Х=0	Х=1	Х=0	Х=1
Y2Y1	Y2Y1	Y2Y1
0 0 0 1 1 0 1 1	0 1 1 0 1 1 0 0	1 1 0 0 0 1 1 0	0 0 1 0	0 0 1 0

Мы могли бы выбрать и другие обозначения состояний у2у1. В частности, они могут быть такими: S0 = 10, S1= 11, S2 = 01 и S3= 00. Но такие обозначения не совсем логичны, хотя схема прекрасно бы функционировала. Реализация различных состояний обычно требует разных затрат.

Мы планировали создать нашу схему на основе D-триггеров, в которых значения двух переменных состояния будут сохраняться между последовательными тактовыми импульсами. Выход Q каждого триггера будет представлять переменную текущего состояния, а вход D — переменную следующего состояния Yi. Заметьте, что Yi является функцией переменных у2, у1 и х (табл. 4.2).

На основе представленной здесь таблицы для функций Y2 и Y1 можно составить вот такие выражения:

Y2 = у1 + у2 + х + у2у1х = у2у1х