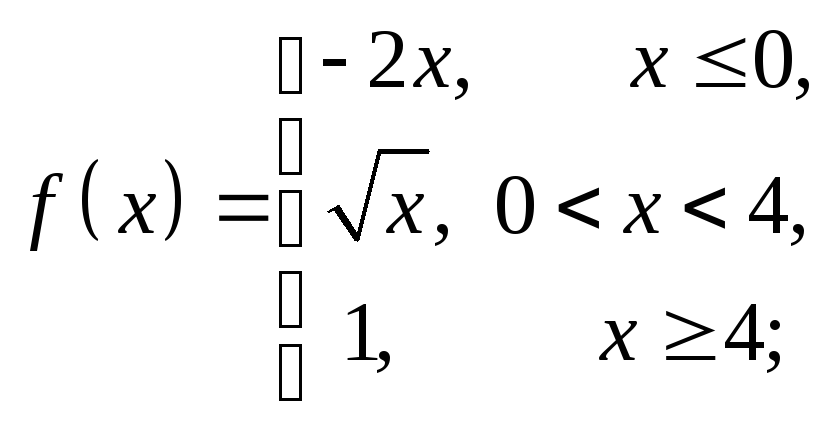5.7. Равномерная непрерывность. Теорема Кантора
Пусть
функция
![]() непрерывна на некотором промежутке
непрерывна на некотором промежутке
![]() .
В определении 2 непрерывности функции
в точке величина
.
В определении 2 непрерывности функции
в точке величина
![]() зависит не только от
зависит не только от
![]() ,
но и от
,
но и от
![]() .
Причем, чем круче график функции в
окрестности точки
.
Причем, чем круче график функции в
окрестности точки
![]() ,
тем меньше
,
тем меньше
![]() (рис. 55). Отказ от зависимости
(рис. 55). Отказ от зависимости
![]() от точки
от точки
![]() приводит к понятию равномерной
непрерывности.
приводит к понятию равномерной
непрерывности.
Определение.
Функция
![]() называется равномерно-непрерывной на
промежутке
называется равномерно-непрерывной на
промежутке
![]() ,
если для любого
,
если для любого
![]() найдется такое
найдется такое
![]() ,
что для любых двух точек
,
что для любых двух точек
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Иными
словами, равномерная непрерывность
означает выполнение неравенства
![]() независимо от положения точек
независимо от положения точек
![]() и
и
![]() на промежутке
на промежутке
![]() ,
лишь бы разность
,
лишь бы разность
![]() была достаточно малой.
была достаточно малой.
Для
равномерно-непрерывной функции величина
![]() зависит только от
зависит только от
![]() и является общей для всего промежутка
и является общей для всего промежутка
![]() .
.
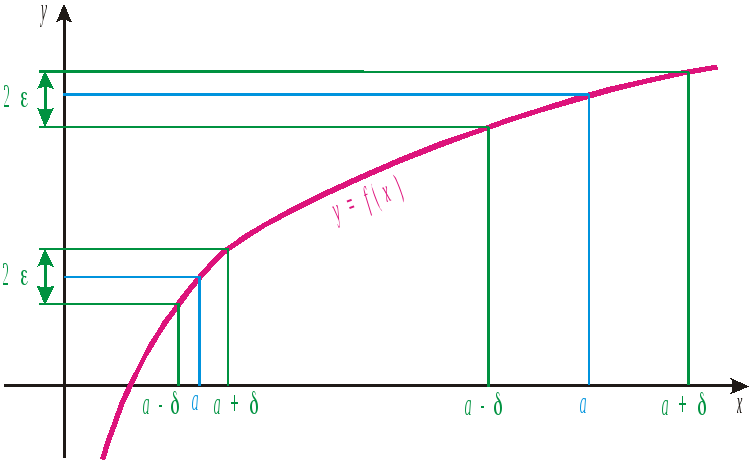
Рис. 55
Теорема Кантора.
Если функция непрерывна на отрезке
![]() ,
то она равномерно непрерывна на этом
отрезке.
,
то она равномерно непрерывна на этом
отрезке.
Доказательство.
Предположим, что функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
но не является равномерно непрерывной
на этом сегменте.
Тогда для некоторого
,
но не является равномерно непрерывной
на этом сегменте.
Тогда для некоторого
![]() и для любого сколь угодно малого
и для любого сколь угодно малого
![]() найдутся две точки
найдутся две точки
![]() и
и
![]() отрезка
отрезка
![]() такие, что
такие, что
![]() но
но
![]() .
Выберем
бесконечно малую последовательность
положительных чисел
.
Выберем
бесконечно малую последовательность
положительных чисел
![]() с натуральными
с натуральными
![]() .
Тогда, можно утверждать, что для указанного
.
Тогда, можно утверждать, что для указанного
![]() и для любого номера
и для любого номера
![]() найдутся две последовательности
найдутся две последовательности
![]() и
и
![]() отрезка
отрезка
![]() такие, что
такие, что
![]() но
но
![]() .
Так как
последовательность
.
Так как
последовательность
![]() состоит
из точек отрезка
состоит
из точек отрезка
![]() ,
то она ограничена и по теореме Больцано
Вейштрасса из нее можно выделить
сходящуюся подпоследовательность
,
то она ограничена и по теореме Больцано
Вейштрасса из нее можно выделить
сходящуюся подпоследовательность
![]() ,
,
![]() .
Предел указанной подпоследовательности
будет также принадлежать данному
отрезку. В силу неравенства
.
Предел указанной подпоследовательности
будет также принадлежать данному
отрезку. В силу неравенства
![]() соответствующая
подпоследовательность
соответствующая
подпоследовательность
![]() будет сходиться к той же самой
будет сходиться к той же самой
![]() .
Поскольку
функция
.
Поскольку
функция
![]() непрерывна
в каждой точке указанного отрезка, она
непрерывна и в точке
непрерывна
в каждой точке указанного отрезка, она
непрерывна и в точке
![]() .
Но тогда, в силу определения непрерывности
по Гейне, обе подпоследовательности
соответствующих значений функции
.
Но тогда, в силу определения непрерывности
по Гейне, обе подпоследовательности
соответствующих значений функции
![]() и
и
![]() обязаны
сходиться к
обязаны
сходиться к
![]() ,
т.е. разность yказанных
подпоследовательностей
,
т.е. разность yказанных
подпоследовательностей
![]() обязана быть бесконечно малой, что
противоречит неравенству
обязана быть бесконечно малой, что
противоречит неравенству
![]() ,
справедливому для всех номеров
,
справедливому для всех номеров
![]() и потому для всех номеров
и потому для всех номеров
![]() .
Полученное противоречие доказывает,
что наше утверждение о том, что непрерывная
на отрезке функция не является равномерно
непрерывной на нем, является неверным.
.
Полученное противоречие доказывает,
что наше утверждение о том, что непрерывная
на отрезке функция не является равномерно
непрерывной на нем, является неверным.
Отметим, что эта теорема неверна для интервала или полуинтервала.
Пример.
Функция
![]() непрерывна на интервале
непрерывна на интервале
![]() ,
однако она не является равномерно-непрерывной
на этом интервале. В самом деле, если
,
однако она не является равномерно-непрерывной
на этом интервале. В самом деле, если
![]() ,
,
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
(*)
.
(*)
Если
![]() ,
то, каково бы ни было
,
то, каково бы ни было
![]() ,
из условия (*) следует, что всегда найдется
такое
,
из условия (*) следует, что всегда найдется
такое
![]() ,
для которого
,
для которого
![]() ,
,
![]() ,
,
![]() ,
а
,
а
![]() .
Это и означает, что функция
.
Это и означает, что функция
![]() не является равномерно непрерывной на
интервале
не является равномерно непрерывной на
интервале
![]() .
.
5. Задачи Группа а
1. Задана функция
![]() и два значения аргумента
и два значения аргумента
![]() и
и
![]() .
Требуется: 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы в точке разрыва слева и справа;
3) сделать схематический чертеж.
.
Требуется: 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы в точке разрыва слева и справа;
3) сделать схематический чертеж.
1)
![]() ,
,
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ,
,
![]() ;
;
6)
![]() ,
,
![]() ,
,
![]() ;
;
7)
![]() ,
,
![]() ,
,
![]() ;
;
8)
![]() ,
,
![]() ,
,
![]() ;
;
9)
![]() ,
,
![]() ,
,
![]() ;
;
10)
![]() ,
,
![]() ,
,
![]() .
.
2. Найти точки разрыва функции, если они существуют. Сделать чертеж.
1)
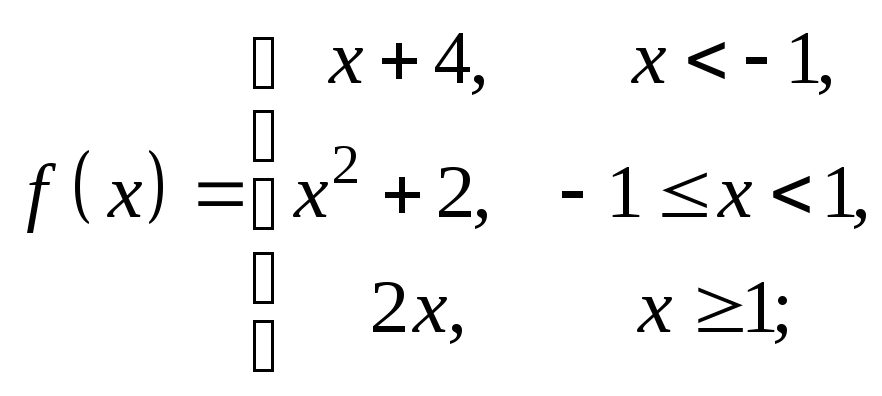 2)
2)
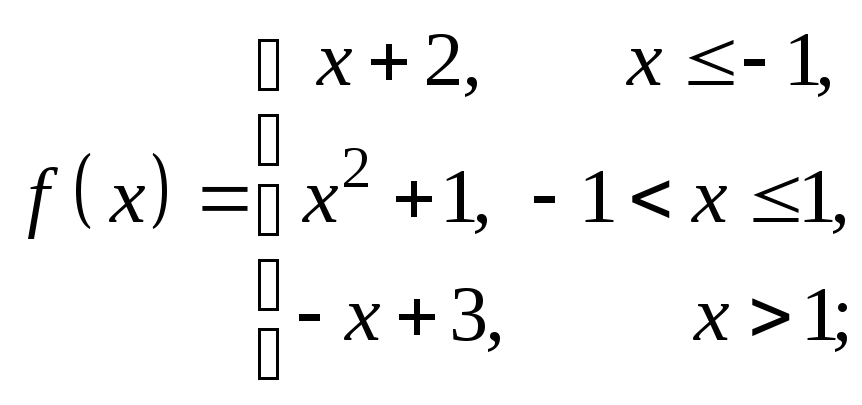
3)
 4)
4)
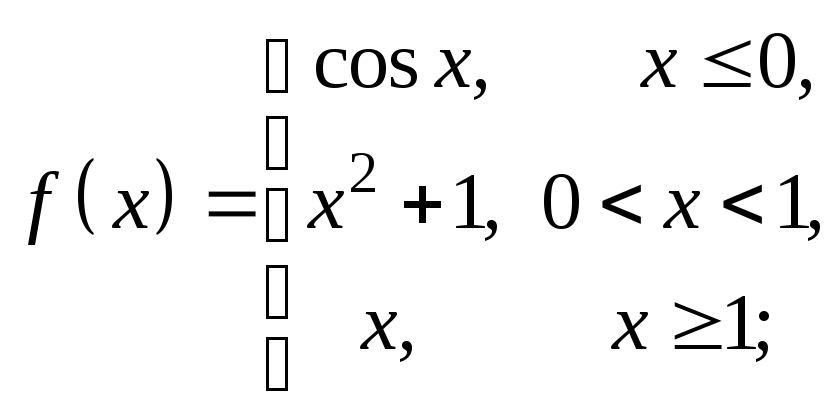
5)
 6)
6)
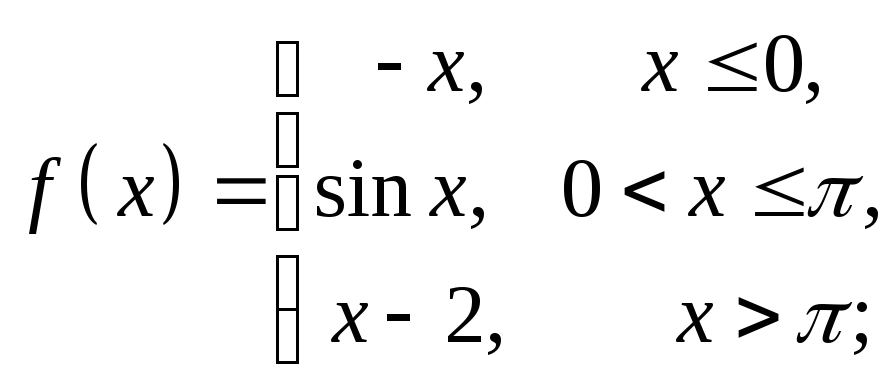
7)
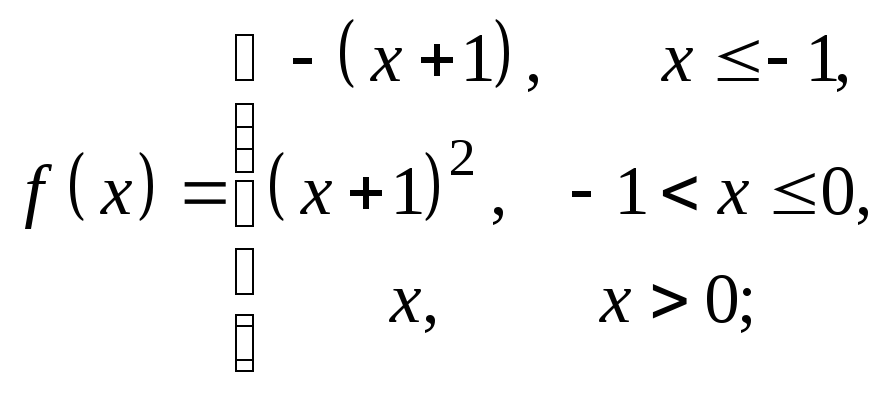 8)
8)
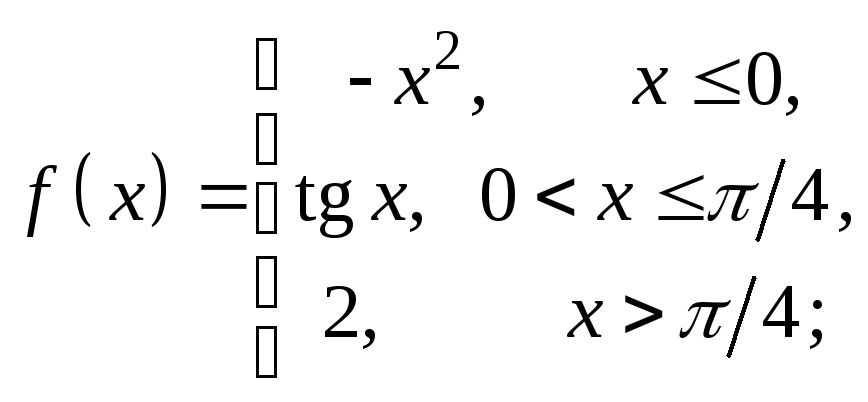
9)
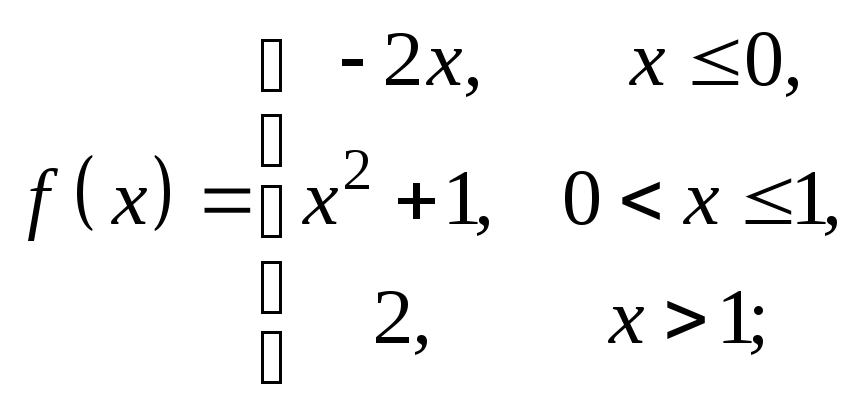 10)
10)