Вопросы для подготовки
-
Какие существуют способы задания плоскости на чертеже?
-
Какое положение может занимать плоскость относительно плоскостей проекций?
-
Что такое следы плоскости? Как находят следы плоскости?
-
Что такое линии уровня в плоскости?
-
Что такое линии наибольшего наклона плоскости к плоскостям проекций? Каков алгоритм их построения?
-
Как найти недостающие проекции точек и прямых, лежащих в плоскости?
-
Как достроить недостающую проекцию плоской фигуры?
-
Какое положение по отношению друг к другу могут занимать плоскости?
-
Что является результатом пересечения двух плоскостей? Сколько точек необходимо найти для построения линии пересечения плоскостей?
-
По какому алгоритму в общем случае решается задача построения линии пересечения двух плоскостей?
-
Каково условие параллельности двух плоскостей?
-
Какое положение по отношению друг к другу могут занимать прямая и плоскость?
-
Как определяется видимость прямой относительно плоскости?
-
Каково условие параллельности прямой и плоскости?
Задачи
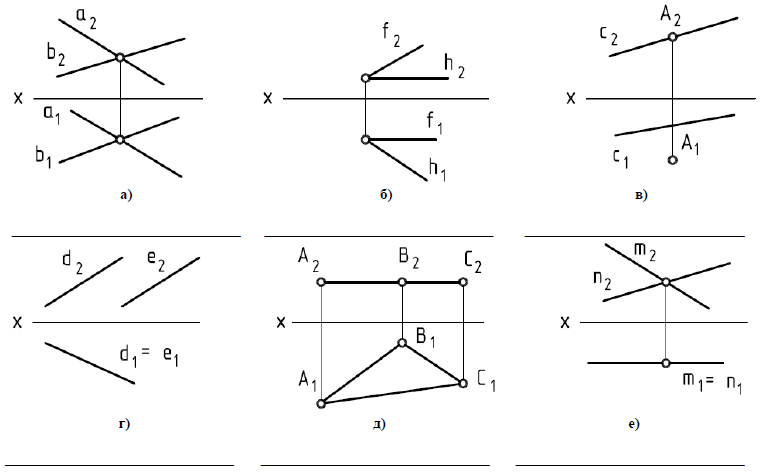
3.1. Определить положение плоскостей заданных различными способами относительно плоскостей проекций, записать их название.
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
|
3.2. Через точку К провести прямую m, параллельную отрезку АВ и прямую n, делящей отрезок АВ пополам. Сколько различных плоскостей задано на чертеже? |
|
3.3. Определить положение плоскости, заданной прямыми а и b, относительно плоскостей проекций. Найти недостающие проекции точек А и В, принадлежащих плоскости. Через точку В провести в плоскости горизонталь и фронталь.
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
|
3.4. По проекциям точек А2 и В1 построить отрезок АВ принадлежащий плоскости (m, n). |
|
3.5. Прямую а заключить в плоскость, задав ее следами:
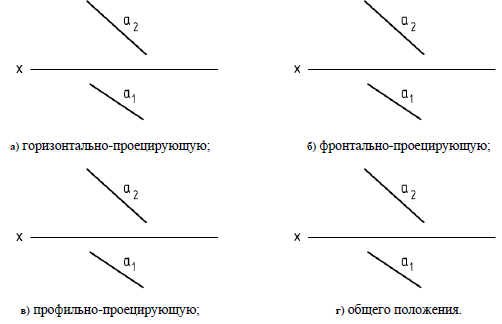
3.6. Достроить недостающую проекцию треугольника ABC, принадлежащего плоскости .
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
|
|
|
3.7. Построить недостающие проекции прямых a и b, если прямые a, b, c и точка A лежат в одной плоскости. |
3.8. В плоскости (a, b) построить недостающую проекцию горизонтали h. |
||||
|
|
|
||||
3.9. Построить следы плоскости: а) (а, b), б) (f, h).
|
3.10. Определить углы наклона плоскости треугольника АВС к плоскостям проекций П1 и П2. Записать план решения задачи.
|
|
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
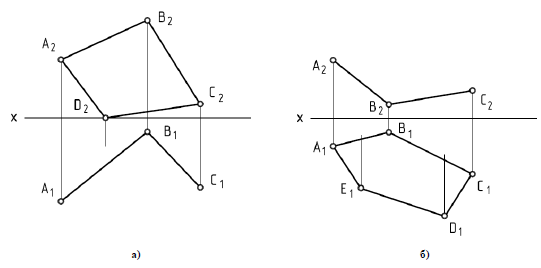
3.11. Достроить недостающую проекцию плоского многоугольника.
|
3.12. Построить проекции квадрата ABCD сторона которого ВС принадлежит прямой m и равна 1,5 стороны квадрата. Записать план решения задачи.
|
|
|
3.13. Построить проекции прямоугольного треугольника ABC, у которого катет BC принадлежит прямой m, угол B равен 90°, а гипотенуза А С равна 50 мм. |
3.14. Построить проекции равностороннего треугольника ABC плоскость которого наклонена к плоскости П2 под углом 45°. |
|
|
|
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
|
3.15. Построить проекции квадрата ABCD с вершиной А, принадлежащей прямой а, и диагональю BD, принадлежащей прямой m. Точка К - точка пересечения диагоналей. |
3.16. Построить проекции окружности с центром в точке О, радиусом 25 мм. Окружность расположена в плоскости (f, h). |
|
|
|
3.17. Построить линию пересечения плоскостей, заданных различными способами.
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
3.18. Построить линию пересечения плоскостей.
3.19. Построить линию пересечения плоскостей по стандартному алгоритму. Записать план решения задачи.
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
|
3.20. Построить линию пересечения плоскостей, заданных следами 2 и 2, и точке А, принадлежащей линии пересечения плоскостей. |
3.21. Построить линию пересечения плоскостей и , если точка А принадлежит линии пересечения плоскостей. |
|
|
|
3.22. Через точку А провести плоскость параллельную плоскости .
3.23. Проверить параллельность плоскостей.
|
3.24. Доказать параллельность плоскостей. |
3.25. Построить плоскость параллельную плоскости и отстоящую от нее на 25 мм. |
|
|
|
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
3.26. Найти точку пересечения прямой m с плоскостью для частных случаев расположения прямой или плоскости. Определить видимость.
г) д) е)
3.27. Найти точку пересечения прямой m с плоскостью . Определить видимость.
|
Выполнил студент |
________________________________ |
Группа |
__________________ |
|
3.28. Проверить параллельность прямой m и плоскости (А, n). |
3.29. Построить горизонтальную проекцию треугольника ABC, плоскость которого параллельна прямой m. |
|
|
|
