Тема 1. Матриці та визначники

Література: [1], с. 73-124; [2], с. 4-47; [3], с. 8-20; [7], с. 38-61; [9], с. 34-69.

1. Поняття матриці. Основні означення: матриця розмірності , матриця-рядок, матриця-стовпець, квадратна матриця, діагональна матриця, одинична матриця, нульова матриця.

2. Операції над матрицями: додавання та віднімання матриць, множення матриці на число, множення матриць, транспонування матриць.

Приклад 1. При яких значеннях сталих , , матриці ; рівні?

Приклад 2. Обчислити , , якщо

, , .

3. Визначники різних порядків, означення, властивості, обчислення.

Приклад. Обчислити визначники:

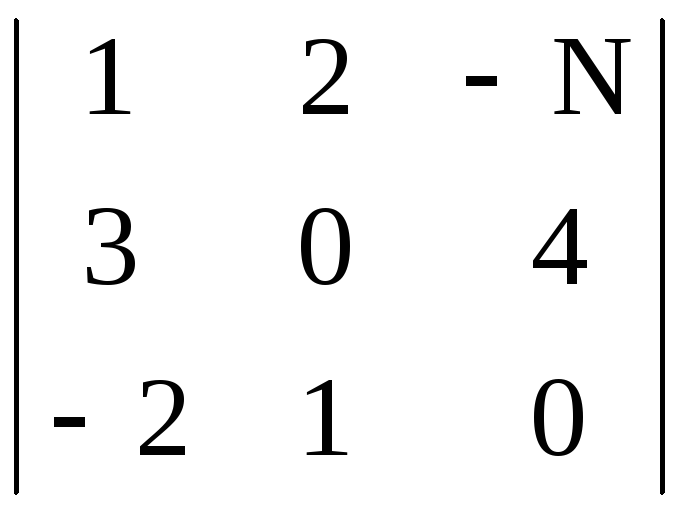а) ; б) ; в) ; г).

4. Оберненість матриць. Обчислення оберненої матриці.

Приклад. Обчислити матрицю, обернену до матриці .

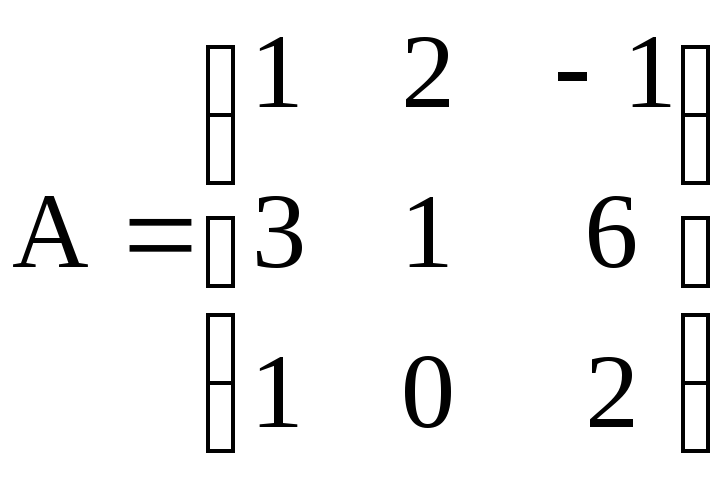Тема 2. Системи лінійних алгебраїчних рівнянь

Література: [1], с. 73-124; [2], с. 4-47; [3], с. 21-37; [7], с. 62-85; [9], с. 77-95.

1. Основні поняття і означення: система лінійних алгебраїчних рівнянь, розв’язок системи лінійних алгебраїчних рівнянь, сумісна та несумісна, визначена і невизначена система лінійних алгебраїчних рівнянь; еквівалентні системи.

2. Методи розв’язування систем лінійних алгебраїчних рівнянь: метод Крамера, матричний, Гаусса.

Приклад. Розв’язати систему лінійних алгебраїчних рівнянь:

а) за правилом Крамера; б) матричним методом; в) методом Гаусса.

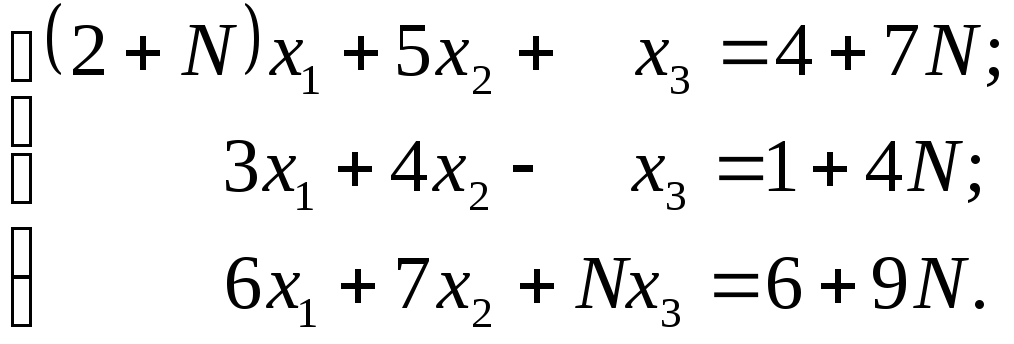
3. Теорема Кронекера-Капеллі. Однорідні системи.

Приклад. Дослідити систему лінійних алгебраїчних рівнянь на сумісність. У випадку сумісності знайти загальний та базисний розв’язки системи.

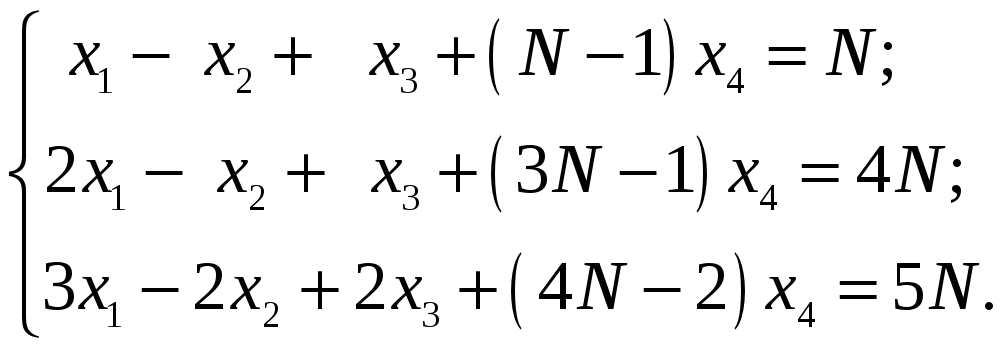
Розділ 2 Елементи векторної алгебри та аналітичної геометрії

Тема 3. Вектори та координати

Література: [1], с.73-124; [3], с. 54-64; [7], с.86-110; [9], с. 21-30.

1. Поняття вектора. Рівні, колінеарні, компланарні вектори. Орт вектора.

Вектори в ПДСК ( координати, довжина, напрямні косинуси).

Приклад. Побудувати вектори в системі координат:

а) , ;

б) , , .

Визначити орти векторів і . Вказати їх напрямні косинуси.

2. Лінійні операції над векторами: сума, різниця, добуток вектора на число в геометричному зображенні та координатах.

Приклад 1. При яких значеннях сталих та вектори

а) ; ;

б) ;

рівні: ?

Приклад 2. Обчислити ; , вектори , ; , , задані в пункті 1.

3. Скалярний добуток двох векторів: означення, властивості, обчислення, геометричний зміст, координатна форма.

Приклад 1. Визначити кут між векторами: і .

Приклад 2. При якому значенні сталої вектори , перпендикулярні?

4. Векторний добуток двох векторів: означення, властивості, обчислення, геометричний зміст, координатна форма.

Приклад 1. Обчислити векторний добуток векторів , та площу трикутника, побудованого на цих векторах.

Приклад 2. При яких значеннях сталих та вектори , колінеарні?

5. Мішаний добуток трьох векторів: означення, властивості, обчислення, геометричний зміст, координатна форма. „Ліва” та „права” трійка векторів.

Приклад 1. Для заданих векторів , , визначити:

а) мішаний добуток .

б) яку трійку векторів вони утворюють;

в) об’єм піраміди, побудованої на векторах , , .

Приклад 2. При якому значенні сталої вектори , , компланарні?