3. Властивості лінійно залежних та лінійно незалежних систем векторів.

1. Система векторів 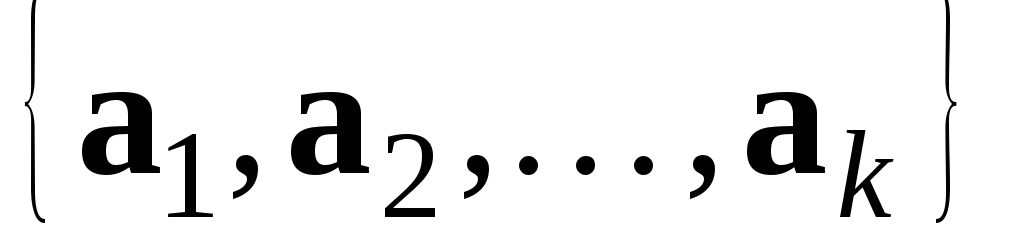, серед яких є нуль-вектор – лінійно залежна.

Доведення. Дійсно, нехай маємо систему векторів , причому . Розглянемо лінійну комбінацію з коефіцієнтами . Вона нетривіальна, проте, вочевидь, рівна нуль-вектору.

2. Критерій лінійної залежності векторів. Для того, щоб система векторів 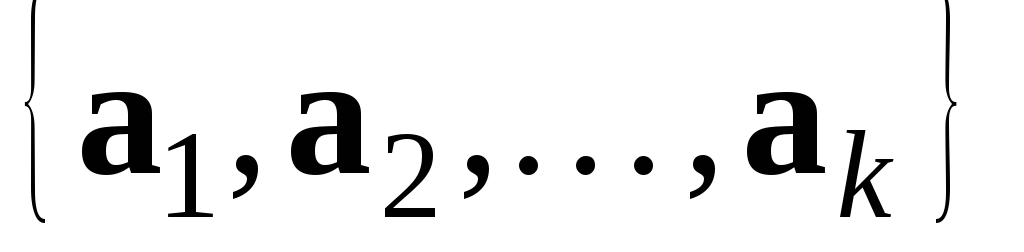була лінійно залежною, необхідно та достатньо, щоб принаймні один із векторів системи був лінійною комбінацією інших.

3. Якщо серед 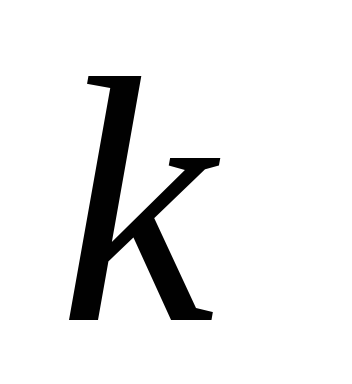векторів системи є лінійно залежна підсистема із яких-небудь 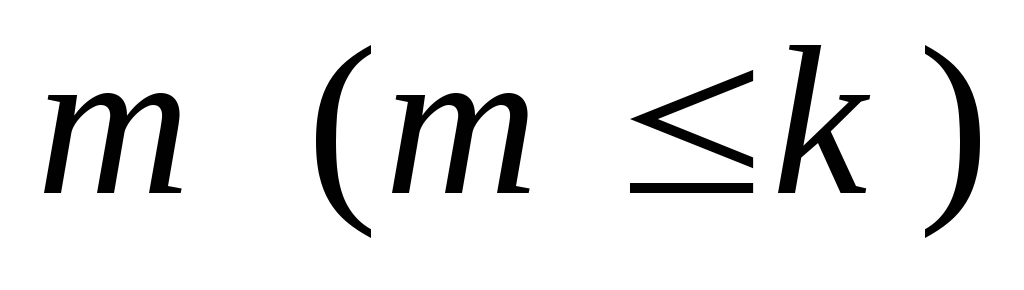векторів, то і вся система 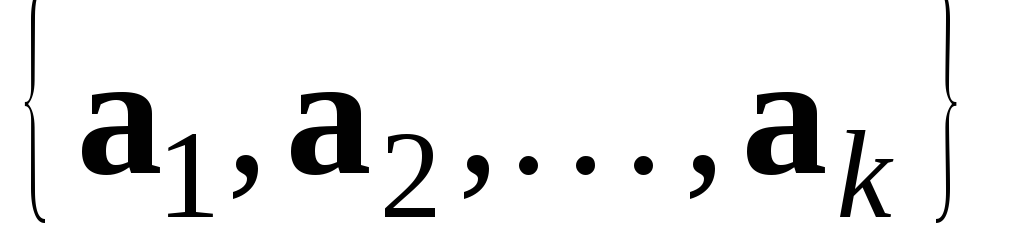– лінійно залежна.

4. Будь-яка підсистема векторів лінійно незалежної системи 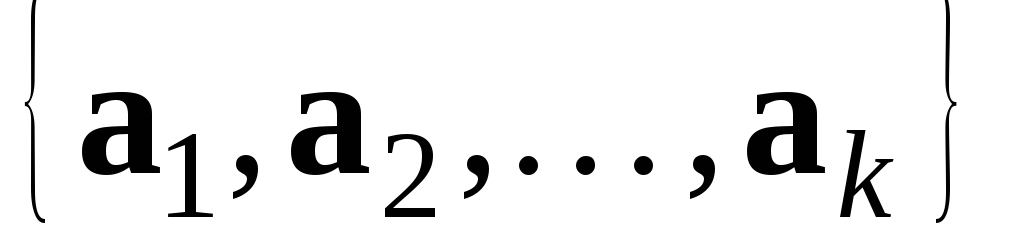– лінійно незалежна.

Означення 10. Векторний простір називається -вимірним, якщо в ньому існує лінійно незалежна система із векторів, а будь-які векторів утворюють лінійно залежну систему. Таким чином, число визначає вимірність простору.

Для підкреслення вимірності векторного простору будемо позначати його .

Приклади.

1. У просторі, що складається лише з нуль вектора, не існує лінійно незалежних векторів, тому вимірність цього простору рівна нулю.

2. Множина геометричних векторів, колінеарних фіксованому вектору 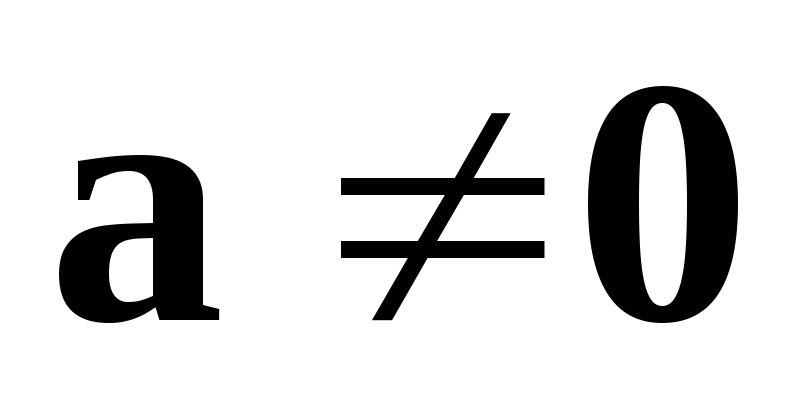, разом з нуль-вектором утворює одновимірний простір. Доведіть це самостійно.

3. Вимірність простору всіх геометричних векторів рівна 3. Адже вектори 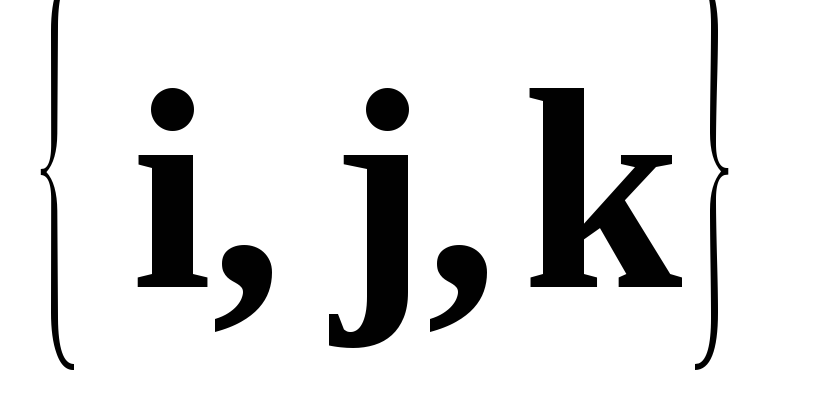декартової системи координат лінійно незалежні, а будь-який вектор може бути записаний у вигляді їх лінійної комбінації.

4. Множина поліномів порядку, що не перевищує 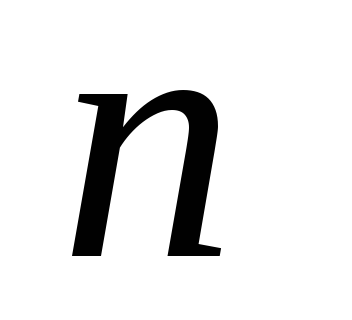, утворює простір вимірності 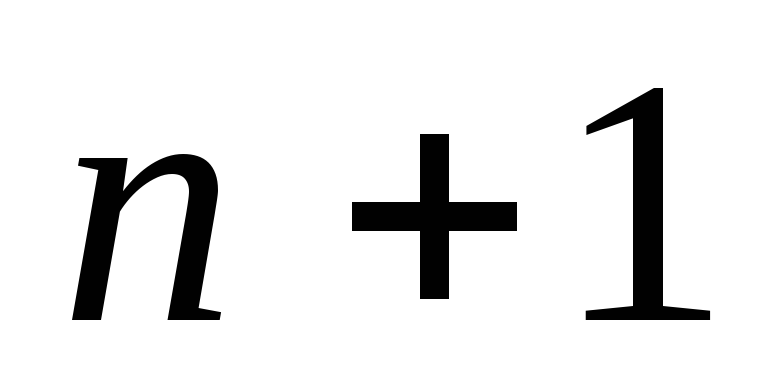. Дійсно 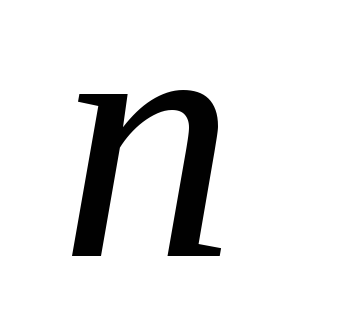поліномів 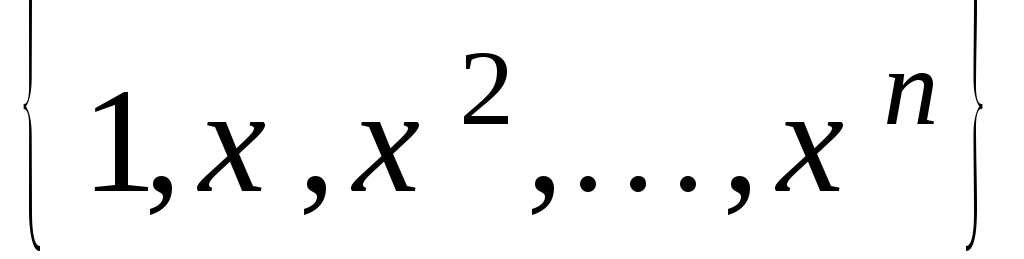утворюють лінійно-незалежну систему, а будь-який інший поліном порядку не більшого за 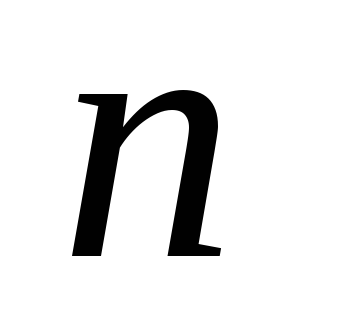, є їх лінійною комбінацією.

4. Базис скінчено вимірного векторного простору. Координати векторів.

Означення 12. Базисом -вимірного векторного простору називається довільна впорядкована лінійно незалежна система із векторів цього простору.

Зауваження 1. З означення випливає, що у векторному просторі існує безліч базисів.

Зауваження 2. Базис називають ще впорядкованою максимально лінійно незалежною системою векторів у просторі. Слово «максимально» тут означає, що до системи базисних векторів неможливо приєднати жодного вектору простору так, щоб система залишалась лінійно незалежною.

Теорема. Кожний вектор -вимірного векторного простору може бути поданий у вигляді лінійної комбінації векторів базису, причому таке подання єдине.

Означення 13. Якщо – базис векторного простору і – розклад деякого вектору по базису , то коефіцієнти цього розкладу називаються координатами вектора в базисі .

З доведеної вище теореми випливає, що будь-який вектор простору однозначно визначається своїм набором координат у вибраному базисі. Це дозволяє повністю абстрагуватись від самої природи векторного простору і мати справу лише з наборами координат замість векторів.

Зауваження. Координати вектора будемо записувати як вектор-стовпчик, позначаючи їх наступним чином: .

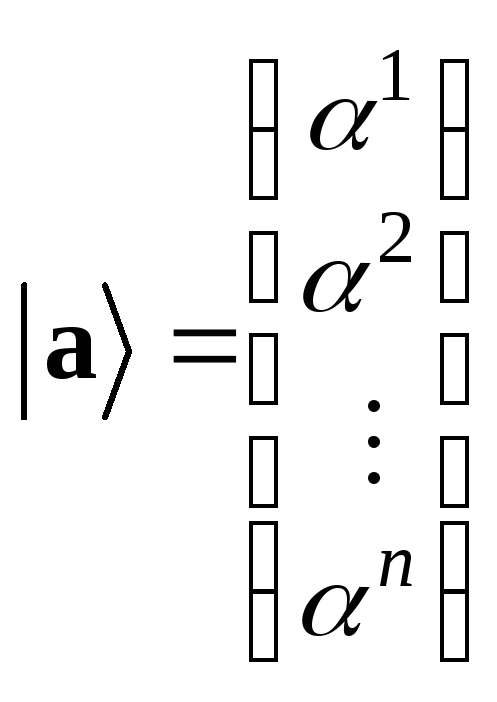Наслідки з теореми.

1. Координати будь-якого вектору простору у фіксованому базисі визначаються однозначно.

2. Два вектори рівні тоді і тільки тоді, коли рівні їх координати у фіксованому базисі.

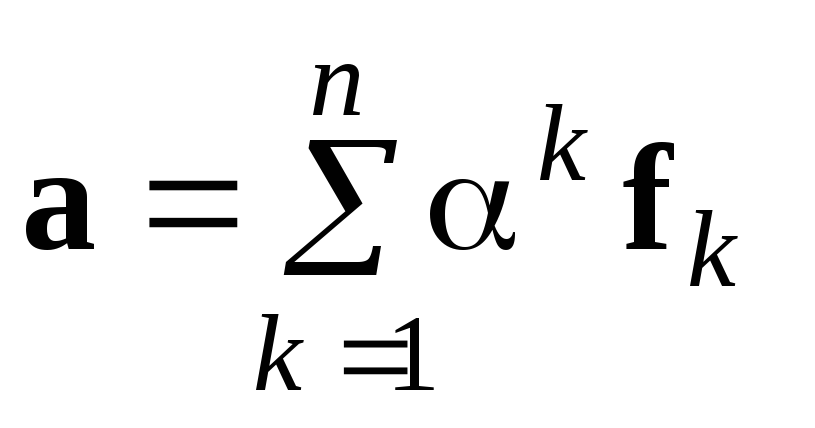3. Якщо та 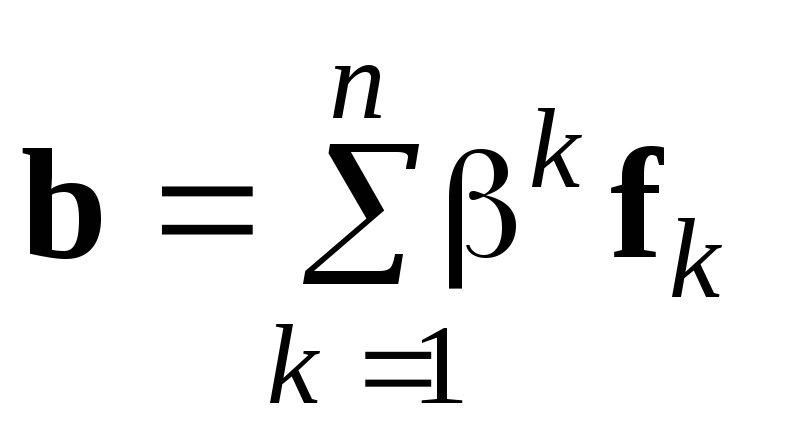розклади довільних векторів простру 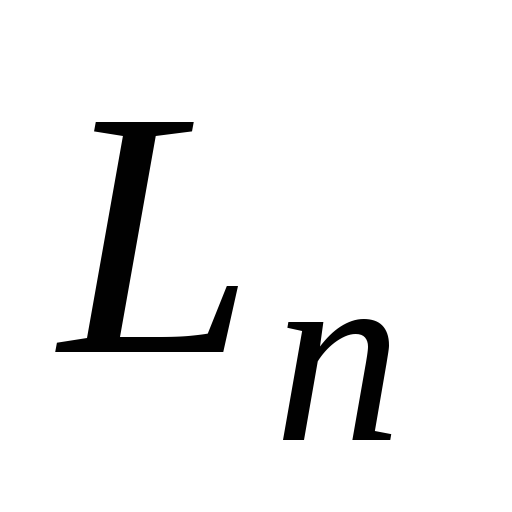по базису 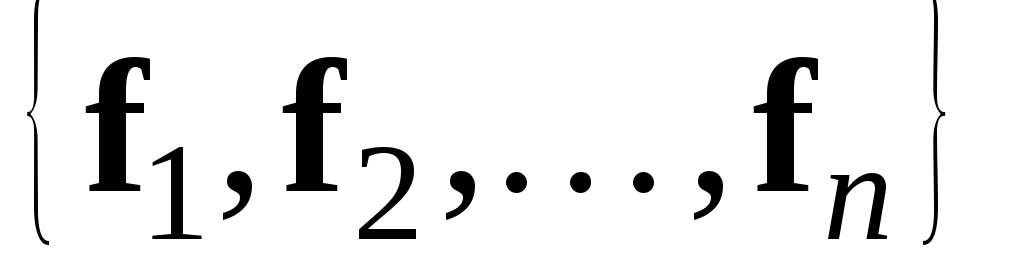, то вектор 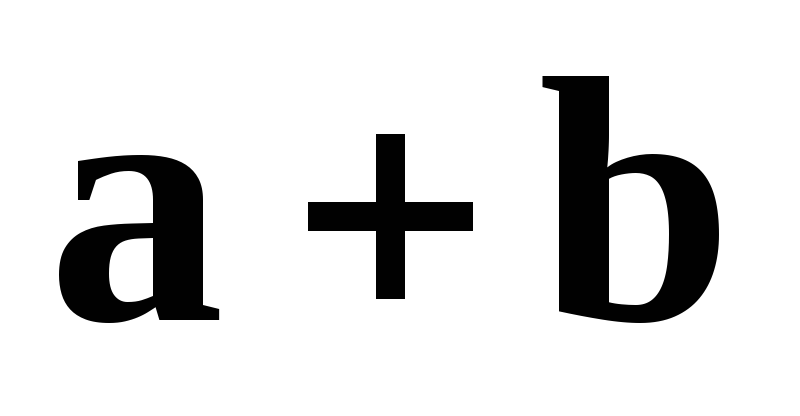в цьому базисі матиме координати 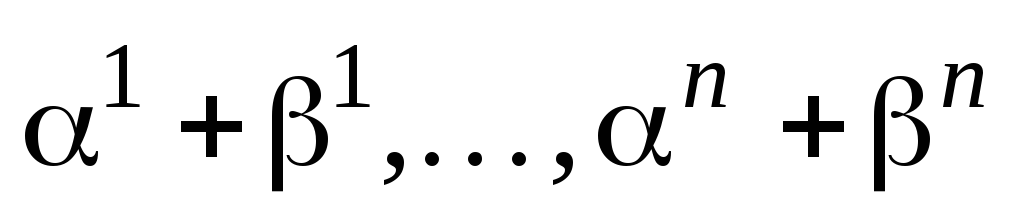, а вектор 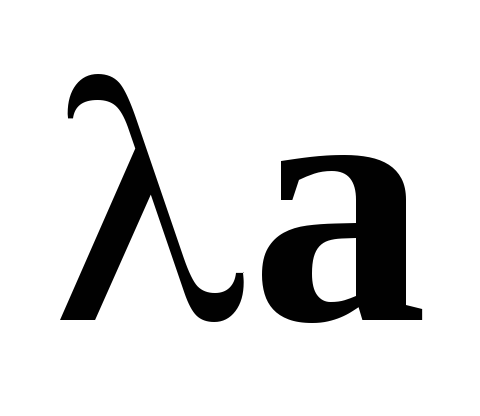– координати

. Доведіть цей факт самостійно.

4. Система векторів 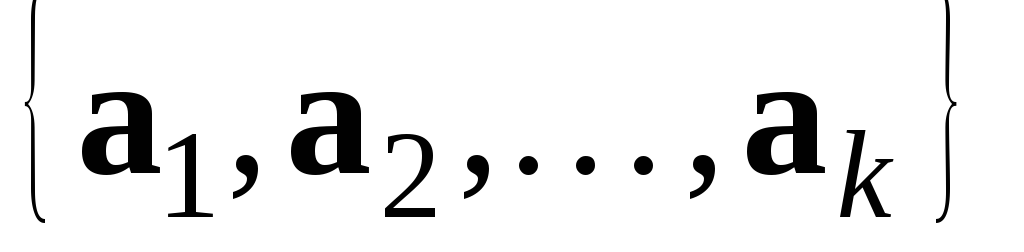простору 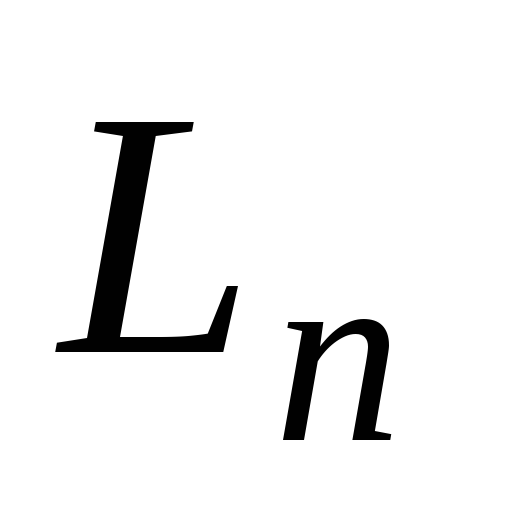лінійно незалежна тоді і тільки тоді, коли лінійно незалежна система вектор-стовпчиків їх координат. Доведіть це самостійно.