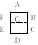1. Математические основы алгебры логики

ЦЕЛЬ: изучение основных понятий и определений алгебры логики и получение практических навыков формального преобразования аналитически заданных логических функций.

Формальное определение алгебры логики

Алгебра логики является теоретической основой проектирования современных цифровых автоматов и базируется на символической логике, предложенной математиком Джорджем Булем. Существует множество формальных определений булевых алгебр [1,2], зависящих от различных подходов к выбранной системе аксиом.

Булева алгебра может быть определена как алгебраическая система, удовлетворяющая следующим аксиомам [3].

Булевой алгеброй является система, состоящая из множества и двух типов операторов + и * (логическая сумма и логическое произведение), для которых справедливы следующие пять соотношений:

(коммутативность); (1)

(дистрибутивность); (2)

найдутся, такие, что

для любого (единичные элементы); (3)

найдется, такой, что для

любого (дополнение); (4)

(5)

с учетом того, что 1 > 0.

О

дним из вариантов булевой алгебры может служить алгебраическая система, в которой множество B содержит всего два элемента , которые одновременно являются единичным и нулевым элементами. При этом, соотношение (4) можно трактовать как введение дополнительной (третьей) логической операции, которую называют "отрицание" или "инверсия". Именно такую, самую простую, алгебраическую систему булевой алгебры, и принято называть в научно-технической литературе алгеброй логики, переключательной алгеброй, алгеброй релейно - контактных схем.

Алгебра логики в качестве аргументов использует логические переменные. Логические переменные и функции от них могут быть либо истинными (равными 1), либо ложными (равными 0). Логические переменные принято обозначать строчными латинскими буквами, а логические функции - прописными латинскими буквами.

В алгебре логики определены отношение эквивалентности (=) и три логические операции [4]: дизъюнкция (логическое сложение, операция ИЛИ); конъюнкция (логическое умножение, операция И); отрицание (инверсия, операция НЕ).

По аналогии с обычной алгеброй операцию ИЛИ обозначают в виде + или (знак дизъюнкции); операцию И обозначают *, или , или & (знак конъюнкции); операцию НЕ обозначают чертой над переменными или над значениями переменных, например, . Знак *, как и в обычной алгебре, чаще всего опускают (например, x * y = xy).

Отношение эквивалентности удовлетворяет следующим свойствам: x = x – рефлективность; если x = y, то y = x – симметричность; если x = y и y = z, то x = z – транзитивность. Из отношения эквивалентности следует принцип подстановки: если x = y, то в любой формуле, содержащей x, можно подставить y и будет получена эквивалентная формула.

Аксиомы алгебры логики

(6)

Аксиома (6) утверждает, что значения логических переменных и функций могут принимать всего два взаимоисключающих значения. Данную аксиому иногда называют "закон исключенного третьего". Следует помнить, что "1" и "0" - это не количественные характеристики, а качественные. Однако принимается, что 1 › 0.

(7)

Аксиома (7) определяет операцию дизъюнкции (логического сложения). Аксиома справедлива для любого числа слагаемых.

(8)

Аксиома (8) определяет операцию конъюнкции (логического умножения). Аксиома справедлива для любого числа сомножителей.

(9)

Аксиома (9) определяет операцию логического отрицания (инверсию).

В алгебре логики действует закон двойственности, который определяет соотношение между логической операцией «или», логической операцией «и» и логической операцией «не». Суть этого закона такова: если в уравнениях все переменные поменять на инверсные (противоположные) значения и заменить знак «ИЛИ» на знак «И» и наоборот, то получим эквивалентные уравнения.

Теоремы алгебры логики

Теоремы (10 - 19) легко доказываются с помощью аксиом (6-9) и метода подстановки возможных значений аргументов x.

Законы алгебры логики

Коммутативный закон (переместительный закон):

относительно логического сложения

x + y = y + x, (20 а)

относительно логического умножения

x * y = y * x . (20 б)

Данный закон гарантирует получение тождественного результата при перестановке местами аргументов.

Ассоциативный закон (сочетательный закон):

относительно логического сложения

x + y + z = y + (x + z) = (y + x) + z, (21 а)

относительно логического умножения

x * y * z = y * (x * z) = (y * x) * z. (21 б)

Данный закон позволяет при помощи скобок изменять порядок вычислений и гарантирует получение правильного результата, а также утверждает, что вычисление логической функции большого количества аргументов может быть сведено к последовательному ее вычислению суперпозицией функций двух аргументов.

Дистрибутивный закон (распределительный закон):

относительно логического сложения

x + (y * z) = (x + y) *( x + z), (22 а)

относительно логического умножения

x *(y + z) = (x * y) + ( x * z). (22 б)

Данный закон устанавливает правила раскрытия скобок относительно операций логического сложения и умножения.

Законы (правила) де Моргана:

(23 а)

(23 б)

Законы де Моргана определяют правила перехода от логической операции умножения к сложению (23 а) и наоборот (23 б).

Закон (23 а) утверждает, что отрицание конъюнкции, есть дизъюнкция отрицаний.

Закон (23 б) утверждает, что отрицание дизъюнкции, есть конъюнкция отрицаний.

Законы де Моргана называют также законами двойственности.

Как и в обычной алгебре в алгебре логики определен порядок выполнения логических операций: первой выполняется операция инверсии; второй - конъюнкции; третьей - дизъюнкции.

Табличная форма представления логических функций

Любую логическую функцию можно представить в табличной форме (таблицей истинности или картой Карно). Рассмотрим принцип построения таблиц истинности.

Таблица истинности — представление логической функции в виде таблицы. Таблица истинности содержит (n + k) столбцов и 2ⁿ строк, где n — число логических переменных, а k - число логических функций от n переменных.

В таблице истинности перечисляются (записываются) все возможные входные наборы логических переменных и

указываются значения логических функций на каждом из входных наборов логических переменных. Для того, чтобы правильно перечислить все возможные входные наборы логических переменных, можно придерживаться следующего правила заполнения таблицы истинности: все логические переменные, определяющие логическую функцию, номеруются (начиная справа) целыми числами j от 0 до n-1. Каждой логической переменной в таблице истинности, начиная сверху, присваивают чередующиеся группы значений (начиная с 0) через 2^j элементов в группе, где j - номер логической переменной (рис.5).

2n-1	2n-2		2j	22	21	20
xn-1	xn-2	xj		x2	x1	x0	y
a	b	………		z	p	q
				0	0	0
				0	0	1
				0	1	0
				0	1	1
				1	0	0
				1	0	1
				1	1	0
				1	1	1
…	…	…		…	…	…

Рис. 5. Пример заполнения таблицы истинности для одной логической функции n аргументов

Иными словами, для правильного заполнения таблицы истинности можно представить каждый входной набор значений логических переменных двоичным n-разрядным числом, и записать все возможные двоичные числа в порядке возрастания их значений, начиная со значения, равного нулю.

В правый крайний столбец (столбцы) таблицы истинности записываются значения логической функции.

В табл. 8 представлена в табличной форме логическая функция .

Таблица 8

Таблица истинности функции f

х2	х1	f
0	0	1
0	1	0
1	0	0
1	1	0

2. ПРОЕКТИРОВАНИЕ ЛОГИЧЕСКИХ СХЕМ С ПОМОЩЬЮ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Для формального синтеза комбинационных автоматов закон их функционирования должен быть описан каким-либо аналитическим способом. К таким аналитическим способам относят описание работы комбинационного автомата в виде совершенной дизъюнктивной нормальной формы (СДНФ) и совершенной конъюнктивной нормальной формы (СКНФ). Каждая логическая функция имеет одну СДНФ и одну СКНФ.

СДНФ логической функции называется дизъюнкция элементарных конъюнкций максимального ранга (n), соответствующих наборам из всех входных переменных, на которых значение логической функции равно 1.

СКНФ логической функции называется конъюнкция элементарных дизъюнкций максимального ранга (n), соответствующих наборам из всех входных переменных, на которых значение логической функции равно 0.

Ранг элементарной конъюнкции/дизъюнкции – это число входных переменных в элементарной конъюнкции/дизъюнкции.

Представление логических функций в виде дизъюнктивных и конъюнктивных нормальных форм называют структурными формулами, так как на их основе осуществляется формальный синтез структуры комбинационного автомата.

Логической схемой называется совокупность логических электронных элементов (рис. 6), соединенных между собой таким образом, чтобы выполнялся заданный закон функционирования схемы, иначе говоря, - выполнялась заданная логическая функция.

Рис. 6. Условное графическое обозначение основных логических элементов

ХОД ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ:

1. Используя законы, аксиомы и теоремы алгебры логики преобразовать аналитические выражения, задающие логические функции, так, чтобы в преобразованное аналитическое выражение входили только прямые и инверсные переменные (т.е., чтобы в аналитическом выражении отсутствовали “длинные” инверсии) (по варианту):

1.

2.

3.

4.

5.

6.

7.

8.

9. ;

10.

2. Построить таблицу истинности (ТИ) упрощенной логической функции.

3. Используя программу схемотехнического моделирования Electronics Workbench получить таблицу истинности исходной логической функции и сравнить ее с ТИ упрощенной логической функции.

4. Представить логическую функцию из табл. 9 в виде СДНФ И СКНФ (по варианту).

Таблица 9

x2	x1	x0	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9
0	0	0	1	1	0	0	1	1	0	1	1	1
0	0	1	0	1	1	0	1	1	1	1	0	0
0	1	0	0	0	0	0	0	1	1	1	1	1
0	1	1	1	1	1	1	0	0	1	1	1	1
1	0	0	0	0	0	0	1	1	0	0	0	0
1	0	1	1	0	1	0	1	0	1	0	1	0
1	1	0	0	1	0	1	0	1	0	1	1	0
1	1	1	1	0	1	0	1	1	1	0	1	1

5. С помощью программы схемотехнического моделирования Electronics Workbench (EWB) построить логические схемы логических функций, заданных в СДНФ и СКНФ, используя логические элементы И, ИЛИ, НЕ, и проверить закон их функционирования c помощью логического конвертера программы EWB.

Лабораторная работа №3

МЕТОД МИНИМИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ С ПОМОЩЬЮ КАРТ КАРНО

ЦЕЛЬЮ минимизации логических функций является получение более простых аналитических выражений, что в свою очередь позволяет осуществлять более простую минимизацию синтезируемого автомата.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1. Метод минимизации полностью определенных логических функций с помощью карт Карно.

Метод минимизации логических функций с помощью карт Карно заключается в следующем: на карту Карно наносятся единичные и нулевые значения логических функций. Для получения ДНФ логической функции рассматриваются единичные значения функции, а для получения КНФ – нулевые [4].

Пусть с помощью карты Карно задана логическая функция , необходимо найти ее тупиковую ДНФ. Тогда задача минимизации решается следующим образом: среди единичных значений логической функции , предварительно нанесенных на карту Карно, отыскиваются прямоугольники и/или квадраты с числом клеток , где k=(n-1),…,0. Выделяемые прямоугольники и/или квадраты могут пересекаться между собой.

Задача минимизации состоит в том, чтобы все единичные значения логической функции покрыть минимальным количеством прямоугольников и/или квадратов максимальной площади, величина которых должна быть кратна .

Тупиковой дизъюнктивной нормальной формой логической функции называется такая ДНФ, реализующая , в которой ни одна из импликант не является лишней, то есть ни одна из импликант не может быть удалена из формулы.

Импликанты – это элементарные конъюнкции ранга меньше максимального, которые не могут быть склеены (т.е. объединены) между собой.

Для формирования тупиковых ДНФ в каждом прямоугольнике и/или квадрате находится соответствующая импликанта, которая является одинаковой для всех объединенных клеток карты Карно. Найденные из каждого прямоугольника и/или квадрата импликанты соединяются знаком дизъюнкции.

Если необходимо найти тупиковую КНФ логической функции , то задача минимизации решается следующим образом: среди нулевых значений логической функции , предварительно нанесенных на карту Карно, отыскиваются прямоугольники и/или квадраты с числом клеток , где k=(n-1),…,0. Выделяемые прямоугольники и/или квадраты могут пересекаться между собой.

Задача минимизации состоит в том, чтобы все нулевые значения логической функции покрыть минимальным количеством прямоугольников и/или квадратов максимальной площади, величина которых должна быть кратна .

Для формирования тупиковых КНФ в каждом прямоугольнике и/или квадрате находят элементарные дизъюнкции логических переменных, которые являются общими для всех выделенных клеток карты Карно. Найденные из каждого прямоугольника и/или квадрата дизъюнкции соединяются знаком конъюнкции.

При применении метода минимизации логических функций с помощью карт Карно необходимо помнить о том, что карты Карно обладают свойством цилиндричности, т.е. клетки, расположенные по краям карт Карно являются соседними в каждом столбце и каждой строке и могут объединяться в прямоугольники и/или квадраты.

2. Метод минимизации частично определенных логических функций с помощью карт Карно

Для минимизации частично определенных булевых функций необходимо доопределить карты Карно, которыми эти функции заданы. Доопределяем функции единичными и нулевыми значениями так, чтобы при составлении ДНФ было минимальное количество импликант наименьшего ранга, то есть покрываем все единичные значения прямоугольниками и/или квадратами максимальной площади, при этом число прямоугольников и/или квадратов должно быть минимальным.

3. Способ Шеннона оценки эффективности минимизации форм логических функций.

Сравнение эффективности минимизированных форм часто проводят по способу Шеннона. Этот способ базируется на введении такого понятия как цена схемы – Ц. Цену схемы можно рассчитать по следующей формуле:

, (24)

где - количество входов у j-ого элемента, i-количество элементов.

Пусть логическая функция R(a,b,c,d) задана в виде СДНФ (25 а):

(25 а)

Минимизированная ДНФ логической функции R(a,b,c,d) имеет вид:

(25 б)

Оценим аналитическое выражение (25 б) по формуле (24). Элементов “И” в выражении присутствует 5 (два элемента “И” по 2 входа, три элемента “И” по 3 входа), элементов “ИЛИ”- 1 (один элемент на 5 входов), элементов “НЕ”- 4 (4 элемента по 1 входу), следовательно:

Ц=2*2+3*3+1*5+4*1=22 входа

Тем же способом оценим СДНФ логической функции R(a,b,c,d) – выражение (25 а):

Элементов “И” - 11 (одиннадцать элементов по 4 входа), элементов “ИЛИ”- 1 (один элемент на 11 входов), элементов “НЕ”- 4 (4 элемента по 1 входу), следовательно:

Ц=11*4+1*11+4*1=59 входов

ХОД ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ:

Логические функции F_i (a, b, c ,d), где i=1,…10, заданы таблицей истинности (табл.10). В ходе данной лабораторной работы необходимо:

1. Рациональным образом доопределить представленные в табл. 10 логические функции и минимизировать их методом карт Карно.

2. Произвести минимизацию логических функций из табл.10 с помощью программы схемотехнического моделирования Electronics Workbench.

3. Сравнить полученные в ходе минимизации результаты и выяснить, совпадают ли полученные тупиковые ДНФ логических функций, найденные методом карт Карно и формы, полученные с помощью программы схемотехнического моделирования EWB и в случае их расхождения выявить причины.

4. Для любых двух логических функций из табл. 10 оценить ее СДНФ и полученную в лабораторной работе тупиковую ДНФ по способу Шеннона.

5. Для этих же логических функций по табл.10 выписать их СКНФ и методом минимизации с помощью карт Карно получить их тупиковые КНФ. Правильность получения форм проверить с помощью логического конвертера в программе схемотехнического моделирования Electronics Workbench .

Таблица 10

a	b	c	d	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10
0	0	0	0	-	1	0	1	1	1	-	-	0	0
0	0	0	1	0	0	1	-	0	0	1	1	1	-
0	0	1	0	1	-	1	0	0	-	1	1	0	0
0	0	1	1	-	-	-	1	1	0	-	-	-	1
0	1	0	0	1	0	1	1	1	1	0	1	-	1
0	1	0	1	1	1	1	-	-	1	-	1	1	0
0	1	1	0	-	1	0	0	-	0	1	0	0	1
0	1	1	1	0	-	0	0	1	0	0	0	1	-
1	0	0	0	0	1	-	1	0	-	1	-	1	0
1	0	0	1	-	0	1	1	1	-	1	0	1	1
1	0	1	0	1	1	0	-	0	1	0	1	-	-
1	0	1	1	0	1	0	0	-	0	1	0	0	1
1	1	0	0	1	1	0	1	0	0	0	0	1	-
1	1	0	1	-	0	1	-	1	1	0	0	-	0
1	1	1	0	0	0	0	1	1	1	1	-	1	1
1	1	1	1	1	0	1	0	-	-	1	0	0	0

Лабораторная работа №4

СИНТЕЗ И МОДЕЛИРОВАНИЕ ПРЕОБРАЗОВАТЕЛЯ ДВОИЧНО-ДЕСЯТИЧНОГО КОДА В СЕМИСЕГМЕНТНЫЙ КОД

ЦЕЛЬ: закрепление теоретических положений теории автоматов и получение практических навыков по формальному синтезу преобразователя двоично-десятичного кода в семисегментный код.

ЗАДАНИЕ: требуется синтезировать преобразователь двоично-десятичного кода в семисегментный код, на вход которого поступают входные сигналы , , , и который формирует семь выходных сигналов А, В, С, D, E, F, G (рис.8), которые управляют свечением семисегментного индикатора (рис.9):

Рис. 8. Структурная схема преобразователя двоично-десятичного кода в семисегментный код на уровне черного ящика.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Семисегментные индикаторы относятся к выходным устройствам для индикации цифровой информации. Семь сегментов индикатора обозначены на рис. 9 а буквами А, В, С, D, E, F, G. Каждый из сегментов может светиться или не светиться. В зависимости от того, какая группа сегментов светится, можно получить изображение десятичных цифр 0, 1, 2, ..., 9 (рис. 9 б). Исходными сигналами, представляющими десятичные цифры, являются обычно двоично-десятичные коды. Поэтому для обеспечения функционирования семисегментного индикатора необходимо преобразовать двоично-десятичный код в семисегментный код, представляющий собой семиразрядное слово, составленное из логических нулей и единиц [5].

Рис.9. Обозначение сегментов (а) и цифры, высвечиваемые на семисегментном индикаторе (б)

1. Построение таблицы истинности преобразователя

Для того, чтобы построить схему преобразователя, необходимо составить таблицу истинности (табл. 11), которая описывает работу данного преобразователя. Для составления таблицы истинности будем использовать рис. 9. Предполагается, что активным уровнем, вызывающим свечение элементов индикатора, является логическая единица.

Таблица 11

i	Входы				Индикаторы	Выходы
						A	B	C	D	E	F	G
0	0	0	0	0		1	1	1	1	1	1	0
1	0	0	0	1		0	1	1	0	0	0	0
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
					Продолжение табл. 11
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1

Значения выходных сигналов А, В, С, D, E, F, G заполняются в соответствии со свечением определенных сегментов индикатора, отображающего десятичные цифры 0, 1, 2, ..., 9. Если сегмент индикатора, отображающий ту или иную цифру должен светиться, то выходной сигнал равен 1, если нет – то 0. Например, при отображении цифры 1 светятся только два сегмента В и С, следовательно B=1, С=1, а А, D, E, F, G равны 0.

При составлении таблицы истинности необходимо учитывать, что наборы никогда не используются и поэтому выходные сигналы на этих наборах могут принимать любые значения.

2. Преобразование части схемы в подсхему

Electronics Workbench позволяет объединять участки схемы в подсхемы (субблоки). Для этого необходимо выделить участок схемы, который нужно объединить в подсхему. Выделяемая часть схемы должна быть расположена таким образом, чтобы в выделенную область не попали не относящиеся к ней проводники и компоненты. После выделения нужно выбрать пункт Create Subcircuit меню Circuit. В результате выполнения команды открывается диалоговое окно (рис. 10), в строке Name которого вводится имя подсхемы (без пробела), после чего возможны следующие варианты: Сору from Circuit — подсхема копируется с указанным названием в библиотеку Custom без внесения изменений в исходную схему; Move from Circuit — выделенная часть вырезается из общей схемы и в виде подсхемы с присвоенным ей именем копируется в библиотеку Custom; Replace in Circuit — выделенная часть заменяется в исходной схеме подсхемой с присвоенным ей именем с одновременным копированием ее в библиотеку Custom [6]. Для выполнения лабораторной работы необходимо выбрать пункт Replace in Circuit.

Рис. 10. Диалоговое окно Create Subcircuit

3. Работа с подсхемой

Для просмотра или редактирования подсхемы нужно дважды щелкнуть мышью по ее значку. Редактирование подсхемы производится по общим правилам редактирования схем. При создании дополнительного вывода подсхемы необходимо из соответствующей точки подсхемы курсором мыши протянуть проводник к краю окна подсхемы до появления не закрашенной прямоугольной контактной площадки, после чего отпустить левую кнопку мыши. Для удаления вывода необходимо курсором мыши ухватиться за его прямоугольную площадку у края окна подсхемы и вынести ее за пределы окна.

4. Проверка правильности функционирования синтезированного преобразователя двоичного кода в семисегментный код.

Для проверки правильности функционирования преобразователя необходимо последовательно подавать на его входы наборы значений входных переменных. Для этого входы схемы необходимо подключить к генератору слов (рис. 11), представленному в разделе Instruments. Самый крайний правый выход генератора слов подключается к логической переменной (), отвечающей за младший разряд входного набора значений логических переменных. Далее в соответствии с разрядами подключаются входы , , .

Вход внешней синхронизации

Выход тактового сигнала

Рис. 11. Уменьшенное изображение генератора слов

Щелкнув два раза левой кнопкой мыши по изображению генератора слов в расширенном изображении генератора слов найти вкладку PATTEM, выбрать пункт UP COUNTER (счетчик), затем нажать кнопку ACCEPT. Далее выбрать пошаговый режим работы, нажав кнопку STEP.

Выход преобразователя необходимо подключить к семисегментному индикатору (рис. 12), расположенному в разделе Indicators. Это позволит провести проверку правильности работы синтезированной схемы преобразователя. Каждый из семи выводов индикатора управляет соответствующим сегментом А, В, С, D, E, F, G. При поступлении на его входы сигналов А, В, С, D, E, F, G индикатор будет отображать десятичные числа от 0 до 9, в соответствии с табл.11.

Рис.12. Семисегментный индикатор

После подключения входов и выходов схемы необходимо включить режим моделирования работы преобразователя, нажав на кнопку “1”, расположенную в верхней правой части окна программы EWB.

ХОД ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ:

1. Составить таблицу истинности работы преобразователя двоично-десятичного кода в семисегментный код.

2. Произвести доопределение таблицы истинности преобразователя и минимизировать логические функции А, В, С, D, E, F, G с помощью карт Карно или программы схемотехнического моделирования EWB.

3. Получить структурные формулы, задающие закон функционирования преобразователя в виде дизъюнктивной нормальной формы (ДНФ) или в конъюнктивной нормальной форме (КНФ) (выбрать более выгодную для последующей реализации структурную формулу).

4. По полученным формулам построить логические схемы в пакете EWB, формирующие выходные сигналы А, В, С, D, E, F, G. Каждую из схем оформить в виде в виде подсхемы.

5. Из полученных подсхем, реализующих выходные сигналы А, В, С, D, E, F, G, построить схему логического преобразователя.

6. Проверить правильность работы преобразователя двоично-десятичного кода в семисегментный код с помощью программы схемотехнического моделирования EWB.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Сикорский Р. Булевы алгебры / Р. Сикорский. М.: Мир, 1969. 376 с.

2. Яглом И.М. Булева структура и ее модели. / И.М. Яглом. М.: Сов. радио, 1980. 192 с.

3. Киносита К. Логическое проектирование СБИС / К. Киносита, К. Асада, О. Карацу. М.: Мир, 1988. 309 с.

4. Тюрин С.В. Элементы теории автоматов (часть 1): учеб. пособие / С.В. Тюрин. Воронеж: ВГТУ, 2002. 98 с.

5. Новожилов О.П. Основы цифровой техники: учеб. пособие / О.П. Новожилов. М.: ИП РадиоСофт, 2004. 528 с.

6. Кардашев Г.А. Цифровая электроника на персональном компьютере. Electronics Work bench и Micro-Cap/ Г.А. Кардашев. М.: Горячая линия-Телеком, 2003. 311 с.