
-
Общие индексы
Общие индексы показывают соотношение совокупности явлений, состоящих из разнородных, непосредственно несоизмеримых элементов.
Общие индексы обозначаются символом (І).
Агрегатными называются индексы, числители и знаменатели дробей которых представляют собой соединения сумм, произведений или суммы произведений уровней изучаемого явления.
Эта форма индексов является основной.
Рассмотрим построение общих индексов на следующем примере: предприятия выпускает n наименований различной продукции, в базисном периоде было реализовано (продано) q0i - количество продукции і-ого наименования по цене р0i, а отчётном периоде – соответственно q1i и р1i.
Стоимость реализованной продукции предприятия в отчетном периоде составила:
- по ценам отчётного периода - Σ р1· q1 ;
- по ценам базисного периода - Σ р0· q1 .
Стоимость реализованной продукции предприятия в отчетном периоде составила:
- по ценам отчётного периода - Σ р1· q0
- по ценам базисного периода - Σ р0· q0 .
Общий индекс товарооборота (реализованной продукции):
![]() .
(1.2)
.
(1.2)
Агрегатная формула индекса реализованной продукции показывает, что его величина зависит от двух явлений, от двух переменных величин – от количества реализованной продукции и цен за каждую единицу реализованной продукции.
Чтобы выявить влияние каждой переменной в отдельности следует исключить влияние одной из них, т.е. принять её условно в качестве постоянной, неизменной величины на уровне отчётного или базисного периода.
В этой связи возникает вопрос о базисных и отчётных весах агрегатного индекса. Рассмотрим этот вопрос на примере индекса цен и индекса физического объёма продукции.
Общее изменение цен можно определить при условии, если в качестве постоянной, неизменной величины взять количество проданных товаров за отчётный или базисный период.
-
Если для получения индекса цен принять в качестве весов данные о количестве реализованной продукции за отчётный период, формула агрегатного индекса цен будет иметь вид:
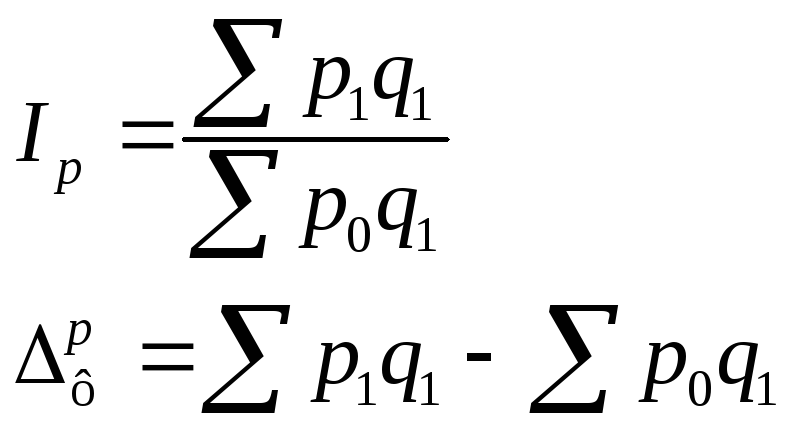 .
(1.3)
.
(1.3)
Этот индекс
характеризует изменение цен отчётного
периода по сравнению с базисным по
продукции, реализованной в отчётном
периоде, и фактическую
экономию от снижения цен
(![]() ).
).
-
Если же принять в качестве весов данные о количестве реализованной продукции в базисном периоде, формула агрегатного индекса цен будет иметь вид:
![]() .
(1.4)
.
(1.4)
Этот индекс показывает насколько изменились цены в отчётном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде, и экономию, которую можно было бы получить от снижения цен, т.е. условную экономию.
Правильно отражает динамику изменения цен агрегатный индекс цен с отчётными весами.
Агрегатный индекс физического объема продукции должен отражать изменение физического объёма в отчётном периоде по сравнению с базисным.
Сомножитель индексируемого показателя берется на уровне базисного периода (р0):
![]() (1.5)
(1.5)
![]() -
абсолютное изменение
физического объёма.
-
абсолютное изменение
физического объёма.
Выбор периодов взвешивания индексов зависит от того, какие индексы вычисляются: индексы объёмных (количественных) или качественных показателей.
В теории статистики принята следующая система взвешивания:
- сомножители количественных индексируемых показателей берутся на уровне базисного периода;
- сомножители качественных индексируемых показателей - на уровне отчётного периода.
В рассмотренном примере количество реализуемой продукции – количественный показатель, а цена – качественный.
Индекс себестоимости продукции показывает фактическую себестоимость в отчётном периоде по сравнению с базисным:
![]() .
(1.6)
.
(1.6)
Индекс трудоёмкости характеризует изменение трудоемкости единиц продукции в отчётном периоде по сравнению с базисным (является индексом качественного показателя):
![]() .
(1.7)
.
(1.7)
Индекс
производительности труда
(производительность труда определяется
количеством продукции, производимой в
единицу времени -
![]() )
характеризует изменение производительности
труда в отчётном периоде по сравнению
с базисным:
)
характеризует изменение производительности
труда в отчётном периоде по сравнению
с базисным:
![]() .
(1.8)
.
(1.8)
Агрегатный индекс может быть вычислен при помощи индивидуальных индексов, потому что всякий общий индекс является средневзвешенным из индивидуальных индексов.
Пример: известно q0 · p0 и iq , необходимо определить общий индекс физического объема продукции.
Индивидуальный индекс физического объёма продукции:
![]() ,
,
откуда q1=iq· q0 .
Среднеарифметический индекс физического объема продукции определится по формуле:
![]() .
.
Пример: известно q1 · p1 и ip, необходимо определить общий индекс цен.
Из формулы индивидуального индекса цен получим:
![]() .
.
В итоге получим формулу для расчета среднегармонического индекса физического объёма продукции:
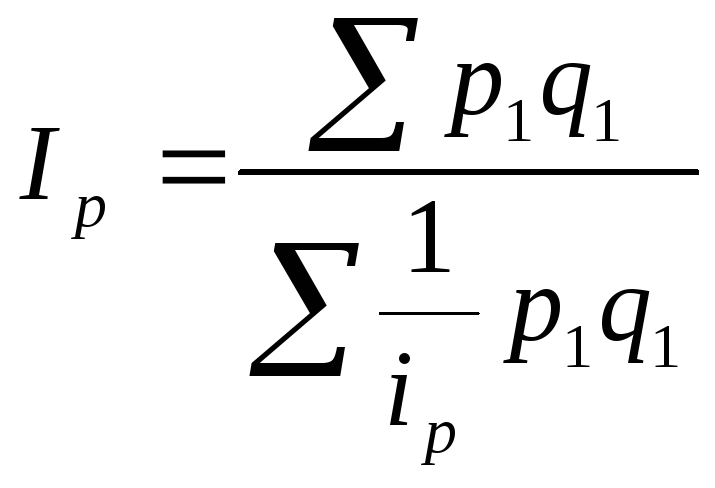 .
.
