Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

удобно использовать функцию polyroots. Пример записи решения приведен на рис. 11.

Рис.11. Примеры отыскания корней полинома

Сначала формируется вектор коэффициентов а_к, начиная с а₀. Затем выполняется команда polyroots. Второй пример отыскивает корни уравнения, приведенного на рис. 10б.

Функция polyroots удобна тем, что не требуется первого приближения.

Работа с комплексными числами

MathCAD воспринимает комплексное число как a + bi, где а – вещественная часть, b – мнимая. Если привычнее использовать j вместо i, вызовите меню Формат, в нем Формат результата, далее Параметры экрана, и в нем Мнимое значение, в котором вызываете символ j. Тогда комплексное число будет восприниматься как a + b j. Следует иметь в виду, что символы i или j можно ставить только непосредственно после числа, например, 6 j. Если необходимо ввести мнимую единицу, необходимо печатать 1i или 1j. Когда курсор покидает выражение, единица пропадает. Мнимую единицу можно также получить как . В этом случае j воспринимается как переменная.

Задавать комплексное число можно также в показательной форме как, например, Zе^j, где  угол вектора . Но результат всегда выдается как a + bi.

В MathCAD кроме арифметических операций имеются специальные функции и оператора для работы с комплексными числами:

Re (Z) ­– выделяет вещественную часть комплексного числа (вектора );

Im (Z) – выделяет мнимую часть комплексного числа (вектора );

arg(Z) – определяет угол вектора ;

|Z| – определяет модули вектора ;

– выполняет сопряжение вектора (изменяет знак мнимой части).

Операции с комплексными числами приведены на рис. 12.

Р ис. 12. Примеры действия с комплексными числами.

Построение графиков

Начиная с первого курса, студенты постигают математические функции и зависимости через графические их представление. В системе MathCAD имеется возможность построить графики самого различного вида.

Рассмотрим табличную зависимость двух параметров y = f(x).

x	0	1	2	3	4
y	0	1	1.5	1.7	1.8

Зададим х и у векторами, т.е. матрицами-столбцами.

Чтобы построить график этой функции, достаточно в панели вывода палитр математических знаков вызвать палитру Graph и выбрать кнопку графика двух параметров. Появится пустой график с двумя полями ввода по одному на каждой оси. Если в нижнее поле ввода занесем х, а в левое – у, получим искомую зависимость (левый график).

Однако этот график не совсем удобный. Он мал по площади, на нем отсутствует сетка. Увеличить масштаб можно, щелкнув по графику мышкой. График оконтурится черной рамкой с тремя квадратиками на ней – справа, снизу и в правом нижнем углу. Установив курсор на одном из квадратиков, и двигая мышкой, можно растянуть график вправо, вниз и одновременно вниз и вправо.

Если два раза щелкнуть на графике, вызовется панель форматирования графика, приведенная на рис 14. В колонках Ось – Х и Ось – Y птичками отмечены Нумерация, Автомасштаб, Авто сетка. Отметим еще Вспомогательные линии и после нажатия на кнопку ОК получим правый график (рис. 13). Чтобы изменить масштаб, выключите Авто сетку, а в окна Размер сетки внесите нужные масштабы. Пример приведен на рис 14.

Рис. 13, 14. Примеры построения графиков, заданного таблично.

Рассмотрим пример построения потенциальной диаграммы для задачи, приведенной на рис 7. Для большей наглядности ЭДС Е₂ перенесена и включена между сопротивлениями R₂ и R₃. На рис. 15. приведено решение задачи. Токи в ветвях определены через уравнения Кирхгофа. Потенциалы точек и нарастающее сопротивление от точки а по внешнему контуру по часовой стрелке представлены векторами  и R. Отличие от предыдущих графиков в использовании формата Показать метки для выделения горизонтальной осевой линии. Тот же результат можно получить, если в Стиле осей графика отметить Пересечение. Фиксированные точки отмечены крестиками, которые получены, открыв Трассировку, а затем через Символ.

Рис. 15. Построение потенциальной диаграммы в цепи постоянного тока.

Используя палитру Graph, можно построить векторы, заданные комплексными числами. Построим векторную диаграмму трехфазной системы напряжений. (рис.16). Напряжения U_A, U_B, U_C заданы в показательной форме. Далее представим напряжения в виде векторов (матрицами-столбцами). Первый член матрицы равен нулю, второй - фазному напряжению. Вызовем палитру Graph, вызовем кнопкой график в декартовых координатах и по вертикальной оси через запятую занесем активные составляющие векторов, по горизонтальной – реактивные. В Стиле осей графика нажмем кнопку «Пересечение», а справа отметим Равные масштабы. Размер сетки принят равным 10. Следует отметить , что обязательно при построении векторных диаграмм следует строить сетку, потому что даже при фиксировании Равных масштабов они зачастую равными не получаются, и приходится вручную изменять размеры графика по горизонтали или по вертикали. При построении графика, изображенного на рис. 16 так и получилось.

Первая переменная всегда окрашивается в красный цвет, вторая – в синий, третья – в зеленый. Если Вам необходимо изменить цвета, вызовите Трассировку и измените цвет. Здесь же можно изменить толщину линий, задать их пунктирными, точками, пунктирными с точками и др.

Кроме векторных диаграмм на графике можно построить топографическую диаграмму, а также суммировать или вычитать векторы. Чтобы суммировать или вычесть векторы, в матрице-столбце последний член задать равным нулю. Примеры топографической диаграммы и вычитания векторов приведены на рис. 17.

Р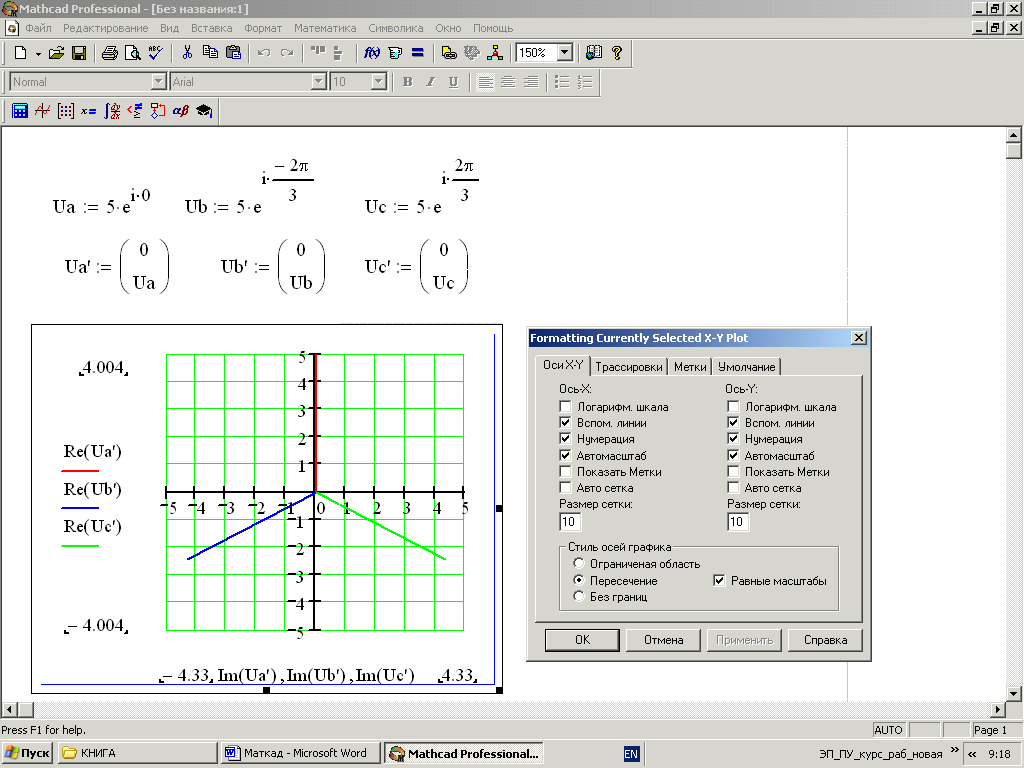 ис. 16. Векторная диаграмма трехфазной системы напряжений

Р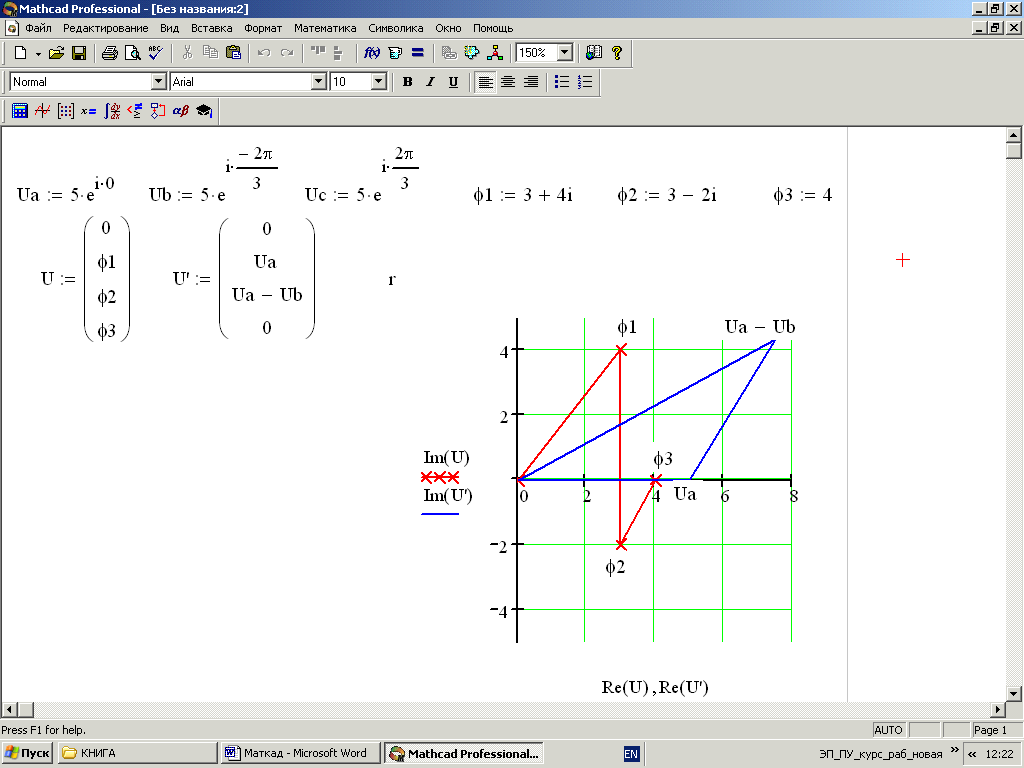 ис. 17. Примеры топографической диаграммы и вычитания векторов

Рассмотрим построение графика функции от какого-либо аргумента, изменяющегося монотонно. Например, и . Пример построения графика приведен на рис 18. В первую очередь необходимо задать значение угловой частоты  и интервал времени. Интервал времени задается начальным моментом (в нашем примере нулем), затем задается следующий момент времени, затем команда многоточие из палитры Matrix, и конечный момент времени. Следует иметь в виду, что интервал между вычисляемыми друг за другом значениями функций должен обеспечивать плавность изменения графика. На правом графике приведены те же параметры, но при шаге вычислений в 25 раз большем, чем на левом. Неправильный выбор шага может полностью исказить картину процесса.

Р ис. 18. Примеры построения графиков при монотонно изменяющемся аргументе.