2. Способы расчета дисперсии

Выбор способа расчета дисперсии зависит от того, в каком виде представлены исходные данные для ее расчета.

1. Расчет дисперсии в дискретных (не взвешенных) вариационных рядах осуществляется следующим образом:

. (1.9)

2. Расчет дисперсии в дискретных взвешенных вариационных рядах осуществляется следующим образом:

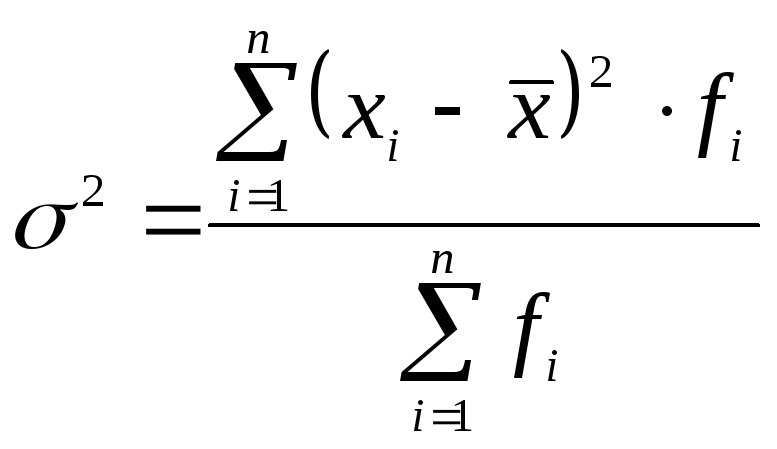. (1.10)

3. Расчет дисперсии в интервальных вариационных рядах осуществляется следующим образом:

- первый вариант:

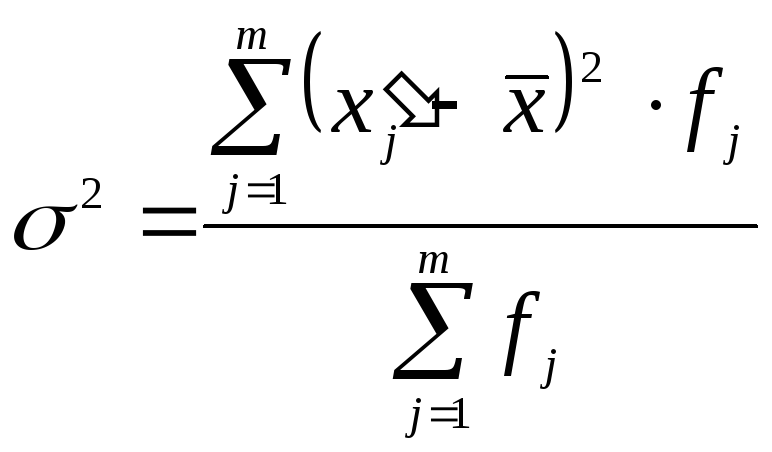. (1.11)

- второй вариант. При больших значениях вариантов и частот техника вычисления дисперсии по формуле (1.11) может быть громоздкой. Расчеты можно упростить, используя следующие свойства дисперсии:

1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз (N) дисперсии не изменяет;

1. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину (А) дисперсии не изменяет;

1. Уменьшение или увеличение каждого значения признака в k раз соответственно уменьшает или увеличивает дисперсию в 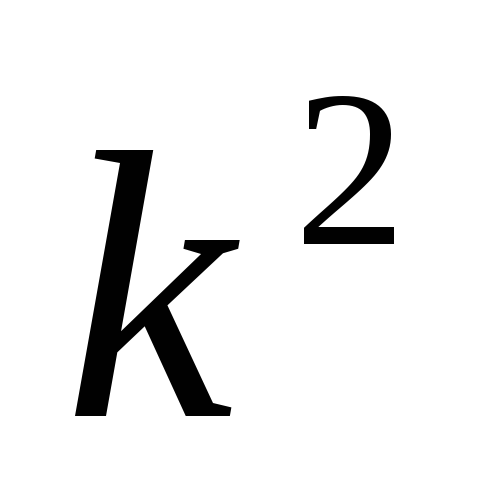раз.

Таким образом, при больших значениях варьирующего признака и частот, расчет дисперсии в интервальных рядах можно упростить, используя способ моментов:

, (1.12)

где h – величина интервала;

x^*_j – преобразованные значения вариантов:

, (1.13)

где А – постоянная величина, в качестве которой удобно выбрать середину интервала с наибольшей частотой;

; (1.14)

. (1.15)

4. Нахождение дисперсии альтернативного признака

Альтернативный признак – это признак, которым единицы изучаемой совокупности могут либо обладать, либо не обладать.

В таких случаях наличие признака обозначается единицей (1), а его отсутствие – нулем (0). Доля единиц, обладающих интересующим признаком, обозначается (p), доля остальных единиц – (q).

Средняя величина альтернативного признака определяется следующим образом:

(1.16)

Средняя альтернативного признака равна его доле в совокупности.

Дисперсия альтернативного признака:

.

Максимальное значение дисперсии альтернативного признака составляет 0,25 (при р = 0,5).

5. Если статистическая совокупность разбита на группы по какому-либо признаку, то средняя величина и дисперсия могут быть определены не только для всей совокупности, но и для каждой из составляющих ее групп.

Среднее значение признака в группе (групповая средняя) определяется по следующей формуле:

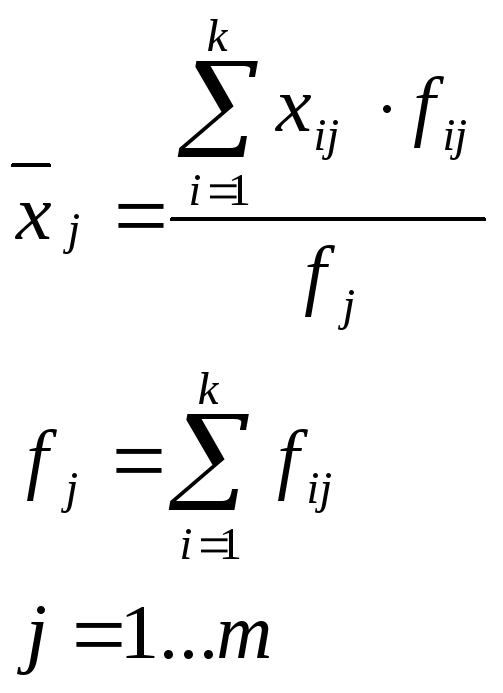, (1.17)

где – среднее значение признака в j-той группе (групповая средняя);

– вес j-той группы во всей совокупности;

– значение i-го вариационного признака в j-той группе;

f_ij – вес i–того значения признака в j–той группе;

k – число значений признака в j–той группе;

m – число групп на которые разбита совокупность.

Дисперсия признака в группе (групповая дисперсия).

Групповая (частная) дисперсия отражает вариацию признака за счёт условий и причин, действующих внутри группы, и определяется по формуле:

, (1.18)

где -групповая дисперсия j-той группы вариационного признака.

Среднее значение дисперсии по группе (средняя арифметическая взвешенная из групповых дисперсий) можно рассчитать следующим образом:

. (1.19)

Межгрупповая дисперсия характеризует колеблемость групповых средних около общей средней по совокупности и м. б. рассчитана по формуле:

, (1.20)

где – межгрупповая дисперсия;

– среднее значение вариационного признака для всей совокупности.

В математической статистике доказано, что общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии. Это называется правилом сложения дисперсий:

. (1.21)