Достаточное условие экстремума.

Если в стационарной точке P₀(x₀, y₀)

то эта точка является точкой экстремума функции f(x, y). Эта точка является точкой максимума, если

П р и м е р .z = 2 + 2x + 4y – x² – y².

В точка P₀(1, 2) - точка максимума. z_max= 7.

z z z = 7 – (x – 2)² + (y – 2)².

z₁

y

y₁

x₁ P₀

x

Уравнения кривой в пространстве.

Рассмотрим точку М(x, y, z) и вектор ОМ = r − радиус-вектор точки М.

r = x i + y j + z k (1)

z

M(x, y, z)

r

y

x

Пусть координаты вектора r есть функции некоторой переменной t

x = x(t), y = y(t), z = z(t) (2)

Тогда формулу (1) можно записать в виде

r (t) = x(t) i + y(t) j + z (t) k (1*)

или коротко

r = r(t).

Если t изменяется в некотором интервале t₁ ≤ t ≤ T, то точка М опишет некоторую кривую, которая называется годографом вектора r.

Уравнение (1*) называют векторным уравнением кривой в пространстве Уравнения (2) называют параметрическими уравнениями кривой, t – параметр.

Производная вектор-функции скалярного аргумента. Уравнения касательной к кривой в пространстве.

Рассмотрим формулу (1*). при изменении t вектор r изменяется по величине и по направлению. Говорят, что вектор r есть векторная функция скалярного аргумента t. Найдем далее производную векторной функции r(t). Уравнение (1*) определяет кривую в пространстве. Возьмем значение t = t₀, которому соответствует точка М(x₀, y₀, z₀) на кривой. Дадим t₀ приращение Δt и рассмотрим вектор

r(t₀ + Δt) = x(t₀ + Δt) i + y(t₀ + Δt) j + z(t₀+ Δt) k,

которому соответствует точка на кривой М₁(x₀ + Δx, y₀+ Δy, z₀ + Δz).

z T

M₁(x₀ + Δx, y₀ + Δy, z₀ + Δz)

Δr

M r(t + Δt)

r(t)

y

x

Рассмотрим вектор Δr = r(t₀ + Δt) – r(t₀) = {Δx, Δy, Δz} – направляющий вектор секущей ММ₁. Возьмем далее вектор , коллинеарный вектору Δr и найдем

Этот вектор обозначим и назовем производной от вектора r(t) по скалярному аргументу t.

Выясним направление вектора . Если Δt → 0, то точка М₁ по кривой стремится к точке М. Секущая ММ₁ стремится занять положение касательной МТ. Следовательно, есть направляющий вектор касательной к кривой. Уравнения касательной запишутся

П р и м е р .

Написать уравнения касательной к винтовой линии x = a cos t, y = a sin t, z = amt при t₀ = ^π /₄.

y

x

Касательная плоскость и нормаль к поверхности.

n

M₀

(L)

Рассмотрим поверхность F(x, y, z) = 0 и точку М₀(x₀, y₀, z₀). Пусть F′_x, F_y , F′_z точке М₀ существуют и непрерывны и не обращаются в нуль одновременно. Прямая называется касательной к поверхности, если она является касательной к какой-либо кривой, целиком лежащей на поверхности.

Докажем, что все касательный прямые к поверхности, проведенные в точке М₀, лежат в одной плоскости. Пусть

x = x(t), y = y(t), z = z(t)

– параметрические уравнения кривой (L), лежащей на поверхности. Пусть t₀ – значение параметра, соответствующего точке М₀.

s₀ = {x′(t₀), y(t₀), z′(t₀)}

– направляющий вектор касательной прямой к кривой (L). Тогда

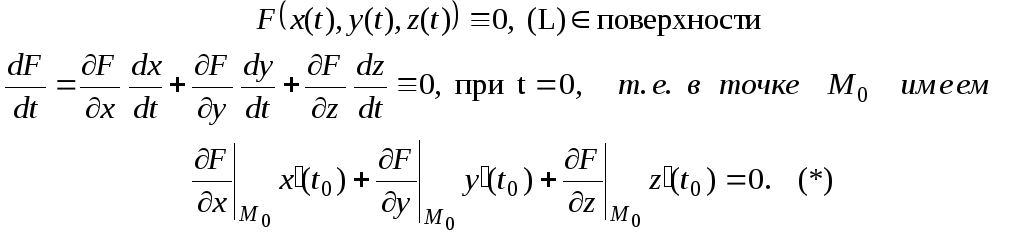
Рассмотрим вектор n = . Этот вектор не зависит от выбора кривой (L), а зависит только от поверхности и от точки М₀. Соотношение (*) означает, что скалярное произведение (n, s) = 0. Это означает, что все касательные прямые к поверхности, проведенные в точке М₀, перпендикулярны к одному и тому же вектору. Следовательно, они лежат в одной плоскости, которая называется касательной плоскостью к поверхности.

Уравнение касательной плоскости запишется в виде

. (**)

Прямая, проходящая через точку М₀ и перпендикулярная касательной плоскости, называется нормалью к поверхности.

− канонические уравнения нормали к поверхности.

Пусть поверхность задана уравнением z = f(x, y). Тогда

Уравнение касательной плоскости запишется

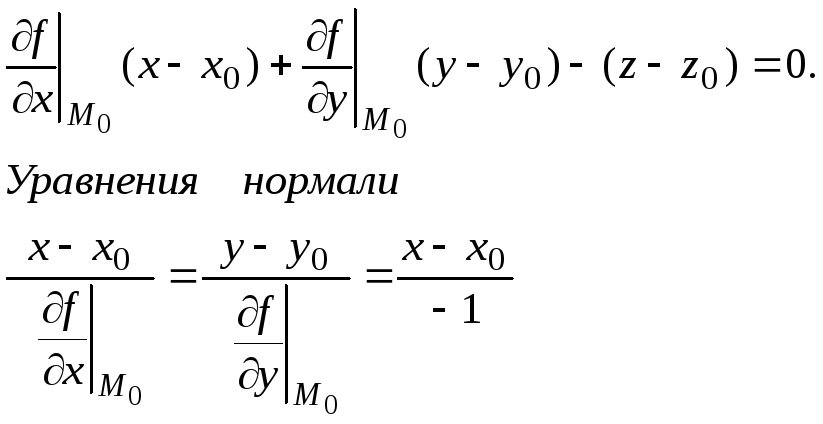
П р и м е р . Написать уравнение касательной плоскости к поверхности x² + y² + z² = 3 в точке М₀(1, 1, -1).

z

y

Mm

x n

Уравнение касательной плоскости имеет вид