Дифференцирование сложных функций.

Рассмотрим функцию z = F(u, v) и предположим, что u = φ(x, y), v = ψ(x, y). В этом случае z является сложной функцией от x и y. Найдем предполагая, что функции F(u, v), φ(x, y) и ψ(x, y) имеют непрерывные частные производные по всем аргументам. Дадим х приращение Δx. Тогда u и v получат приращения Δ_xu, Δ_xv, z получит приращение Δz.

Эти формулы обобщаются на случай большего числа переменных.

Рассмотрим z =f(t, x, y) и пусть x = x(t), y = y(t). Тогда является функцией от одной переменной t.

Производная неявной функции.

Рассмотрим неразрешенное относительно z уравнение

F(x,y,z) = 0 (*)

Это уравнение определяет z как неявную функцию относительно x и y z = z(x, y). Найдем Зафиксируем y и продифференцируем (*) по x, учитывая, что z зависит от х (по правилу дифференцирования сложной функции).

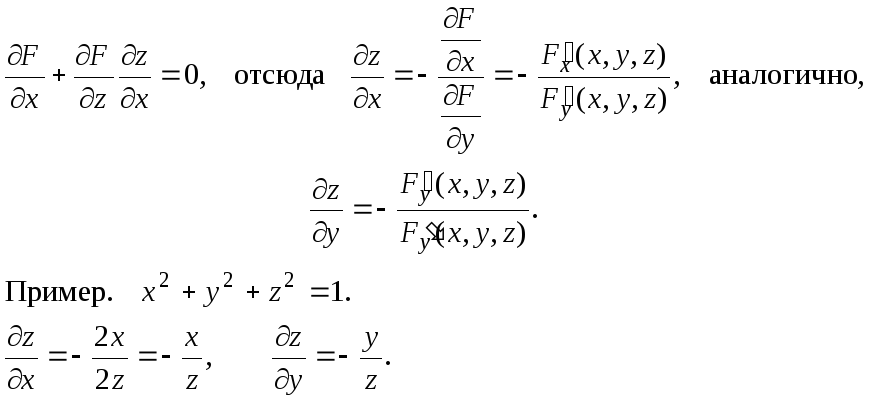
Формула Тейлора.

Для функции одной переменной имеем

Рассмотрим функцию f(x, y). Положим x = a + t Δx, y = b + t Δy. Здесь a, b, Δx и Δy – фиксированные значения, t – переменная величина. Тогда функция f(a + t Δx, b + t Δy) становится функцией только одной переменной t . Формула Тейлора для нее принимает вид (n = 2)

Дифференциал второго порядка.

- полный дифференциал первого порядка.

d(dz) =d²z – дифференциал второго порядка.

d²z = - дифференциал второго порядка от функции двух переменных z = f (x, y)/

Повторное дифференцирование.

Рассмотрим функцию z = f(x, y). Найдем

От этих производных можно также найти производные

Аналогично находятся производные более высоких порядков.

Например, z = x³ – 4x²y + 5y²,

Теорема.Если функция z = f(x, y) и ее частные

производные f′_x , f′_y, f′′_xy, f′′_yx непрерывны в точке (х,у)

то

Из этой теоремы вытекает, что

Экстремум функции двух переменных.

О п р е де л е н и е 1. Функция z = f(x, y) имеет максимум в точке M₀(x₀, y₀), (т.е. при x = x_0, y = y₀), если

f(x₀, y₀) > f(x, y)

для всех точек (x, y), достаточно близких к точке (x_0, y₀).

z

,

f(x₀,y₀) f(x,y)

y

(x,y)

x (x₀,y₀)

О п р е де л е н и е 2. Функция z = f(x, y) имеет минимум в точке M₀(x₀, y₀), (т.е. при x = x_0, y = y₀), если

f(x₀, y₀) < f(x, y)

для всех точек (x, y), достаточно близких к точке (x_0, y₀).

Z

f(x,y) f(x₀,y₀)

y

x

П р и м е р . z = x² + y². Точка x = y = 0 – точка минимума, т.к. в этой точке z = 0, и z > 0 при всех x ≠ 0 , y ≠ 0 .

Теорема (необходимое условие экстремума).

Если функция y = f(x, y) имеет экстремум при x = x₀, y = y₀, то ее частные производные первого порядка в этой точке либо равны нулю, либо не существуют.

Пусть в точке P₀(x₀, y₀) функция z = f(x, y) имеет

максимум. Зафиксируем y = y₀ и рассмотрим

z = f(x, y₀). Это функция одной переменной и у нее

точка x = x₀ является точкой максимума.

y₀ y Следовательно, f′_x(x₀, y₀) либо равна нулю, либо не

x₀ существует.

x P₀

Зафиксируем x = x₀ и рассмотрим z = f(x₀, y). Точка y = y₀ является точкой максимума. Следовательно, f′_y(x₀, y₀) либо равна нулю, либо не существует.

Это условие является только необходимым, но не является достаточным.

П р и м е р . z = x y. z′_x= y, z′_y = x. Очевидно, z′_x= z′_y = 0 при x = y = 0. При этом z = 0.

Но в любой окрестности точки (0, 0) z > 0, если x и y

y одного знака и z < 0, еcли x и y разных знаков.

Следовательно, в точке (0, 0) экстремума нет.

--

x